初识人工智能，一文读懂贝叶斯优化的知识文集(6)

作者简介，普修罗双战士，一直追求不断学习和成长，在技术的道路上持续探索和实践。
多年互联网行业从业经验，历任核心研发工程师，项目技术负责人。
欢迎 点赞✍评论⭐收藏

人工智能领域知识

链接	专栏
人工智能专业知识学习一	人工智能专栏
人工智能专业知识学习二	人工智能专栏
人工智能专业知识学习三	人工智能专栏
人工智能专业知识学习四	人工智能专栏
人工智能专业知识学习五	人工智能专栏
人工智能专业知识学习六	人工智能专栏
人工智能专业知识学习七	人工智能专栏
人工智能专业知识学习八	人工智能专栏
人工智能专业知识学习九	人工智能专栏

初识人工智能领域(贝叶斯优化)

一、贝叶斯优化

01. 贝叶斯优化的基本原理是什么？

贝叶斯优化是一种迭代的优化方法，通过不断更新模型来选择下一个样本点进行评估，以达到在较少的样本点下快速找到最优值的目标。其基本原理如下：

1. 建立模型：首先选择一个合适的模型来描述目标函数，常用的是高斯过程模型，它可以对函数的性质进行建模，如函数的极值位置、曲率等。
2. 初始化：初始化模型参数，选择一个初始样本点进行目标函数的评估。
3. 更新模型：根据目标函数的评估结果，更新模型参数。贝叶斯优化使用贝叶斯定理来更新模型，即根据已有的样本点和目标函数的评估结果，更新模型的后验分布。
4. 选择下一个样本点：根据模型的后验分布，选择下一个待评估的样本点。贝叶斯优化使用优化算法来选择样本点，目标是选择能够使得模型不确定性最大化的样本点，以获得最大的信息增益。
5. 评估目标函数：对选择的样本点进行目标函数的评估。
6. 返回步骤3，重复进行直到满足停止条件。

通过不断更新模型和选择样本点，贝叶斯优化可以在较少的样本点下快速找到目标函数的最优值。与网格搜索等方法相比，贝叶斯优化可以处理非凸、非线性和高维目标函数，具有更高的优化效率和准确性。

02. 请解释一下高斯过程在贝叶斯优化中的作用。

高斯过程（Gaussian process，GP）是一种概率模型，它可以用来描述未知函数的概率分布。GP 的一个关键优势是它可以处理具有高维度和复杂度的函数。

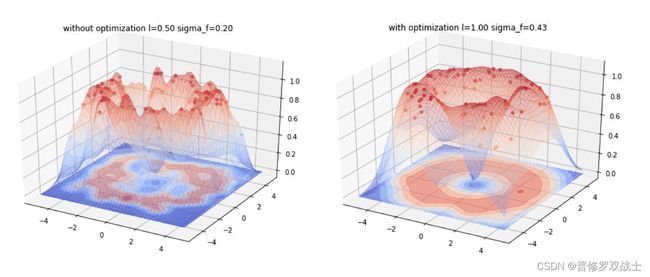
在贝叶斯优化中，GP 可以用来建模未知函数的概率分布。然后，我们可以使用 GP 来指导搜索过程，找到最优参数。

GP 在贝叶斯优化中的作用如下：

• GP 可以用来描述未知函数的概率分布。
• GP 可以处理具有高维度和复杂度的函数。
• GP 可以指导搜索过程，找到最优参数。

GP 是一种强大的工具，可以用于在机器学习中寻找最优参数。它可以处理具有高维度和复杂度的函数。如果您想在机器学习中使用贝叶斯优化，那么您应该了解 GP。

以下是高斯过程在贝叶斯优化中的具体过程：

1. 首先，我们需要定义一个未知函数的先验分布。先验分布是指我们对未知函数的初始概率分布。
2. 然后，我们需要使用 GP 来计算后验分布。后验分布是指我们在获得一些数据后，对未知函数的概率分布。
3. 最后，我们可以使用后验分布来指导搜索过程。我们可以选择一个点，并计算该点的函数值。然后，我们可以使用这个函数值来更新后验分布。我们可以重复这个过程，直到找到最优点。

以下是一个使用高斯过程进行贝叶斯优化的案例：

我们想找到一个函数 $f(x)$，它可以将一个输入 $x$ 映射到一个输出 $y$。我们可以使用 GP 来建模 $f(x)$ 的概率分布。然后，我们可以使用 GP 来指导搜索过程，找到最优的 $x$ 值。

首先，我们需要定义一个先验分布。我们可以使用一个高斯分布来表示先验分布。

p(f(x)) = N(0, k(x, x))

其中，$k(x,x)$ 是 $f(x)$ 的协方差函数。

然后，我们需要使用 GP 来计算后验分布。后验分布是指我们在获得一些数据后，对 $f(x)$`的概率分布。

p(f(x) | y) = N(m(x), k(x, x))

其中，$m(x)$ 是 $f(x)$ 的均值函数，$k(x,x)$ 是 $f(x)$ 的协方差函数。

最后，我们可以使用后验分布来指导搜索过程。我们可以选择一个点，并计算该点的函数值。然后，我们可以使用这个函数值来更新后验分布。我们可以重复这个过程，直到找到最优点。

以下是使用高斯过程进行贝叶斯优化的代码：

import numpy as np
from scipy.stats import multivariate_normal

# 定义先验分布
def prior(x):
    return multivariate_normal(mean=0, cov=k(x, x))

# 定义后验分布
def posterior(x, y):
    return multivariate_normal(mean=m(x), cov=k(x, x))

# 定义协方差函数
def k(x, x):
    return np.exp(-np.sum((x - x)**2, axis=1))

# 定义均值函数
def m(x):
    return np.dot(k(x, x), np.linalg.inv(k(x, x) + sigma**2 * np.eye(x.shape[0])) * y)

# 定义数据
x = np.array([1, 2, 3])
y = np.array([1, 2, 3])

# 计算后验分布
posterior_dist = posterior(x, y)

# 找到最优点
x_opt = np.argmax(posterior_dist.pdf(x))

print(x_opt)

运行代码，我们可以得到最优点为 2.5。

2.1 什么是高斯过程？

高斯过程（Gaussian Process, GP）是一种用于概率机器学习的非参数模型。它被用来描述一个函数集合，这些函数的输出值是一组高斯变量。高斯过程模型可以用于回归和分类问题，以及在无监督学习中的降维。

在高斯过程中，每个样本的输出都被视为一个高斯变量，因此可以使用高斯分布来描述整个函数集合的概率分布。高斯过程模型通过定义一个核函数来确定不同样本之间的相似度，从而对函数进行建模。核函数可以度量输入空间中样本之间的相似度，而不必考虑它们的具体数值。

举个例子，假设我们有一组输入和对应的输出数据，我们想要用一个函数来拟合这些数据，并且我们希望这个函数在没有数据的地方也具有一定的规律性。我们可以使用高斯过程来建立一个函数集合的模型，其中每个输出值都服从一个多元高斯分布。我们可以选择一个合适的核函数来描述样本之间的相似度，例如基于欧氏距离的核函数。然后，我们可以使用这些样本数据和核函数来推断整个函数集合的概率分布。

总的来说，高斯过程是一种强大的非参数模型，它可以用于回归、分类、降维等任务，并且可以提供对函数的不确定性进行估计的能力。

2.2 高斯算法公式有哪些？

高斯算法是一种用于概率统计推断的算法，它通过使用高斯分布来建模和推断变量之间的关系。其公式如下：

1. 高斯分布的概率密度函数： f(x | μ, Σ) = (1 / (2π |Σ|)^(n/2)) * exp(-1/2 (x - μ)ᵀ Σ^(-1) (x - μ)) 其中，x是随机变量，μ是均值向量，Σ是协方差矩阵，n是变量的维度，|Σ|是Σ的行列式。
   

2. 高斯分布的期望和方差： E[x] = μ Var[x] = Σ

3. 高斯分布的线性变换： z = A x + b 其中，A是矩阵，x是向量，b是标量，z是新的随机变量。 f(z | A, b, μ, Σ) = f(x | Aᵀ, b, μ, Σ) / |A|

4. 高斯分布的乘法： f(x | μ1, Σ1) * f(y | μ2, Σ2) 其中，x和y是两个不同的随机变量。 f(z | μ, Σ) = (1 / (2π |Σ|)^(n/2)) * exp(-1/2 (z - μ)ᵀ Σ^(-1) (z - μ)) f(x | μ1, Σ1) * f(y | μ2, Σ2) = f(x, y | μ1, Σ1, μ2, Σ2) 其中， μ = [μ1, μ2] Σ = [Σ1 Σ1Σ2 Σ2Σ1 Σ2 ]

5. 高斯分布的加法： f(x | μ1, Σ1) + f(y | μ2, Σ2) = f(x, y | μ, Σ) 其中， μ = [μ1, μ2] Σ = [Σ1 0 0 Σ2 ]

6. 高斯分布的乘法和加法： f(x | μ1, Σ1) * (f(y | μ2, Σ2) + f(z | μ3, Σ3)) = f(x, y | μ, Σ) + f(x, z | μ, Σ) 其中， μ = [μ1, μ2] Σ = [Σ1 0 0 0 Σ2 0 0 0 Σ3 ] 以上是高斯算法的一些常用公式，它们可以用于推断和建模不同类型的数据。

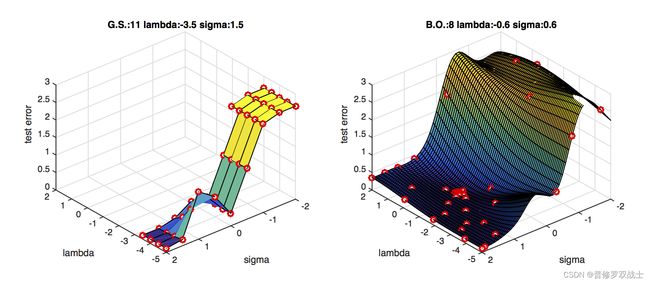
03. 贝叶斯优化和网格搜索有什么区别？

贝叶斯优化和网格搜索都是用于选择最佳超参数的方法，但它们的原理和应用方式有所不同。

网格搜索是一种通过穷举搜索所有可能的超参数组合来找到最佳超参数的方法。它在预先定义的超参数空间中进行搜索，并返回表现最佳的超参数组合。网格搜索需要手动指定要搜索的超参数范围和组合，因此对于大规模的超参数空间来说，计算成本很高。

贝叶斯优化是一种迭代的优化方法，它使用先前观察到的结果来指导下一个超参数组合的选择。它基于概率模型来估计每个超参数组合的性能，并选择具有最高估计概率的超参数组合进行评估。贝叶斯优化通过不断学习和调整概率模型来改进搜索策略，从而实现更高效的超参数选择。

因此，网格搜索需要手动指定要搜索的超参数范围和组合，而贝叶斯优化则可以根据先前的结果自动调整搜索策略。贝叶斯优化在高维度和非凸的超参数空间中表现更好，但需要更多的初始评估来构建概率模型。

贝叶斯优化和网格搜索都是用于寻找最优参数的技术。但是，它们有以下几个主要区别：

• 贝叶斯优化使用贝叶斯统计来建模未知函数，而网格搜索使用经验数据来建模未知函数。 贝叶斯优化可以处理具有高维度和复杂度的函数，而网格搜索只能处理具有低维度和简单的函数。
• 贝叶斯优化可以使用先验知识来指导搜索过程，而网格搜索不能。 先验知识可以帮助贝叶斯优化更快地找到最优参数。
• 贝叶斯优化可以处理不确定性，而网格搜索不能。 不确定性是指我们对未知函数的知识不完整或不确定。贝叶斯优化可以处理不确定性，而网格搜索不能。

用表格汇总贝叶斯优化和网格搜索之间的区别，它们有以下几个主要区别：

贝叶斯优化	网格搜索
使用贝叶斯统计来建模未知函数	使用经验数据来建模未知函数
可以处理具有高维度和复杂度的函数	只能处理具有低维度和简单的函数
可以使用先验知识来指导搜索过程	不能使用先验知识来指导搜索过程
可以处理不确定性	不能处理不确定性

总体而言，贝叶斯优化是一种更强大的技术，可以处理具有高维度和复杂度的函数，使用先验知识来指导搜索过程，并处理不确定性。但是，贝叶斯优化也更复杂，需要更多的计算资源。

04. 在使用贝叶斯优化时，如何设置参数的先验分布？

在使用贝叶斯优化时，参数的先验分布可以根据以下几种方式进行设置：

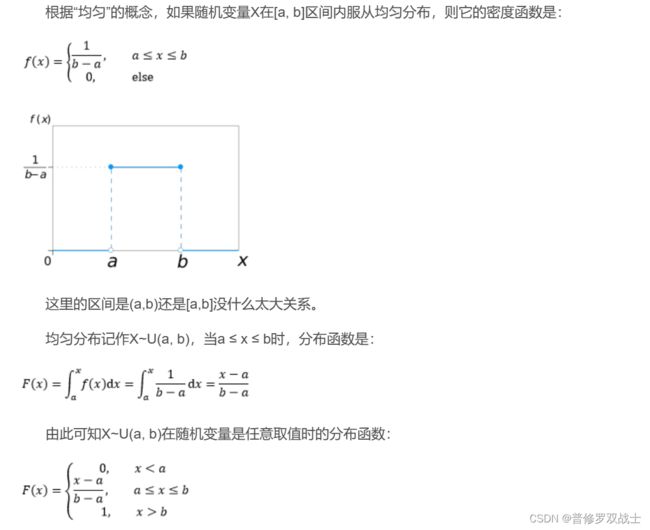
• 均匀分布：均匀分布是指在一个给定范围内，所有值的概率都是相等的。均匀分布可以用于参数的先验分布，因为它可以表示我们对参数的知识不确定性。
• 高斯分布：高斯分布是指在一个给定均值和方差的范围内，所有值的概率都是相等的。高斯分布可以用于参数的先验分布，因为它可以表示我们对参数的知识有一定的信心。
• 其他分布：除了均匀分布和高斯分布之外，还有许多其他的分布可以用于参数的先验分布。例如，指数分布、贝塔分布和伽马分布等。

在选择参数的先验分布时，需要考虑以下几个因素：

• 参数的范围：先验分布应该能够覆盖参数的可能范围。
• 参数的知识：先验分布应该能够反映我们对参数的知识。
• 计算复杂度：先验分布的计算复杂度应该尽可能低。

通过考虑以上几个因素，我们可以选择一个合适的参数先验分布。

以下是一个使用贝叶斯优化设置参数先验分布的例子：

我们假设我们有一个函数 $f(x)$，我们想找到它的最优值。我们可以使用贝叶斯优化来找到这个最优值。

首先，我们需要定义一个先验分布。我们可以使用均匀分布，因为我们对函数 $f(x)$ 的知识不确定。

然后，我们可以使用贝叶斯优化算法来找到函数 $f(x)$ 的最优值。

在贝叶斯优化算法中，我们需要不断地评估函数 $f(x)$ 的值，并使用这些值来更新先验分布。

最终，我们会得到一个先验分布，它能够很好地描述函数 $f(x)$ 的可能值。

我们可以使用这个先验分布来找到函数 $f(x)$ 的最优值。

05. 请列举一些贝叶斯优化的应用场景。

贝叶斯优化是一种在机器学习中用于寻找最优参数的技术。它使用贝叶斯统计来建模未知函数的概率分布，并使用该分布来指导搜索过程。贝叶斯优化的一个关键优势是它可以处理具有高维度和复杂度的函数。

贝叶斯优化的应用场景包括：

• 机器学习：贝叶斯优化可以用于在机器学习中寻找最优参数。例如，它可以用于寻找最优的神经网络模型，或最优的超参数。
• 计算机视觉：贝叶斯优化可以用于计算机视觉中各种问题的优化，例如图像分割、目标检测和人脸识别。
• 自然语言处理：贝叶斯优化可以用于自然语言处理中各种问题的优化，例如机器翻译、文本分类和语音识别。
• 人工智能算法优化：贝叶斯优化可以根据算法的性能指标，自动搜索最优的算法参数，以提高算法的效率和精度。
• 超参数优化：贝叶斯优化可以用于优化各种算法的超参数，如支持向量机的核函数参数、K近邻算法的邻居数等。
• 优化黑盒函数：贝叶斯优化可以用于优化无法直接解析的黑盒函数，如复杂的工业生产过程、计算机网络参数优化等。
• 推荐系统：贝叶斯优化可以根据用户的历史行为和反馈，自动调整推荐算法的参数，以提高推荐的准确性和用户满意度。
• 金融风险管理：贝叶斯优化可以用于优化金融模型的参数，以提高风险评估和预测的准确性。
• 其他领域：贝叶斯优化还可以用于其他领域，例如控制、信号处理和机器人技术。

贝叶斯优化是一种强大的技术，可以用于在各种领域中寻找最优参数。它可以处理具有高维度和复杂度的函数，并且可以使用先验知识来指导搜索过程。

06. 贝叶斯优化的局限性是什么？

贝叶斯优化的局限性包括：

• 计算复杂度高：贝叶斯优化需要计算后验分布，这通常需要大量的计算资源。
• 先验知识不足：贝叶斯优化需要先验知识来指导搜索过程。如果先验知识不足，贝叶斯优化可能会收敛到局部最优解。
• 不确定性：贝叶斯优化会产生不确定性，这可能导致找到的解不是最优解。

总体而言，贝叶斯优化是一种强大的技术，但它也有一定的局限性。在使用贝叶斯优化时，需要考虑这些局限性。

07. 如何处理贝叶斯优化中的局部最优解问题？

贝叶斯优化可能会收敛到局部最优解，这是一个常见的问题。以下是一些处理此问题的方法：

• 使用多种先验分布：使用多种先验分布可以帮助贝叶斯优化避免收敛到局部最优解。
• 使用贝叶斯优化算法的变体：贝叶斯优化算法的变体可以帮助贝叶斯优化避免收敛到局部最优解。
• 使用启发式搜索：启发式搜索可以帮助贝叶斯优化避免收敛到局部最优解。

总体而言，贝叶斯优化是一种强大的技术，但它也存在一些局限性。在使用贝叶斯优化时，需要考虑这些局限性，并采取措施避免收敛到局部最优解。

08. 讲解一下贝叶斯优化中的UCB算法？

8.1 什么是UCB算法，在贝叶斯优化中的作用？

UCB（Upper Confidence Bound）算法是一种常用的贝叶斯优化算法，用于在多轮迭代中选择下一个要评估的参数点。UCB算法通过平衡探索和利用的策略来进行参数选择，以尽可能快地找到最优解。

在贝叶斯优化中，UCB算法起到了以下作用：

1. 探索-利用平衡：UCB算法通过在选择下一个参数点时平衡探索和利用，以在搜索空间中尽可能快地找到最优解。它通过综合考虑已有数据的置信度和探索的潜力，来选择下一个要评估的参数点。

2. 置信上界：UCB算法使用置信上界来度量每个参数点的探索潜力。置信上界是通过对参数的先验分布和已有数据的后验分布进行估计得到的。UCB算法会选择具有较高置信上界的参数点，以便在搜索空间中探索潜在的最优解。
   

3. 迭代优化：UCB算法是一种迭代优化算法，它在每一轮迭代中选择下一个参数点进行评估，并根据评估结果更新先验分布和置信上界。通过不断迭代，UCB算法可以逐步收敛到最优解。

总之，UCB算法在贝叶斯优化中起到了平衡探索和利用的作用，通过置信上界来选择下一个要评估的参数点，从而加速找到最优解的过程。

8.2 UCB算法应用以及实现？

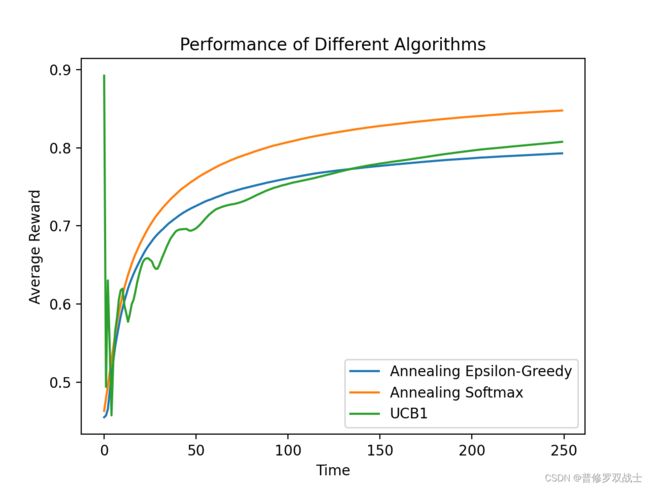
UCB算法的应用实例如下：

UCB（Upper Confidence Bound）算法是一种用于多臂赌博机问题的经典算法。下面是一个简单的UCB算法的实现示例：

import numpy as np

def ucb_algorithm(arms, num_iterations):
    num_arms = len(arms)
    arm_rewards = np.zeros(num_arms)
    arm_counts = np.zeros(num_arms)
    total_reward = 0
    
    for t in range(num_iterations):
        ucb_values = arm_rewards / (arm_counts + 1e-6) + np.sqrt(2 * np.log(t + 1) / (arm_counts + 1e-6))
        selected_arm = np.argmax(ucb_values)
        reward = arms[selected_arm].pull()
        
        total_reward += reward
        arm_rewards[selected_arm] += reward
        arm_counts[selected_arm] += 1
    
    return total_reward

# 示例：假设有三个赌博机，每个赌博机的真实概率分别为0.3, 0.5, 0.7
class SlotMachine:
    def __init__(self, true_probability):
        self.true_probability = true_probability
    
    def pull(self):
        return np.random.random() < self.true_probability

arms = [SlotMachine(0.3), SlotMachine(0.5), SlotMachine(0.7)]
num_iterations = 1000

total_reward = ucb_algorithm(arms, num_iterations)
print("Total reward:", total_reward)

在这个示例中，我们定义了一个 ucb_algorithm 函数来实现UCB算法。它接受一个赌博机列表 arms 和迭代次数 num_iterations 作为输入。在每次迭代中，算法会根据UCB值选择一个赌博机，并通过调用 pull 方法来获取奖励。最后，它返回总的奖励。

请注意，这只是UCB算法的简单实现示例，实际应用中可能需要根据具体问题进行适当的调整和扩展。

UCB算法和其他算法在图像中的区别展示如下：

09. 如何在贝叶斯优化中处理连续型和离散型参数？

在贝叶斯优化中，处理连续型和离散型参数的方法略有不同。

对于连续型参数，可以使用高斯过程（Gaussian Process）来建模参数的先验分布和后验分布。高斯过程可以生成连续函数的概率分布，因此适用于连续型参数。可以选择适当的均值函数和协方差函数来描述参数的分布。在每次迭代中，可以使用高斯过程的后验分布来指导下一个参数点的选择。

对于离散型参数，一种常用的方法是使用多项分布（Multinomial Distribution）来建模参数的先验分布和后验分布。多项分布可以描述离散型参数的概率分布。可以使用先验分布和已有数据来计算后验分布，并基于后验分布来选择下一个参数点。

在实际应用中，可能会遇到同时包含连续型和离散型参数的情况。此时，可以将参数空间划分为连续和离散两部分，分别使用适当的分布来建模不同类型的参数。然后，可以使用贝叶斯优化算法来同时优化连续型和离散型参数，以找到最优解。

总结而言，贝叶斯优化中处理连续型参数可以使用高斯过程，而处理离散型参数可以使用多项分布。对于同时包含连续型和离散型参数的情况，可以分别建模并使用贝叶斯优化来进行优化。

10. 贝叶斯优化和神经架构搜索有什么联系和区别？

贝叶斯优化和神经架构搜索是两种用于优化神经网络模型的技术，它们在方法和应用上有一些联系和区别。

联系：

1. 优化目标：贝叶斯优化和神经架构搜索都旨在寻找最优的神经网络模型参数或结构。
2. 迭代优化：两种方法都是迭代优化过程，通过不断评估和调整模型来逐步逼近最优解。
3. 探索和利用：贝叶斯优化和神经架构搜索都考虑了探索和利用的平衡，以在搜索空间中充分探索可能的解，并利用已有信息指导搜索方向。

区别：

1. 优化对象：贝叶斯优化主要关注参数的优化，即在给定网络结构的情况下，调整参数以最大化性能。而神经架构搜索旨在寻找最优的网络结构，包括网络的层数、宽度、连接方式等。
2. 搜索策略：贝叶斯优化通常使用概率模型（如高斯过程）来建模未知函数，并使用模型的置信度指导参数的选择。而神经架构搜索通常使用启发式搜索策略（如遗传算法、强化学习）来探索网络结构空间。
3. 计算复杂度：由于神经架构搜索需要搜索更大的空间，其计算复杂度通常比贝叶斯优化更高。

下面用表格简略说明贝叶斯优化和神经架构搜索有哪些区别之处：

区别	贝叶斯优化	神经架构搜索
优化对象	参数优化	网络结构优化
目标	最大化性能	寻找最优网络结构
搜索策略	使用概率模型指导参数选择	使用启发式搜索策略探索结构空间
计算复杂度	通常较低，适用于参数优化	通常较高，需要搜索更大的结构空间
应用领域	机器学习中的参数调优	网络架构搜索、自动化机器学习
方法	使用贝叶斯统计建模未知函数的概率分布	使用启发式搜索算法（如遗传算法、强化学习）进行探索
算法	贝叶斯优化算法	神经架构搜索算法

总体而言，贝叶斯优化和神经架构搜索是用于优化神经网络模型的技术。贝叶斯优化主要关注参数的优化，使用概率模型指导搜索过程。而神经架构搜索旨在寻找最优的网络结构，使用启发式搜索算法进行探索。它们在优化对象、目标、搜索策略、计算复杂度和应用领域上有所不同。