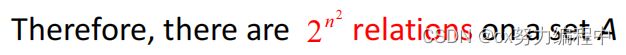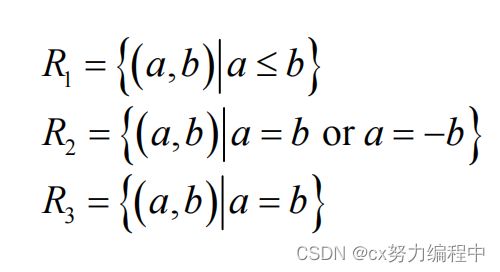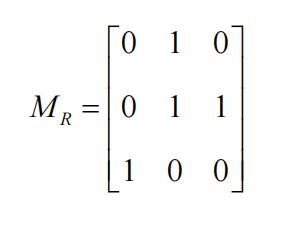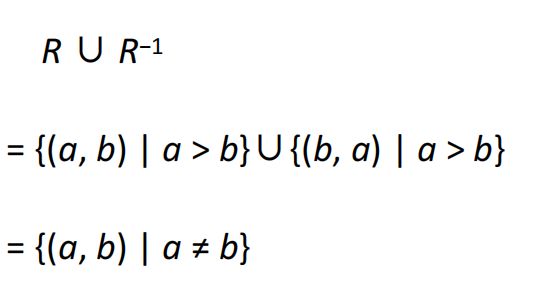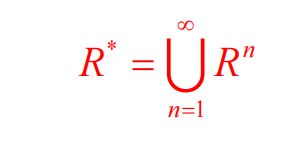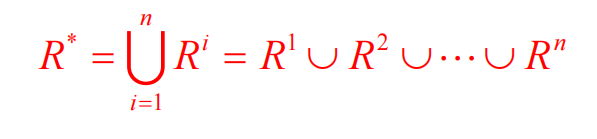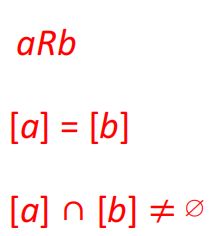离散数学期末复习(3):关系
目录
9.1 Relations and Their Properties (关系及其性质)
1.二元关系(binary relation)
(1)基本概念:
(2)自反(reflexive)
(3)对称(symmetric)
(4)反对称(antisymmetric)
编辑(5)传递性(transitive)
2.复合关系
9.3 Representing Relations (关系的表示)
1.矩阵如何表示关系
2.矩阵运算
(1)并集和交集
(2)矩阵复合
编辑 (3)复合矩阵的幂
3.图是怎么表示关系的
(1)有向图
(2)关系
9.4 Closures of Relations (关系的闭包)
1.定义:
编辑 2.自反闭包
3.对称闭包
4.路径(path)
5.传递闭包
9.5 Equivalence Relations (等价关系)
1.等价关系
2.字符串
3.等价关系的判断(从传递性,对称性,自反性三个方面考虑)
(1)同余模
(2)除法
4.等价类(Equivalence Classes)
(1)同余类(Congruence Classes)
(2)集合A的关系等价类的并集就是他自己
(3)集合的划分
9.6 Partial Orderings (偏序)
1.偏序的定义:
2.偏序集
3.字典排列
4.哈塞图(Hasse Diagrams)
(2)最大元素(maximal element(s))和最小元素(minimal element(s))
(3)最大最小元
(4)上下界
(5)最小上下界
(6)格(lattice)
(7)拓扑排序(Topological Sorting)
9.1 Relations and Their Properties (关系及其性质)
1.二元关系(binary relation)
(1)基本概念:
一个二元关系R是集合A到集合B的一个子集
集合A上的二进制关系就是A×A的子集和集合A到A的关系
那么集合A上面有多少关系呢?
因为A×A有n^2个元素,所以A×A有2^n^2个子集
(2)自反(reflexive)
设R是集合A上的一个关系, 如果对A中的每一个元素x, 均有(x, x) ∈ R, 则称R是自反关系,即 R是自反的 ⇔ ∀x(x∈A →x, x) ∈R).
例如:正整数集合上的整除关系 (正整数总能被自己整除), 相等关系等都是自反的关系。整数集合上的大于关系, 小于关系等都不是自反的关系。
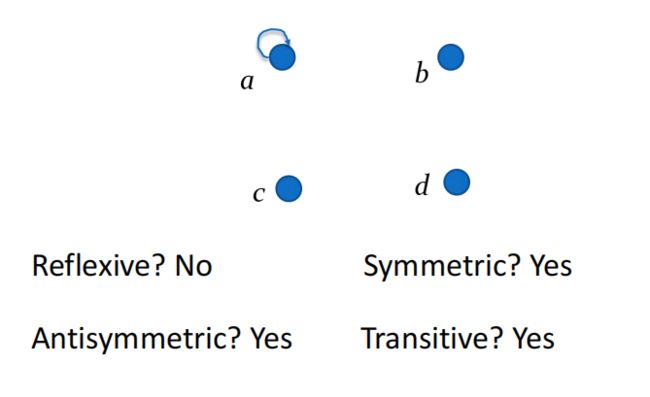
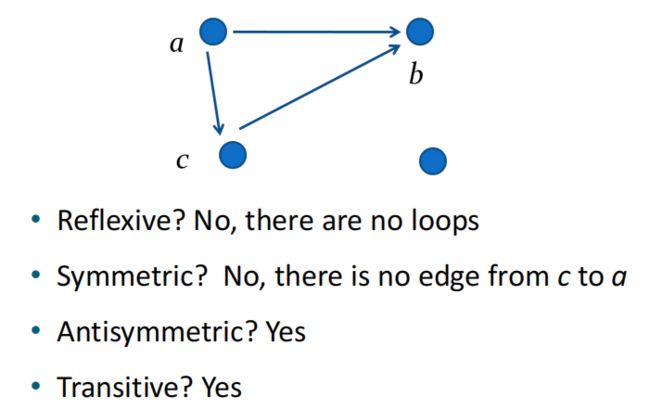
下面三个是自反关系的例子
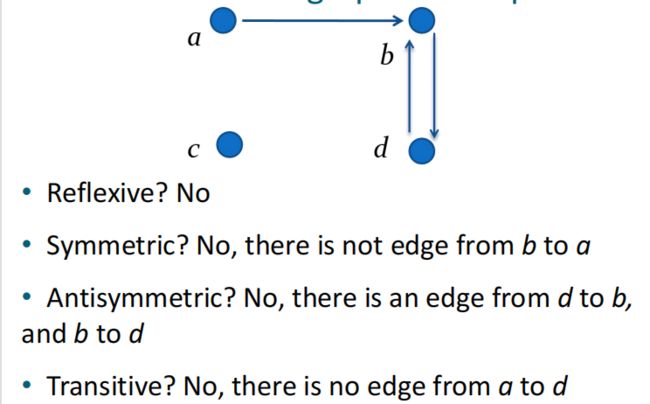
下面是三种情况不是自反
(3)对称(symmetric)
设R是集合A上的一个关系, 如果对A中的每一个元素x和元素y, 如有(x, y) ∈ R,必有(y, x)∈R, 则称R是对称关系,即 R是对称的 ⇔ ∀x∀y (x∈A ∧ y∈A ∧(x, y) ∈ R → (y, x) ∉ R)
例如:整数集合上的等于关系,任意集合上的全域关系, 同学关系,朋友关系等都是对称的。
(4)反对称(antisymmetric)

(5)传递性(transitive)
设R是集合A上的一个关系, x、y、z是A中的元素, 若(x, y) ∈ R 和 (y, z) ∈ R,
必有(x , z) ∈ R, 则称R是传递关系。
例如:实数集合上的大于关系, 小于关系都是传递关系,同学关系、朋友关系等不一定是传递的。
2.复合关系
R1是集合A到集合B的关系
R2是集合B到集合C的关系
R2和R1的复合关系 R2![]() R1 = 集合A到集合C的关系(有点传递的味道)
R1 = 集合A到集合C的关系(有点传递的味道)
关系的幂(用归纳法)
传递关系的幂是该关系的子集
9.3 Representing Relations (关系的表示)
1.矩阵如何表示关系
(1)有限集之间的关系可以用零1矩阵来表示
(2)A = {a1,a2,a3,...}
B = {b1,b2,b3,...}
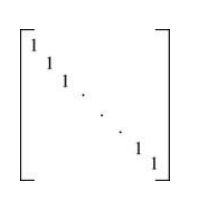
(3)如果R是自反关系,那矩阵里主对角线上的元素都是1
(4)如果R表示对称关系,那么MR是对称矩阵
如果R表示反对称关系,那么矩阵里i≠j时,mij = 0或者mji = 0
2.矩阵运算
(1)并集和交集
并集就是两个矩阵相同位置上的元素按照真值表进行析取(有至少一个1为1,同0为0)
交集就是两个矩阵相同位置上的元素按照真值表进行合取(有至少一个0为0,同1为1)
(2)矩阵复合
其实就是两个矩阵相乘(注意矩阵乘法的前提)
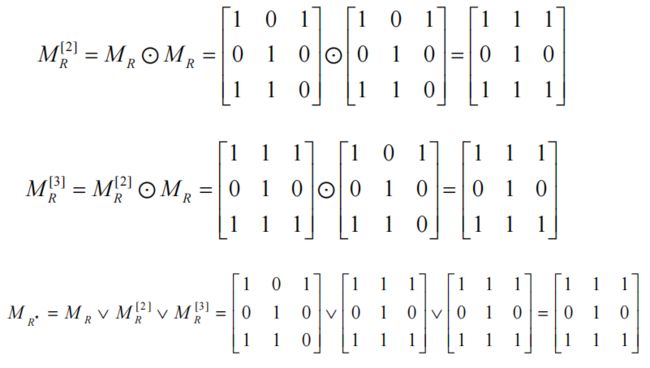
 (3)复合矩阵的幂
(3)复合矩阵的幂
3.图是怎么表示关系的
(1)有向图
一个有向图由一组顶点V(点,vertices)组成,以及一组被称为E, (边, edge)的有序元素对组成
顶点a称为边(a,b)的始点,顶点b称为该边的终点;边(a,a)称为环
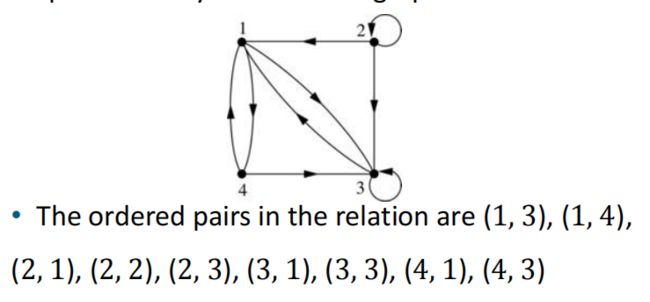
(2)关系
自反性:就是一个环绕着一个点
对称性:如果边(x, y)存在,那么(y, x)必须存在,必须存在双向边
反对称性:如果边(x, y)(x≠y)存在,那么边(y, x)不存在,只存在单项边
传递性:如果边(x,y)和(y, z)都存在,那么边(x, z)必须存在
如果条件(边(x,y)和(y, z))里面少了一条边,而且结果(边(x, y))也不存在,也就是说只有一条单向边(a指向b,但b不指向任何点),这种情况也满足传递性
在一幅图里面,如果找到一组或一条边不符合上面的性质,那这个图就没有对应的性质
9.4 Closures of Relations (关系的闭包)
1.定义:
 2.自反闭包
2.自反闭包
设 R = {(a, b) | a < b}是自然数集合上的一个关系
R的自反闭包为
3.对称闭包
R的对称闭包
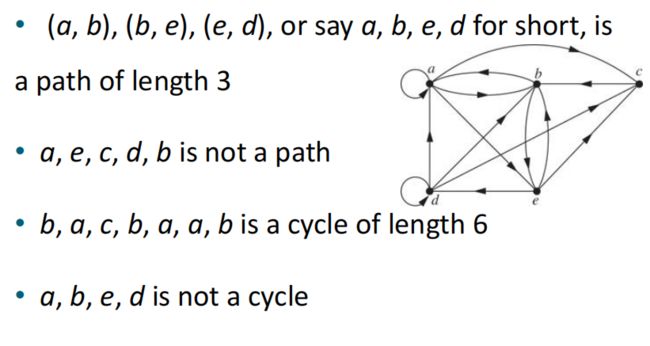
4.路径(path)
在有向图中,从a到b的路径是一组边的序列
比如(a,x1), (x1, x2), (x2, x3)等等
路径的长度就是路径的边的总数
(1)边集为空时,路径长度为0
(2)长度n-1,起点和重点都在同一位置的路径被称为圈
路径和边的关系:
(1)有向图中的一条路径可以多次通过一个顶点
(2)有向图中的一条边可以在一条路径中出现不止一次
5.传递闭包
(1)连通关系
连通关系R*由成对的路径(a,b)组成,指的是从a到b包含的n种走法,每种走法的路径大小至少为1.
Rn是路径(a,b)的集合,指的是从a到b的一条长度为n的路径
(2)传递闭包 = 连通关系R*
传递闭包的例子
用零1矩阵来表示传递闭包
9.5 Equivalence Relations (等价关系)
1.等价关系
如果一个集合上的关系是自反的、对称的、传递的,则称为等价关系
2.字符串
I(x)表示x 的字符串长度,当集合上的两个元素的字符串长度相等的时候(I(a) = I(b)),我们称a和b之间存在关系,写成aRb
自反性:I(a) = I(a),比如aRa
对称性:aRb,如果I(a) = I(b)成立,I(b) = I(a)也成立,我们可以得出bRa
传递性:假设有aRb和bRc。由于(a)=(b)和(a)=(c)都成立,我们可以得出aRc
3.等价关系的判断(从传递性,对称性,自反性三个方面考虑)
(1)同余模
(2)除法
4.等价类(Equivalence Classes)
与A的元素a相关的所有元素的集合称为a的等价类,在关系R上的等价类写成![]()
集合里两个元素等价可以表示成
(1)同余类(Congruence Classes)
一个整数a模m的同余类表示为
比如:
(2)集合A的关系等价类的并集就是他自己
(3)集合的划分
把集合分割成一块一块的
例子:
集合划分的等价类
9.6 Partial Orderings (偏序)
R是非空集合A上的关系,如果R是自反的,反对称的,和传递的,则称R是A上的偏序关系。(和等价关系的区分:等价关系有对称性,没有反对称;偏序有反对称,没有对称)
1.偏序的定义:
设R是集合A上的一个二元关系,若R满足:
Ⅰ 自反性:对任意x∈A,有xRx;
Ⅱ 反对称性(即反对称关系):对任意x,y∈A,若xRy,且yRx,则x=y;
Ⅲ 传递性:对任意x, y,z∈A,若xRy,且yRz,则xRz。 则称R为A上的偏序关系。
例子:证明“大于或等于”关系(≥)是在整数集合上的偏序
2.偏序集
集合S和偏序R组成偏序集,记作(S, R)
如果a≼b或b≼a,那么当a和b是偏序集(S,≼) 的元素时,那么a和b是可比的。
当a和b是(S,≼) 的元素,但是不满足a≼b和b≼a,那么a和b被称为不可比的。
(这里的≤可以替换成任何数学符号,如果偏序集里面的元素经过该符号运算之后数学逻辑结果存在,那就是可比的,反之不可比。)
例子:
如果S的每两个元素都具有可比性,那么S被称为全序集(totally ordered set)或线序集(linearly ordered set),≼被称为全序(total order)或线序。
一个全序集也被称为链。
偏序集(S,≼)中,≼是全序,并且S每个非空子集都有一个最小元素,那这个偏序集被称为良序集(well-ordered set)
3.字典排列
假设有两个偏序集(A1、≼1)和(A2、≼2),A1⨉A2上的字典排序通过指定(a1, a2)小于(b1, b2),即(a1, a2)≺(b1, b2)、a1≺![]() b1或a1=b1和a2≺
b1或a1=b1和a2≺![]() b2来定义
b2来定义
从两个集合第一个元素开始比较,小的排前面,相等就跳到下一个元素。
![]()
这里第三个元素3小于4,所以第一个个偏序集小于第二个, 只要找到大小关系,就不管后面元素的大小关系了
4.哈塞图(Hasse Diagrams)
(1)定义:
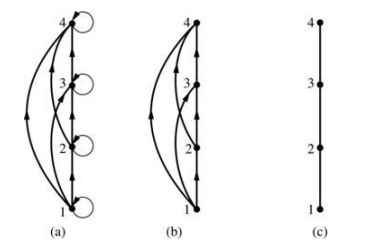
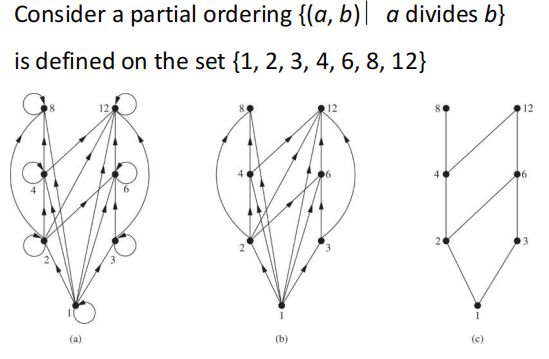
哈塞图是一种部分排序的视觉表示,它忽略了自反和传递性质所呈现的边
a图到b图,消除了自反留下的环;b图到c图,消除了传递产生的边
(2)最大元素(maximal element(s))和最小元素(minimal element(s))
最大元素就是画出的哈塞图最顶上(不再延伸出去)的那些元素,最小元素就是最底下的那些元素
(3)最大最小元
最大元(greatest element):在所有元素里面最大的元素(唯一)
最小元(least element):最小的元素(唯一)
a图有最小元,但是因为b,c,d地位相等,所以不存在最大元;
b图最大元素和最小元素各有两个,所以没有最大元和最小元
(4)上下界
设A是S的一个子集
上界(upper bound):u是S里的一个元素,而且S里面的所有元素都≤u, 这个u就是A的上界
下界(lower bound):a是S里的一个元素,而且S里面的所有元素都≥a, 这个a就是A的下界
(5)最小上下界
最小上界(least upper bound):在所有上界元素里面最小的元素(唯一)
最大下界(greatest lower bound):在所有下界元素里面最大的元素(唯一)
{b,d,g}的上界元素有g和h, 因为g小于h,所以g就是最小上界
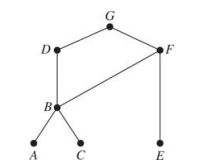
(6)格(lattice)
如果一个偏序集每一对元素都有最小上界,也有最大下界,那么这个偏序集称为格
(7)拓扑排序(Topological Sorting)
假设R是一个偏序,如果每当aRb都有a≼b,则说一个全序≼与偏序R兼容,从偏序构造一个兼容的全序的过程称为拓扑排序。
拓扑排序的步骤:
1.找出偏序集(A, ≤)的最小元素a1
2.把a1删除,接着在偏序(A − {a1 }, ≼ )找最小元素a2
3.删除a2,继续在偏序(A − {a1 , a2 }, ≼ )找最小元素a3
以此类推,直到A为空
例子:拓扑排序偏序({1, 2, 4, 5, 12, 20}, |)
全序排列:1 ≺ 5 ≺ 2 ≺ 4 ≺ 20 ≺ 12(这里先删除5和先删除2是一样的)
拓扑排序下面的哈塞图