【刷题笔记】更骚的并查集

更骚的并查集

写在前面

打个小广告：

最近在学Golang，开了用Go语言实现算法的仓库，有兴趣的同学们可以来贡献哦～

网址在这⬇️

Project alGo

如果你每天有力扣每日一题的习惯，你可能会感叹：

1月可真是一个图论月

确实如此，

而并查集是解决连通分量问题以及具有传递关系问题的特色解法

并查集

并查集本身有两个优化方案：

• 路径压缩
  • 在 Find() 方法中，将子树的节点拉到根节点，如此提高查找效率。
• 按秩合并
  • 维护每个节点子树的高度或节点数量，在合并时考察这个值。

我们要清楚并查集的作用是：

将两个联通分量合并成一个联通分量。

803. 打砖块

问题描述

有一个 m x n 的二元网格，其中 1 表示砖块，0 表示空白。砖块 稳定（不会掉落）的前提是：

一块砖直接连接到网格的顶部，或者
至少有一块相邻（4 个方向之一）砖块 稳定 不会掉落时
给你一个数组 hits ，这是需要依次消除砖块的位置。每当消除 hits[i] = (rowi, coli) 位置上的砖块时，对应位置的砖块（若存在）会消失，然后其他的砖块可能因为这一消除操作而掉落。一旦砖块掉落，它会立即从网格中消失（即，它不会落在其他稳定的砖块上）。

返回一个数组 result ，其中 result[i] 表示第 i 次消除操作对应掉落的砖块数目。

注意，消除可能指向是没有砖块的空白位置，如果发生这种情况，则没有砖块掉落。

示例 1：

输入：grid = [[1,0,0,0],[1,1,1,0]], hits = [[1,0]]
输出：[2]
解释：
网格开始为：
[[1,0,0,0]，
 [1,1,1,0]]
消除 (1,0) 处加粗的砖块，得到网格：
[[1,0,0,0]
 [0,1,1,0]]
两个加粗的砖不再稳定，因为它们不再与顶部相连，也不再与另一个稳定的砖相邻，因此它们将掉落。得到网格：
[[1,0,0,0],
 [0,0,0,0]]
因此，结果为 [2] 

示例 2：

输入：grid = [[1,0,0,0],[1,1,0,0]], hits = [[1,1],[1,0]]
输出：[0,0]
解释：
网格开始为：
[[1,0,0,0],
 [1,1,0,0]]
消除 (1,1) 处加粗的砖块，得到网格：
[[1,0,0,0],
 [1,0,0,0]]
剩下的砖都很稳定，所以不会掉落。网格保持不变：
[[1,0,0,0], 
 [1,0,0,0]]
接下来消除 (1,0) 处加粗的砖块，得到网格：
[[1,0,0,0],
 [0,0,0,0]]
剩下的砖块仍然是稳定的，所以不会有砖块掉落。
因此，结果为 [0,0] 。

思路

我们知道，并查集的思想，

是将两个分立的节点集合组成一个连通分量

我们观察这道题的题意：

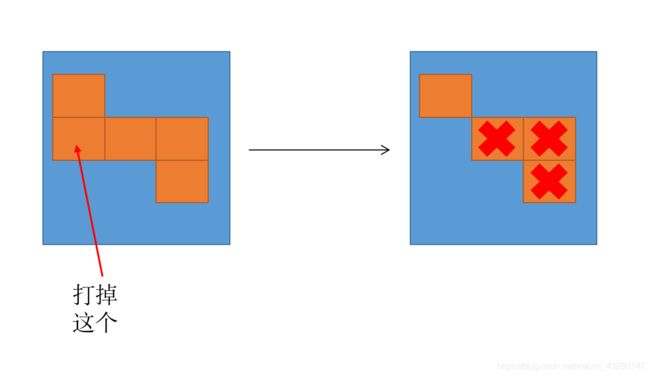
每当消除 hits[i] = (rowi, coli) 位置上的砖块时，
对应位置的砖块（若存在）会消失，
然后其他的砖块可能因为这一消除操作而掉落。

我来翻译一下这句话：

当一个连通分量的根节点被打掉之后，

该连通分量的其他节点会相应被消失

想了20分钟，这似乎并不能用并查集来解决

因为并查集解决的是将两个集合分量Union（连通）在一起

而这里的过程是将两个分量拆开

当然不能，但是如果倒着来一遍呢？就像TENET 的剧情那样

这一切都顺理成章了，两个分开的元素被原来打掉的元素合并在了一起。

这便是这道题的关键思想。

编码

1. 首先，既然用到了并查集，我们应该把并查集的代码模版先写出来，读者可以试着自己默写一遍，回过头来看这段代码：

	// 并查集的底层 size稍后解释
	parent := make([]int,size+1)
	// 并查集每个元素的秩，即根节点对应的集合大小
	ufsize := make([]int,size+1)

	// initiating
	// -----------------------------------
	for i := 0;i<=size;i++ {
		parent[i] = i
		ufsize[i] = 1
	}

	var Find = func(x int) int {
		root := x
		for root != parent[root] {
			root = parent[root]
		}
		// 路径压缩
		parent[x] = root
		return root

	}

	var Union = func(x, y int) {
		rootX, rootY := Find(x), Find(y)
		if rootX == rootY {
			return
		}
    // 按秩合并（小集合合并入大集合），提高平衡度
		if ufsize[rootX] < ufsize[rootY] {
			parent[rootX] = rootY
			ufsize[rootY] += ufsize[rootX]
		} else {
			parent[rootY] = rootX
			ufsize[rootX] += ufsize[rootY]
		}
		return
	}

2. 我们知道，并查集的底层需要存储问题空间里每一个元素（这里是指网格中的砖块）。那么如何用一维的数组存储一个二维空间的全体元素？

   这个问题也相当简单：

   // cols代表grid的总列数
   x * cols + y 
   

   二维的网格被压扁成了一个一维数组，下标则被表示成了一行

   可以得到，这个一位数组（并查集底层）的大小为

   // rows为总行数 cols为总列数
   size = rows * cols 
   

3. 如何求得连带掉落的砖块个数？

   我们知道，从反向思维的角度，

   即从砖块被打碎的状态到完整的状态，这里打碎的状态不用囊括附带掉落的砖块，因为题目只是要求返回其个数。

   个数即一个集合中打碎前后元素的个数之差：

   res = size_origin - size_current -1  // -1是因为不包括打碎的那个砖块
   

解决了如上的问题后，编码将会相对轻松，我将分模块讲解编码思路：

1. 我们需要从打碎后的网格状态，因此需要深拷贝一个数组

插一句，由于go语言的Slice类型是引用类型，我们这里需要用到深拷贝，即自己手动拷贝数组的每一个元素，或者调用Go语言提供的built-in API:

func copy(dst, src[]Type)

​ 我们将拷贝的数组初始化到打碎后到样子：

	for _,hit := range hits {
		copyArr[hit[0]][hit[1]] = 0
	}

2. 接下来就是构造打碎后的并查集了：

这里有一个小trick: 就是将并查集的最后一个元素作为根节点，这个根节点不保存任何信息，这一点请在初始化parent数组时多加注意⚠️

// step1. 根据题意构造根节点与屋顶（第一行）砖块的集合关系
	for j:=0;j< cols ;j++ {
		if copyArr[0][j] == 1 {
			Union(j,size)
		}
	}

	// step2. 构造剩下砖块的并查关系
	for i:=1;i<rows;i++ {
		for j:=0;j<cols;j++ {
			if copyArr[i][j] == 1 {
				if copyArr[i-1][j] == 1 {
					Union(getIndex(i-1,j),getIndex(i,j))
				}
				if j>0 && copyArr[i][j-1] == 1 {
					Union(getIndex(i,j-1),getIndex(i,j))
				}
			}
		}
	}

3. 接下来就是把被打碎的砖块**“补”**回去了

   我们只需要倒着遍历输入进来的 hits 数组，

   然后得到每一步操作前后的集合秩之差，

   即可得到每次操作的结果

   // step3. 遍历整个打碎后的网格
   // 把砖块一步步填回去
   for i:= hitsLen-1;i>=0;i-- {
      // 得到当前这个被打碎砖块的坐标
      x := hits[i][0]
      y := hits[i][1]
      // 本来没有砖块，我们跳过这个网格
      if grid[x][y] == 0 {
         continue
      }
   
      // 得到当前这个集合打碎前后的秩
      origin := getSize(size)
   
   
      // 如果是屋顶的砖块
      if x==0 {
         Union(y, size)
      }
      var (
         MVX = [4]int{0,1,0,-1}
         MVY = [4]int{1,0,-1,0}
      )
   
      for k:=0;k<4;k++ {
         newX := x + MVX[k]
         newY := y + MVY[k]
   			
         if inArea(newX,newY)&& copyArr[newX][newY] == 1 {
            Union(getIndex(x,y),getIndex(newX,newY))
         }
      }
   
      // 得到当前这个集合打碎前的秩
      current := getSize(size)
   
      if current - origin-1 < 0 {
         res[i] =0
      } else {
         res[i] = current - origin -1
      }
      // 补上这个砖块
      copyArr[x][y] = 1
      }
   

分析

• 这道题告诉我们，当正向思维无法解决问题时，可以尝试逆向思维。
• 分析复杂度：
  • 时间复杂度： $O(length(hits)+cols\times rows)$
  • 空间复杂度：$O(cols\times rows)$

完整代码

完整的代码已经上传到仓库上，如果你有更加neaty的实现，欢迎贡献哦～

源码地址

REF

https://leetcode-cn.com/problems/bricks-falling-when-hit/solution/803-da-zhuan-kuai-by-leetcode-r5kf/

https://en.wikipedia.org/wiki/Disjoint-set_data_structure