【算法实验】算法分析与设计第三次实验Lab3

第1关：加1乘2平方

描述
最简单的队列的使用
#include
#include
using namespace std;

queue q1;
int main()
{
int temp, x;
q1.push(5);//入队
q1.push(8);//入队
temp = q1.front();//访问队首元素
q1.pop();//出队
q1.empty();//判队列是否为空
q1.back();//返回队尾元素
q1.size();//返回队列长度
}

给定两个正整数m、n，问只能做加1、乘2和平方这三种变化，从m变化到n最少需要几次

输入
输入两个10000以内的正整数m和n，且m小于n

输出
输出从m变化到n的最少次数

输入样例
1 16

输出样例
3

#include 
#include 
using namespace std;

queue<int> q;
int m, n;
int step[10000], used[10000];

/**
 * 判断是否到达结果的函数
 * 如果没有被用过，used赋1，步数加一
 * 如果next == n，返回true，否则入队
*/
bool judge(int now, int next)
{
    if(next <= n && !used[next])
    {
        used[next] = 1;
        step[next] = step[now] + 1;
        if(next == n)
            return true;
        else
            q.push(next);
    }
    return false;
}

/**
 * 进行加一乘二平方三项操作的函数
*/
int change(int now, int i)
{
    if(i == 0)
        return now + 1;
    else if(i == 1)
        return now * 2;
    else
        return now * now;
}

/**
 * 分支限界法-广搜
 * 
 * 判断队列是否为空
 * 如果不为空，当前数字为队头元素，进行广搜
*/
int bfs()
{
    while(!q.empty())
    {
        int now = q.front();
        q.pop();
        used[now] = 1;
        for(int i = 0; i < 3; i++)
        {
            int next = change(now, i);
            if(judge(now, next))
                return step[next];
        }
    }
    return 0;
}

int main()
{
    cin >> m >> n;
    q.push(m);
    cout << bfs() << endl;
    return 0;
}

第2关：电子老鼠闯迷宫

描述
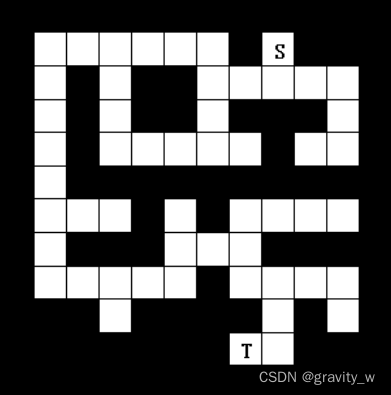
有一只电子老鼠被困在如下图所示的迷宫中。这是一个12*12单元的正方形迷宫，黑色部分表示建筑物，白色部分是路。电子老鼠可以在路上向上、下、左、右行走，每一步走一个格子。现给定一个起点S和一个终点T，求出电子老鼠最少要几步从起点走到终点。

输入
本题包含一个测例。在测例的第一行有四个由空格分隔的整数，分别表示起点的坐标S（x.y）和终点的坐标T（x,y）。从第二行开始的12行中，每行有12个字符，描述迷宫的情况，其中’X’表示建筑物，'.'表示路.

输出
输出一个整数，即电子老鼠走出迷宫至少需要的步数。

输入样例
2 9 11 8
XXXXXXXXXXXX
X…X.XXX
X.X.XX…X
X.X.XX.XXX.X
X.X…X…X
X.XXXXXXXXXX
X…X.X…X
X.XXX…XXXX
X…X…X
XXX.XXXX.X.X
XXXXXXX…XXX
XXXXXXXXXXXX

输出样例
28

#include 
#include 
using namespace std;

int bx, by, ex, ey;
char maze[12][12];
int step[12][12], used[12][12];
int nextstep[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};    //上左右下
queue<int> q;

int newplace(int x, int y, int i)
{
    int x2 = x + nextstep[i][0];
    int y2 = y + nextstep[i][1];
    if(x2 >= 0 && x2 < 12 && y2 >= 0 && y2 < 12 && used[x2][y2] == 0 && maze[x2][y2] == '.')
    {
        used[x2][y2] = 1;
        step[x2][y2] = step[x][y] + 1;
        q.push(x2 * 12 + y2);
        return x2 * 12 + y2;
    }
    else
        return -1;
}

void bfs()
{
    while(!q.empty())
    {
        int now = q.front();
        q.pop();
        int x1 = now / 12;
        int y1 = now % 12;
        for(int i = 0; i < 4; i++)
        {
            int next = newplace(x1, y1, i);
            if(next != -1)
            {
                int x2 = next / 12;
                int y2 = next % 12;
                if(x2 == ex && y2 == ey)
                    return;
            }
        }
    }
}

int main()
{
    cin >> bx >> by >> ex>> ey;
    for(int i = 0; i < 12; i++)
    {
        cin >> maze[i];
    }
    q.push((bx - 1) * 12 + (by - 1));
    bfs();
    cout << step[ex - 1][ey - 1] << endl;
    return 0;
}

第3关：跳马

描述
在国际象棋中，马的走法与中车象棋类似，即俗话说的“马走日”，下图所示即国际象棋中马（K）在一步能到达的格子（其中黑色的格子是能到达的位置）。

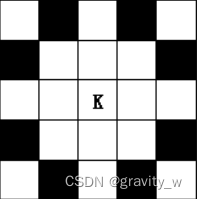
现有一200*200大小的国际象棋棋盘，棋盘中仅有一个马，给定马的当前位置（S）和目标位置（T），求出马最少需要多少跳才能从当前位置到达目标位置。

输入
本题包含多个测例。输入数据的第一行有一个整数N（1<=N<=1000），表示测例的个数，接下来的每一行有四个以空格分隔的整数，分别表示马当前位置及目标位置的横、纵坐标C（x,y）和G（x,y）。坐标由1开始。

输出
对于每个测例，在单独的一行内输出一个整数，即马从当前位置跳到目标位置最少的跳数。

输入样例
2
1 1 2 1
1 5 5 1

输出样例
3
4

#include 
#include 
using namespace std;

int n;
int bx, by, ex, ey;
int step[200][200], used[200][200];
int nextplace[8][2] = {-1, -2,  -2, -1,  -2, 1,  -1, 2,  1, -2,  2, -1,  2, 1,  1, 2};
queue<int> q;

int newplace(int x, int y, int i)
{
    int x2 = x + nextplace[i][0];
    int y2 = y + nextplace[i][1];
    if(x2 >= 0 && x2 < 200 && y2 >= 0 && y2 < 200 && used[x2][y2] == 0)
    {
        used[x2][y2] = 1;
        step[x2][y2] = step[x][y] + 1;
        q.push(x2 * 200 + y2);
        return x2 * 200 + y2;
    }
    else
        return -1;
}

void bfs()
{
    while(!q.empty())
    {
        int now = q.front();
        q.pop();
        int x1 = now / 200;
        int y1 = now % 200;
        for(int i = 0; i < 8; i++)
        {
            int next = newplace(x1, y1, i);
            if(next != -1)
            {
                int x2 = next / 200;
                int y2 = next % 200;
                if(x2 == (ex - 1) && y2 == (ey - 1))
                    return;
            }
        }
    }
}

int main()
{
    cin >> n;
    while(n--)
    {
        cin >> bx >> by >> ex >> ey;
        q.push((bx - 1) * 200 + by - 1);
        used[bx - 1][by - 1] = 1;
        bfs();
        cout << step[ex - 1][ey - 1] << endl;
        for(int i = 0; i < 200; i++)
        {
            for(int j = 0; j < 200; j++)
            {
                used[i][j] = 0, step[i][j] = 0;
            }
        }
        while(!q.empty())
            q.pop();
    }
    return 0;
}

第4关：独轮车

描述
独轮车的轮子上有红、黄、蓝、白、绿（依顺时针序）5种颜色，在一个如下图所示的20*20的迷宫内每走一个格子，轮子上的颜色变化一次。独轮车只能向前推或在原地转向。每走一格或原地转向90度均消耗一个单位时间。现给定一个起点（S）和一个终点（T），求独轮车以轮子上的指定颜色到达终点所需的最短时间。

输入
本题包含一个测例。测例中分别用一个大写字母表示方向和轮子的颜色，其对应关系为：E-东、S-南、W-西、N-北；R-红、Y-黄、B-蓝、W-白、G-绿。在测试数据的第一行有以空格分隔的两个整数和两个大写字母，分别表示起点的坐标S（x,y）、轮子的颜色和开始的方向，第二行有以空格分隔的两个整数和一个大写字母，表示终点的坐标T（x,y）和到达终点时轮子的颜色，从第三行开始的20行每行内包含20个字符，表示迷宫的状态。其中’X’表示建筑物，'.'表示路.

输出
在单独的一行内输出一个整数，即满足题目要求的最短时间。

输入样例
3 4 R N
15 17 Y
XXXXXXXXXXXXXXXXXXXX
X.X…XXXXXX…XX
X.X.X…X…XXXX…X
X.XXXXXXX.XXXXXXXX.X
X.X.XX…X…X
X…XXXXX.X.XX.X.XXX
X.X.XX…X.X…X.X.X
X.X.X…XX…XXXX.XXX
X.X.XX.XX.X…X.X.X
X.X…XX.X.XX.X.X.X
X.X.X.XXXXX.XX.X.XXX
X.X.X.XXXXX…X…X
X.X…X.XX…X.X
X.XXX.XXX.X.XXXXXXXX
X…XX…X…X
XXXXX…X.XXXXXXX.X
X…XXXXXXX.XXX.XXX.X
X.XX…X…X
X…X.XXXX.XXXX…XXX
XXXXXXXXXXXXXXXXXXXX

输出样例
56

提示
56

#include 
#include 
using namespace std;

int n;
int bx, by, ex, ey, b_c, b_l, e_c;
char bc, bl, ec;
char maze[21][21];
int step[21][21][5][4], used[21][21][5][4];
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};

typedef struct node
{
    int color;
    int location;
    int x, y;
} node;

queue<node> q;

node newplace(node n, int i)
{
    if(i == 0)
    {
        n.color = (n.color + 1) % 5;
        n.x = n.x + dx[n.location];
        n.y = n.y + dy[n.location];
    }
    else if(i == 1)
    {
        n.location = (n.location + 1) % 4;
    }
    else
    {
        n.location=(n.location + 3) % 4;
    }
    return n;
}

int bfs()
{
    node n1, n2;
    n1.x = bx;
    n1.y = by;
    n1.color = b_c;
    n1.location = b_l;
    q.push(n1);
    while(!q.empty())
    {
        n1 = q.front();
        q.pop();
        for(int i = 0; i < 3; i++)
        {
            n2 = newplace(n1, i);
            if(n2.x == ex && n2.y == ey && n2.color == e_c)
                return step[n1.x][n1.y][n1.color][n1.location] + 1;
            if(n2.x > 0 && n2.y < 21 && n2.y > 0 && n2.y < 21 && used[n2.x][n2.y][n2.color][n2.location] == 0 && maze[n2.x][n2.y] == '.')
            {
                q.push(n2);
                used[n2.x][n2.y][n2.color][n2.location] = 1;
                step[n2.x][n2.y][n2.color][n2.location] = step[n1.x][n1.y][n1.color][n1.location] + 1;
            }
        }
    }
    return -1;
}

int changecolor(char c)
{
    if(c == 'R')
        return 0;
    else if(c == 'Y')
        return 1;
    else if(c == 'B')
        return 2;
    else if(c == 'W')
        return 3;
    else 
        return 4;
}

int changedir(char d)
{
    if(d == 'E')
        return 0;
    else if(d == 'S')
        return 1;
    else if(d == 'W')
        return 2;
    else
        return 3;
}

int main()
{
    cin >> bx >> by >> bc >> bl;
    cin >> ex >> ey >> ec;

    b_c = changecolor(bc);
    b_l = changedir(bl);
    e_c = changecolor(ec);

    for(int i = 1; i < 21; i++)
    {
        for(int j = 1; j < 21; j++)
            cin >> maze[i][j];
    }

    used[bx][by][b_c][b_l] = 1;
    int result = bfs();
    cout << result << endl;

    return 0;
}

第5关：六数码问题

描述
现有一两行三列的表格如下：

A B C
D E F

把1、2、3、4、5、6六个数字分别填入A、B、C、D、E、F格子中，每个格子一个数字且各不相同。每种不同的填法称为一种布局。如下：

1 3 5
2 4 6
布局1

2 5 6
4 3 1
布局2

定义α变换如下：把A格中的数字放入B格，把B格中的数字放入E格，把E格中的数字放入D格，把D格中的数字放入A格。
定义β变换如下：把B格中的数字放入C格，把C格中的数字放入F格，把F格中的数字放入E格，把E格中的数字放入B格。

问：对于给定的布局，可否通过有限次的α变换和β变换变成下面的目标布局：

1 2 3
4 5 6
目标布局

输入
本题有多个测例，每行一个，以EOF为输入结束标志。每个测例的输入是1到6这六个数字的一个排列，空格隔开，表示初始布局ABCDEF格中依次填入的数字。

输出
每个输出占一行。可以转换的，打印Yes；不可以转换的，打印No。

输入样例
1 3 5 2 4 6
2 5 6 4 3 1

输出样例
No
Yes

提示
第二个示例即布局2的一种转换方法：αααβαα

#include
#include
using namespace std;

typedef struct node
{
	int table[6];
	int num;
} node;

node start;
queue<node> q;
int used[654322];

int setnum(node n)
{
	n.num = 0;
	for(int i = 0; i < 6; i++)
	{
		n.num *= 10;
		n.num += n.table[i];
	}
	return n.num;
}

bool istarget(node n)
{
	if(n.num == 123456) 
        return true;
	else 
        return false;
}

node operate(node now,int i)
{
	node next;
	if(i == 0)
	{
		next.table[0] = now.table[3];
		next.table[1] = now.table[0];
		next.table[2] = now.table[2];
		next.table[3] = now.table[4];
		next.table[4] = now.table[1];
		next.table[5] = now.table[5];
	}
	if(i==1)
	{
	    next.table[0] = now.table[0];
		next.table[1] = now.table[4];
		next.table[2] = now.table[1];
		next.table[3] = now.table[3];
		next.table[4] = now.table[5];
		next.table[5] = now.table[2];	
	}
	next.num = setnum(next);
	return next;
}

void init()
{
	for(int i = 123456; i < 654322; i++)
	{
		used[i] = 0;
	}
	while(!q.empty())
	{
		q.pop();
	}
	q.push(start);
	used[start.num] = 1;
}

bool bfs()
{
	node now, next;
	while(!q.empty())
	{
		now = q.front();
		q.pop();
		for(int i = 0; i < 2; i++)
		{
			next = operate(now,i);
			if(!used[next.num])
			{
				used[next.num]=1;
				if(istarget(next)) 
                    return true;
				else 
                    q.push(next);
			}
		}
	}
	return false;
}

int main()
{
	while(cin >> (start.table[0]))
	{
		for(int i = 1; i < 6; i++)
		{
			cin >> start.table[i];
		}
		start.num = setnum(start);
		init();
		if(bfs()) 
            cout<<"Yes"<<endl;
		else 
            cout<<"No"<<endl;
	}
	return 0;
}

第6关：木乃伊迷宫

描述
木乃伊地下宫殿是一个6行6列的迷宫。作为敢到木乃伊地下宫殿里去探险的你，有没有跟木乃伊抓迷藏的心理准备呵！游戏在木乃伊所在的迷宫里展开，任务就是尽快赶到出口。你一次只能走一步，而木乃伊可以走两步，但木乃伊是很笨的，他总是先尽量跟你达到同一列，如果已经是同一列了，他才会像你走来，有墙的地方人和木乃伊都不能过，你可以利用障碍物牵制住木乃伊。

输入
先输入墙的数量n，然后在后续的n行里每行有3个数表示一堵墙，3个数分别为格子的行、列和墙的位置（0表示这个格子的下方是墙，1表示这个格子的右方是墙），再下来的3行每行2个数，分别表示木乃伊、人还有出口的位置。

输出
如果能安全逃生则输出Yes,否则输出No,答案占一行。

输入样例
5
0 0 0
1 1 1
1 4 1
3 4 1
4 3 0
3 3
3 1
5 5

输出样例
No

#include 
#include 
using namespace std;

struct node
{
    int mx, my;
    int px, py;
    bool useful;
};
node start, exit_;
int n, x, y, l;
int maze[6][6][2];
int used[6][6][6][6];
int nextstep[4][2] = {0, -1, 1, 0, 0, 1, -1, 0}; //左下右上
queue<node> q;

/**
 * 判断是否是墙的函数
 * 
 * 如果是墙返回1，否则返回0
*/
bool iswall(int x, int y, int i)
{
    switch(i)
    {
		case 0:
			return maze[x][y - 1][1];
		case 1:
			return maze[x][y][0];
		case 2:
			return maze[x][y][1];
		case 3:
			return maze[x - 1][y][0];
        default:
            return false;
    }
}

/**
 * 判断下一个节点是否有效
 * 
 * 如果人走的下一个节点不满足条件，返回false
 * 两次循环僵尸，先同列再同行（注意next和now，注意m和n，注意x和y啊啊啊啊啊啊啊啊啊不然调好久不知道是哪里的问题）
 * 判断僵尸是否追上
 * 判断节点是否使用过
*/
node nextplace(node now, int i)
{
    node next;
    next.px = now.px + nextstep[i][0], next.py = now.py + nextstep[i][1];
    if(next.px < 0 || next.px > 5 || next.py < 0 || next.py > 5 || iswall(now.px, now.py, i))
    {
        next.useful = false;
        return next;
    }
    else
    {
        next.mx = now.mx, next.my = now.my;
        for(int m = 0; m < 2; m++)
        {
            if((next.my < next.py) && !iswall(next.mx, next.my, 2))
                next.my++;
            else if((next.my > next.py) && !iswall(next.mx, next.my, 0))
                next.my--;
            else if(next.my == next.py)
            {
                if((next.mx < next.px) && !iswall(next.mx, next.my, 1))
                    next.mx++;
                else if((next.mx > next.px) && !iswall(next.mx, next.my, 3))
                    next.mx--;
                else if(next.mx == next.px)
                {
                    next.useful = false;
                    return next;
                }
            }
        }
    }
    if(next.mx == next.py && next.my == next.py)
    {
        next.useful = false;
        return next;
    }

    if(used[next.mx][next.my][next.px][next.py])
        next.useful = false;
    else
    {
        used[next.mx][next.my][next.px][next.py] = 1;
        next.useful = true;
    }
    return next;
}

int bfs()
{
    while(!q.empty())
    {
        node now = q.front();
        q.pop();
        for(int i = 0; i < 4; i++)
        {
            node next = nextplace(now, i);
            if(next.useful)
            {
                if(next.px == exit_.px && next.py == exit_.py)
                    return 1;
                q.push(next);
            }
        }
    }
    return 0;
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> x >> y >> l;
        maze[x][y][l] = 1;
    }
    cin >> start.mx >> start.my >> start.px >> start.py >> exit_.px >> exit_.py;
    used[start.mx][start.my][start.px][start.py] = 1;
    q.push(start);
    if(bfs())
        cout << "Yes" << endl;
    else
        cout << "No" << endl;
    return 0;
}

第7关：推箱子

描述
绝大多数人都玩过推箱子的游戏，控制一个人将箱子推动到目标位置即获得胜利。现请你编写一个程序，判断将箱子推到目标位置至少需要多少步。

输入
推箱子的平面区域为固定大小（10*10），使用10行10列输入推箱子的初始局面。其中，0代表空格，1代表墙，2代表箱子，3代表目标位置，4代表人。
注：游戏中只有一个箱子，一个目标位置，一个人。

输出
输出将箱子推到目标位置的最小步数；若箱子不可能被推到目标位置，输出-1。

输入样例
0000000000
0000000300
0100000000
0100000000
0101111100
0000010000
0000010000
0020010040
0000010000
0000010000

输出样例
34

#include 
#include 
using namespace std;

struct node
{
    int bx, by;
    int px, py;
    bool useful;
};
node start, end_;
queue<node> q;
char maze[10][10];
int used[10][10][10][10], step[10][10][10][10];
int nextstep[4][2] = {0, -1,  1, 0,  0, 1,  -1, 0}; //左下右上

/**
 * 判断下个节点的函数
 * 
 * 如果不符合条件（如x、y不在范围内，下个节点是墙），直接false并返回
 * 如果符合条件，判断人与箱子的位置是否重叠，如果重叠判断箱子是否可以向前推（注意同样判断xy范围和墙），不能推false并返回
 * 满足条件且没有使用过的节点，used置1，step+1，置true并返回
*/
node newplace(int i, node now)
{
    node next;
    next.px = now.px + nextstep[i][0], next.py = now.py + nextstep[i][1];
    next.bx = now.bx, next.by = now.by;
    if(next.px < 0 || next.px >= 10 || next.py < 0 || next.py >= 10 || maze[next.px][next.py] == '1')
    {
        next.useful = false;
        return next;
    }
    if(next.px == next.bx && next.py == next.by)
    {
        next.bx = next.bx + nextstep[i][0], next.by = next.by + nextstep[i][1];
        if(next.bx < 0 || next.bx >= 10 || next.by < 0 || next.by >= 10 || maze[next.bx][next.by] == '1')
        {
            next.useful = false;
            return next;
        }
    }
    if(used[next.bx][next.by][next.px][next.py] == 1)
    {
        next.useful = false;
        return next;
    }
    used[next.bx][next.by][next.px][next.py] = 1;
    step[next.bx][next.by][next.px][next.py] = step[now.bx][now.by][now.px][now.py] + 1;
    next.useful = true;
    return next;
}

int bfs()
{
    while(!q.empty())
    {
        node now = q.front();
        q.pop();
        for(int i = 0; i < 4; i++)
        {
            node next = newplace(i, now);
            if(next.useful)
            {
                if(next.bx == end_.bx && next.by == end_.by)
                    return step[next.bx][next.by][next.px][next.py];
                q.push(next);
            }
        }
    }
    return -1;
}

int main()
{
    for(int i = 0; i < 10; i++)
    {
        for(int j = 0; j < 10; j++)
        {
            cin >> maze[i][j];
            if(maze[i][j] == '2')
                start.bx = i, start.by = j;
            if(maze[i][j] == '4')
                start.px = i, start.py = j;
            if(maze[i][j] == '3')
                end_.bx = i, end_.by = j;
        }
    }
    maze[start.bx][start.by] = maze[start.px][start.py] = maze[end_.bx][end_.by] = '0';
    q.push(start);
    used[start.bx][start.by][start.px][start.py] = 1;
    cout << bfs() << endl;
    return 0;
}

第8关：polygon

描述
在一个周长为10000的圆上等距分布着n个点，即这n个点是一个正n边形的顶点。现在要另加m个点到圆上，新加的m个点可以任意选择位置（可以与原有的点重合）。然后将这n+m个点中的一些点延圆周移动，最终使n+m个点均匀分布，即在一个正n+m边形的顶点上。输出最小总移动距离。

输入
输入两个整数 n, m。 (2≤n≤1000, 1≤m≤1000).

输出
输出最小总移动距离，保留4位小数。

输入样例
sample input #1 2 1 sample input #2 2 3 sample input #3 3 1 sample input #4 10 10

输出样例
sample output #1 1666.6667 sample output #2 1000.0 sample output #3 1666.6667 sample output #4 0.0 图对应前3个样例

#include 
#include 
#include 
using namespace std;

/**
 * 假设总距离为n + m，每个点的位置为1,2,3……（整数）
 * 
 * n的距离是固定的，即平分放置
 * 而要使移动距离最小，则假设m个点直接放置在不需要移动的位置
 * 
 * 首先计算出每个n的初始位置，然后初始位置+0.5计算出每个n距离最近的整数，相减并累加起来就是需要移动的距离
 * 最后将距离根据弧长换算成真正的距离
*/
int main()
{
	int n, m;
	double pos, dis;   
 
	while(cin >> n >> m)
	{
		dis = 0;	
		for(int i = 0; i < n; i++)	
		{
			pos = (double)i / n * (n+m);	    
			dis += fabs((int)(pos + 0.5) - pos);	
		}
		dis = (double)dis / (m+n) * 10000;	
        cout.setf(ios::fixed);
        cout << setprecision(4) << dis << endl;
	}
	return 0;
}

第9关：八数码

描述
在九宫格里放在1到8共8个数字还有一个是空格，与空格相邻的数字可以移动到空格的位置，问给定的状态最少需要几步能到达目标状态（用0表示空格）：
1 2 3
4 5 6
7 8 0

输入
输入一个给定的状态。

输出
输出到达目标状态的最小步数。不能到达时输出-1。

输入样例
1 2 3
4 0 6
7 5 8

输出样例
2

#include 
#include 
#include 
using namespace std;

int code[3][3];
int nextcode[4][2] = {0, -1,  -1, 0,  0, 1,  1, 0};
queue<int> q;
map<int, int> used, step;

int trans(int code[3][3])
{
    int num = 0;
    for(int i = 0; i < 3; i++)
    {
        for(int j = 0; j < 3; j++)
            num = (num * 10) + code[i][j];
    }
    return num;
}

int newnum(int temp[3][3], int m, int n, int num, int i)
{
    int x = m + nextcode[i][0], y = n + nextcode[i][1];
    if(x >= 0 && x <= 2 && y >= 0 && y <= 2)
    {
        int swap = temp[x][y];
        temp[x][y] = temp[m][n];
        temp[m][n] = swap;
        int num2 = trans(temp);
        if(used.count(num2) == 0)
        {
            q.push(num2);
            used[num2] = 1;
            step[num2] = step[num] + 1;
            temp[m][n] = temp[x][y];
            temp[x][y] = swap;
            return num2;
        }
        else
        {
            temp[m][n] = temp[x][y];
            temp[x][y] = swap;
            return -1;
        }
    }
    else 
        return -1;
}

int bfs()
{
    while(!q.empty())
    {
        int num = q.front();
        int use = num;
        q.pop();
        int temp[3][3];
        int m, n;
        for(int i = 2; i >= 0; i--)
        {
            for(int j = 2; j >= 0; j--)
            {
                temp[i][j] = use % 10, use /= 10;
                if(temp[i][j] == 0)
                {
                    m = i, n = j;
                }
            }
        }
        for(int i = 0; i < 4; i++)
        {
            int re = newnum(temp, m, n, num, i);
            if(re != -1)
            {
                if(re == 123456780)
                    return step[re];
            }
        }
    }
    return -1;
}

int main()
{
    for(int i = 0; i < 3; i++)
    {
        for(int j = 0; j < 3; j++)
            cin >> code[i][j];
    }
    int num = trans(code);
    q.push(num);
    used[num] = 1, step[num] = 0;
    int result = bfs();
    cout << result << endl;
    return 0;
}

第10关：僵尸来了

描述
僵尸要来佳佳家做客了，佳佳把花园布置了一下，你拿到了花园的地图（以二维矩阵的形式表示）以及起点和佳佳家的位置。花园里某些位置有地刺，僵尸过的时候每次需要消耗一个单位的生命值，僵尸有一定数量的生命值，看看最聪明的僵尸能否在天亮前到达你的家里？能的话，最少花费多少时间。

输入
输入的第一行包含三个整数：m，n，t。代表m行n列的地图和僵尸的生命值t。m,n都是小于200的正整数，t是小于10的正整数，第2行开始的m行是m行n列的花园地图，其中!代表起点，+表示佳佳家。*代表通路，w代表地刺。

输出
输出僵尸到达佳佳家最少需要花费的时间。如果无法到达，则输出-1。

输入样例
4 4 2
w!ww
**ww
www+

输出样例
6

//结构体才是最终归宿，不要挣扎了啊！！！
#include 
#include 
using namespace std;

struct zombie
{
    int t;
    int step;
    int x, y;
    bool judge;
};

int m, n, t;    //m行n列地图，僵尸生命为t
char maze[200][200];
int used[200][200][10];    //注意used是三维，因为血量也是一维数据
int nextstep[4][2] = {0, -1,  -1, 0,  0, 1,  1, 0};
queue<zombie> q;
zombie begin_, end_;

zombie newplace(int i, zombie now)
{
    zombie next;
    next.x = now.x + nextstep[i][0];
    next.y = now.y + nextstep[i][1];
    if(next.x >= 0 && next.y >= 0 && next.x < m && next.y < n)
    {
        if(maze[next.x][next.y] == 'w')
            next.t = now.t - 1;
        else
            next.t = now.t;

        if(next.t <= 0 || used[next.x][next.y][next.t] == 1)
        {
            next.judge = false;
            return next;
        }
    }
    else
    {
        next.judge = false;
        return next;
    }
    used[next.x][next.y][next.t] = 1;
    next.step = now.step + 1;
    q.push(next);
    return next;
}

int bfs()
{
    while(!q.empty())
    {
        zombie now = q.front();
        q.pop();
        if(now.x == end_.x && now.y == end_.y)
        {
            return now.step;
        }
        for(int i = 0; i < 4; i++)
        {
            zombie next = newplace(i, now);
        }
    }
    return -1;
}

int main()
{
    cin >> m >> n >> t;
    for(int i = 0; i < m; i++)
    {
        for(int j = 0; j < n; j++)
        {
            cin >> maze[i][j];
            if(maze[i][j] == '!')
                begin_.x = i, begin_.y = j;
            if(maze[i][j] == '+')
                end_.x = i, end_.y = j;
        }
    }

    begin_.t = t, begin_.step = 0;
    used[begin_.x][begin_.y][begin_.t] = 1;
    q.push(begin_);
    cout << bfs();

    return 0;
}

第11关：僵尸又来了

描述
由于聪明的佳佳很善于布置花园，所以僵尸没能在天亮之前冲到佳佳家里，这次僵尸又要来佳佳家做客了，佳佳很高兴，因为姑妈送给佳佳的大嘴花派上了用场。你拿到了花园的地图（以二维矩阵的形式表示）以及起点和佳佳家的位置。花园里一个位置有大嘴花，僵尸到达时会被吃掉，同时从起点又会出来一个新的僵尸，如果僵尸到达大嘴花的位置时，前一个僵尸还没有吃完，大嘴花将被吃掉，看看僵尸能否在天亮前到达佳佳家里？能的话，最少花费多少时间。

输入
输入的第一行包含4个整数：m，n，t, p。代表m行n列的地图、大嘴花吃掉僵尸花费的时间t和距离天亮的时间p。m,n都是小于200的正整数，t是小于10的正整数，第2行开始的m行是m行n列的花园地图，其中!代表起点，+表示佳佳家。*代表通路，@代表大嘴花，#表示墙。

输出
输出僵尸到达佳佳家最少需要花费的时间。如果在天亮之前无法到达，则输出-1。

输入样例
4 4 5 50
#!##
**##
**#+
***@

输出样例
-1

#include
#include
using namespace std;

struct node
{
    int x, y;
    int alltime, ftime;
    bool useful;
};

int m, n, t, p;
char maze[100][100];
int used[100][100][20];
int nextstep[4][2] = {-1, 0,  0, 1,  1, 0,  0, -1};
node start, end_;
queue<node> q;

/**
 * 更新食人花的时间
 * 
 * 如果时间>0，减一，否则不变
*/
int updateftime(int ft)
{
    if(ft > 0)
        ft -= 1;
    return ft;
}

/**
 * 新节点判定函数
 * 
 * 如果x、y或遇到墙或时间超了，返回false
 * 更新食人花时间
 * 如果遇到食人花：1.此时食人花时间>0，吃掉食人花，时间置-1
 *               2.此时食人花时间=0，被食人花吃掉，时间置t
 *               3.此时食人花时间=-1，已经没有食人花，时间置-1
 * 
 * 判断节点是否用过
 * 如果没走过，used置1，alltime+1返回
*/
node newplace(node now, int i)
{
    node next;
    next.x = now.x + nextstep[i][0], next.y = now.y + nextstep[i][1], next.ftime = now.ftime;
    if(next.x < 1 || next.x > m || next.y < 1 || next.y > n || maze[next.x][next.y] == '#' || now.alltime >= p)
    {
        next.useful = false;
        return next;
    }
    next.ftime = updateftime(now.ftime);
    if(maze[next.x][next.y] == '@')
    {
        if(next.ftime > 0)
            next.ftime = -1;
        else if(next.ftime == 0)
            next.ftime = t, next.x = start.x, next.y = start.y;
        else
            next.ftime = -1;
    }
    if(used[next.x][next.y][next.ftime] == 1)
    {
        next.useful = false;
        return next;
    }
    used[next.x][next.y][next.ftime] = 1;
    next.useful = true, next.alltime = now.alltime + 1;
    return next;
}

int bfs()
{
    while(!q.empty())
    {
        node now = q.front();
        q.pop();
        for(int i = 0; i < 4; i++)
        {
            node next = newplace(now, i);
            if(next.useful)
            {
                if(next.x == end_.x && next.y == end_.y)
                    return next.alltime;
                q.push(next);
            }
        }
    }
    return -1;
}

int main()
{
    cin >> m >> n >> t >> p;
    for(int i = 1; i <= m; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            cin >> maze[i][j];
            if(maze[i][j] == '!')
                start.x = i, start.y = j, start.alltime = start.ftime = 0;
            if(maze[i][j] == '+')
                end_.x = i, end_.y = j, end_.alltime = end_.ftime = 0;
        }
    }
    q.push(start);
    used[start.x][start.y][start.ftime] = 1;
    cout << bfs();
    return 0;
}

第12关：分酒问题

描述
有一酒瓶装有8斤酒，没有量器，只有分别装5斤和3斤的空酒瓶。设计一程序将8斤酒分成两个4斤，并以最少的步骤给出答案。

输入
输入三个正整数，m、n、k，其中n+k=m，且m为偶数，表示有一个酒瓶装有m斤就，只有两个分别装n斤和k斤的空酒瓶。问最少几次能够将酒分成两个m/2斤。

输出
输出最少的次数。

输入样例
8 5 3

输出样例
7

提示
初始状态：8 0 0
1次后：3 5 0
2次后：3 2 3
3次后：6 2 0
4次后：6 0 2
5次后：1 5 2
6次后：1 4 3
7次后：4 4 0

#include 
#include 
#include 
using namespace std;

vector<int> b;     
int used[10000], step[10000], path[10000]; 
int result[100][3];   
int cap[3]; 
queue<vector<int>> q; 

/**
 * 如果当前瓶子内的酒大于交换的瓶子的剩余体积，则交换的瓶子装满，当前瓶子内酒的体积减少
 * 如果当前瓶子内的酒小于交换的瓶子的剩余体积，则酒全部装入交换的瓶子，当前瓶子为空
*/
vector<int> nextstage(vector<int> now, int i, int j)
{
    vector<int> next = now; 
    if(next[i] > (cap[j] - next[j]))
    {
        next[i] -= (cap[j] - next[j]);
        next[j] = cap[j];
    }
    else
    {
        next[j] += next[i];
        next[i] = 0;
    }
    return next;
}

/**
 * 对于当前瓶子，如果不为空，则遍历剩下两个瓶子进行酒的交换（利用(i + j) % 3）
 * i为当前瓶子，j为与之相交换的瓶子
 * 
 * 注释掉的代码为输出每次交换后三个瓶子体积的状态函数
*/
void bfs()
{  
    while(!q.empty()){
        vector<int> now = q.front();
        q.pop();
        for(int i = 0; i < 3; i++)
        {
            if(now[i] != 0)
            {
               for(int j = 1; j < 3; j++)
               {
                    vector<int> next = nextstage(now, i, (i + j) % 3);
                    if(!used[next[0] * 100 + next[1] * 10 + next[2]])
                    {
                        step[next[0] * 100 + next[1] * 10 + next[2]] = step[now[0] * 100 + now[1] * 10 + now[2]] + 1;
                        //path[next[0] * 100 + next[1] * 10 + next[2]] = now[0] * 100 + now[1] * 10 + now[2];
                        if(next[0] == cap[0] / 2 && next[1] == cap[0] / 2)
                            return;

                        q.push(next);
                        used[next[0] * 100 + next[1] * 10 + next[2]] = 1;
                    }
               }
            }
        }
    }
    return ;
}

/*
void dispath()
{
    int count = step[(cap[0] / 2) * 110];
    result[count][2] = 0, result[count][1] = cap[0] / 2, result[count][0] = cap[0] / 2; 
    int wine = path[(cap[0] / 2) * 110];
    for(int i = count - 1; i > 0; i--)
    {
        result[i][2] = wine % 10, result[i][1] = (wine / 10) % 10, result[i][0] = wine / 100; 
        wine = path[wine];
    }
    for(int i = 1; i <= count; i++)
        cout << "第" << i << "次:" << result[i][0] << " " << result[i][1] << " " << result[i][2] << endl;
}
*/

int main()
{
    cin >> cap[0] >> cap[1] >> cap[2];
    used[cap[0] * 100] = 1, path[cap[0] * 100] = 0;
    b.push_back(cap[0]), b.push_back(0), b.push_back(0);
    q.push(b);
    bfs();
    cout << step[(cap[0] / 2) * 110];
    //dispath();
    return 0;
}