（二）NLP-中文分词-HMM-维特比算法
中文分词
一、词
词是一个完整语义的最小单位。分词技术是词性标注、命名实体识别、关键词提取等技术的基础。
1中文分词和欧语系的分词有什么不同或者说是难点的呢？
主要难点在于汉语结构与印欧体系语种差异甚大，对词的构成边界方面很难进行界定。
比如，在英语中，单词本身就是“词”的表达，一篇英文文章就是“单词”加分隔符(空格)来表示的，而在汉语中，词以字为基本单位的，但是一篇文章的语义表达却仍然是以词来划分的。因此，在处理中文文本时，需要进行分词处理，将句子转化为词的表示。这个切词处理过程就是中文分词，是通过计算机自动识别出句子的词，在词间加入边界标记符，分隔出各个词汇。整个过程看似简单，然而实践起来却很复杂，主要的困难在于分词标准、切分歧义和未登录词三部分。
（1）分词标准
比如人名，有的算法认为姓和名应该分开，有的认为不应该分开。这需要制定一个相对统一的标准。又例如“花草”，有的人认为是一个词，有的人认为应该划分开为两个词“花/草”。某种意义上，中文分词可以说是一个没有明确定义的问题。
（2）切分歧义
不同的切分结果会有不同的含义，这又包含如下几种情况：
1）组合型歧义：
分词粒度不同导致的不同切分结果。这种问题需要根据使用场景来选择。在文本分类，情感分析等文本分析场景下，粗粒度划分较好。
2）交集型歧义：
不同切分结果共用相同的字，前后组合的不同导致不同的切分结果。这也需要通过整句话来区分。交集型歧义前后组合，变化很多，难以预测，故也有专家称之为“偶发型歧义”。
3）真歧义：
本身语法或语义没有问题，即使人工切分也会产生歧义。此时通过整句话还没法切分，只能通过上下文语境来进行切分。有专家统计过，中文文本中的切分歧义出现频次为1.2次/100汉字，其中交集型歧义和组合型歧义占比为12:1。而对于真歧义，一般出现的概率不大。
（3）未登录词
未登录词也叫新词发现，或者生词，未被词典收录的词。未登录词分为如下几种类型：
1）.新出现的词汇，比如一些网络热词。
2）.专有名词，主要是人名、地名、组织机构。
3）.专业名词和研究领域词语。
4）.其他专有名词，比如新出现的电影名、产品名、书籍名等。
未登录词对于分词精度的影响远远超过歧义切分。未登录词识别难度也很大，主要原因有：
1）. 未登录词增长速度往往比词典更新速度快很多，因此很难利用更新词典的方式解决未登录词问题。不过词典越大越全，分词精度也会越高。因此一个大而全的词典还是相当重要的。
2）. 未登录词都是由普通词汇构成，长度不定，也没有明显的边界标志词
3）. 未登录词还有可能与上下文中的其他词汇构成交集型歧义。
4）. 未登录词中还有可能夹杂着英语字母等其他符号，这也带来了很大难度。比如“e租宝”。对于词典中不包含的未登录词，我们无法基于字符串匹配来进行识别。此时基于统计的分词算法就可以大显身手了，jieba分词采用了HMM隐马尔科夫模型来解决未登录词问题。
二、中文分词方法
自中文自动分词被提出以来，历经将近30年的探索，提出了很多方法，可主要归纳为：
1.规则分词
2.统计分词
3.混合分词(规则+统计）
规则分词是最早兴起的方法，主要是通过人工设立词库，按照一定方式进行匹配切分，其实现简单高效，但对新词很难进行处理。随后统计机器学习技术的兴起，就有了统计分词，能够较好应对新词发现等特殊场景。然而实践中，单纯的统计分词也有缺陷，那就是太过于依赖语料的质量，因此实践中多是采用这两种方法的结合，即混合分词。
1、规则分词
基于规则的分词是一种机械分词方法，主要是通过维护词典，在切分语句时，将语句的每个字符串与词表中的词进行逐一匹配，找到则切分，否则不予切分。按照匹配切分的方式，主要有正向最大匹配法、逆向最大匹配法以及双向最大匹配法三种方法。
（1）规则分词–正向最大匹配法
正向最大匹配(Maximum Match Method, MM法)的基本思想为：
1. 假定/分词/词典/中的最长词有i个汉字字符，则用被处理文档的当前字串中的前i个字作为匹配字段，查找字典。
2. 若字典中存在这样的一个i字词，则匹配成功，匹配字段被作为一个词切分出来。
3. 如果词典中找不到这样的一个i字词，则匹配失败，将匹配字段中的最后一个字去掉，对剩下的字中重新进行匹配处理。
**4.**如此进行下去，直到匹配成功，即切分出一个词或剩余字串的长度为零为止。
**5.**这样就完成了一轮匹配，然后取下一个i字字串进行匹配处理，直到文档被扫描完为止。
（2）规则分词—逆向最大匹配法
逆向最大匹配(Reverse Maximum Match Method,RMM法)的基本原理与MM法相同，不同的是分词切分的方向与MM法相反。
逆向最大匹配法从被处理文档的末端/开始/匹配/扫描，每次取最末端的i个字符(i为词典中最长词的字数)作为匹配字段，若匹配失败，则去掉匹配字段最前面的一个字，继续匹配。
相应地，它使用的分词词典是逆序词典，其中的每个词条都将按逆序方式存放。在实际处理时，先将文档进行倒排处理，生成逆序文档。然后，根据逆序词典，对逆序文档用正向最大匹配法处理即可。由于汉语中偏正结构较多，若从后向前匹配，可以适当提高精度。所以，逆向最大匹配法比正向最大匹配法的误差要小。统计结果表明，单纯使用正向最大匹配的错误率为1/169，单纯使用逆向最大匹配的错误率为1/245。
（3）规则分词–双向最大匹配法
双向最大匹配法(Bidirectction Matching method)是将正向最大匹配法得到的分词结果和逆向最大匹配法得到的结果进行比较，然后按照最大匹配原则，选取词数切分最少的作为结果。
研究表明，中文中90.0%左右的句子，正向最大匹配法和逆向最大匹配法完全重合且正确，只有大概9.0%的句子两种切分方法得到的结果不一样，但其中必有一个是正确的，只有不到1.0%的句子，使用正向最大匹配法和逆向最大匹配法的切分虽重合却是错的，或者正向最大匹配法和逆向最大匹配法切分不同但两个都不对。这正是双向最大匹配法在实用中文信息处理系统中得以广泛使用的原因。
2、统计分词
随着大规模语料库的建立，统计机器学习方法的研究与发展，基于统计的中文分词算法渐渐成为主流。
其主要思想是把每个词看做是由词的最小单位的各个字组成的，如果相连的字在不同的文本中出现的次数越多，就证明这相连的字很可能就是一个词。因此我们就可以利用字与字相邻出现的频率来反应成词的可靠度，统计语料中相邻共现的各个字的组合的频度，当组合频度高于某一个临界值时，我们便可认为此字组可能会构成一个词语。
基于统计的分词算法，本质上是一个序列标注问题。我们将语句中的字，按照他们在词中的位置进行标注。标注主要有：B（词开始的一个字），E（词最后一个字），M（词中间的字，可能多个），S（一个字表示的词）。
例如：
“网商银行是蚂蚁金服微贷事业部的最重要产品”，
标注后结果为：
“BMME/S/BMMEBMMMESBMEBE”，
对应的分词结果为：
“网商银行/是/蚂蚁金服/微贷事业部/的/最重要/产品”。
（1）统计分词–HMM模型
隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。
用x表示状态，
y表示观察值
假设观察到的结果为Y:Y=y(0)，y(1)，…，y(L-1)
隐藏条件为X:X=x(0)，x(1)，…，x(L-1)
长度为L，则马可夫模型的概率可以表达为：
用一个例子说明HMM模型：
假设有三个不同的骰子。第一个骰子是平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。
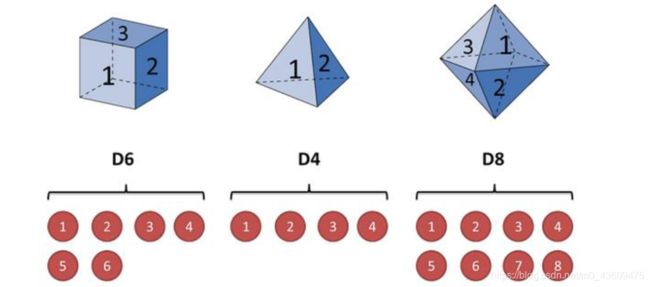开始掷骰子：
1. 先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。
2. 然后我们掷骰子，得到数字1，2，3，4，5，6，7，8中的一个。
3. 不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4这串数字叫做可见状态链（对应上面公式的观察到的结果为Y）。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链（对应上面公式的隐藏的为X）。在这个例子里，这串隐含状态链就是所用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8。
一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。一般情况权重设定也确实是不一样的（一个状态到另一个状态之间转换概率是不同的）。同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability），即由隐含状态产生可见状态的概率。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。
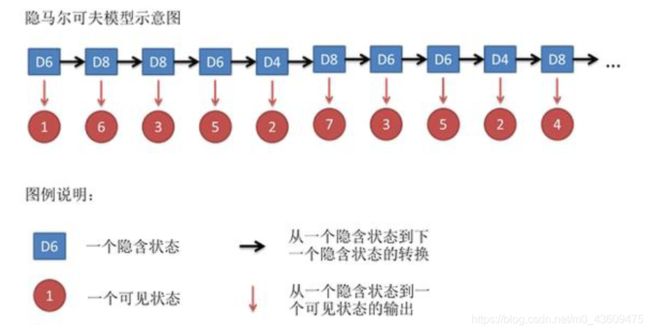
而三个骰子之间也是可以相互转换的：
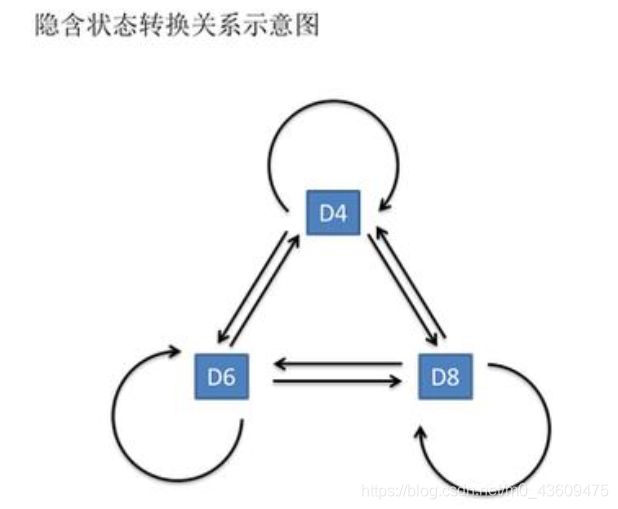
其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用HMM模型时候，往往是缺失了一部分信息的。有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你只是看到了很多次掷骰子的结果，剩下的什么都不知道。如何应用算法去估计这些缺失的信息，就成了一个很重要的问题。
与HMM模型相关的算法，算法分为三类，分别对应着解决三种问题：
1.评估问题： 知道骰子有几种（隐含状态数量），每种骰子向另一种骰子转换的概率（转换概率），根据掷骰子掷出的结果（可见状态链），想知道掷出这个结果的概率。（知道所有信息 求某个输出的可见序列的概率）
2.解码问题： 知道骰子有几种（隐含状态数量），每种骰子向另一种骰子转换的概率（转换概率），根据掷骰子掷出的结果（可见状态链），想知道每次掷出来的都是哪种骰子（隐含状态链）。（求隐含状态链）
3.学习问题： 知道骰子有几种（隐含状态数量），不知道每种骰子向另一种骰子转换的概率（转换概率），观测到很多次掷骰子的结果（可见状态链），想反推出每种骰子是什么（转换概率）（求转换概率）
1.计算结果
概率知道骰子有几种，每种骰子向另一种骰子转换的概率（都是1/3），每次掷的都是什么骰子，根据掷骰子掷出的结果，求产生这个结果的概率。
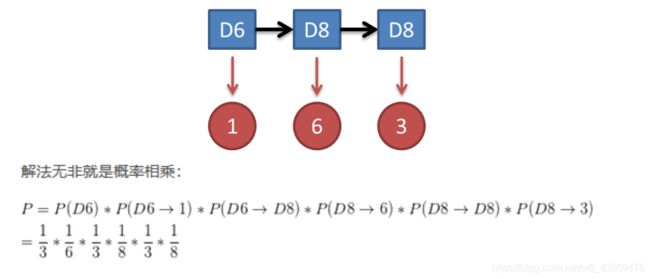
2. 计算隐含状态链
计算不可见的隐含状态概率，破解骰子序列，这里有两种解法。
2.1 解最大似然路径问题:即认为所出现的可见序列是概率最大的那的，而概率最大情况下对应得隐含状态链就是我们要找的隐含状态链
比如，我知道我有三个骰子，六面骰，四面骰，八面骰。我也知道我掷了十次的结果（1 6 3 5 2 7 3 5 2 4），我不知道每次用了那种骰子，我想知道最有可能的骰子序列。
a. 穷举所有可能的骰子序列；
b. 把每个序列对应的概率算出来；
c. 从里面把对应最大概率的序列挑出来。
如果马尔可夫链不长，当然可行。如果长的话，穷举的数量太大，就很难完成了。
2.2 维特比算法（Viterbi algorithm）：
算法思想：算法认为隐含状态链上的每一个节点为产生对应可见状态链上的节点最大概率的那个，而概率最大情况下对应得隐含状态链节点就是我们要找的隐含状态链节点。隐含节点连接起来就是隐含状态链。
举例如下：
首先，如果我们只掷一次骰子，看到结果为1。此时我们要计算这个序列的隐含状态链，计算过程如下：
1、分别计算所有状态产生结果1的概率 p(1/D4)=1/4 p(1/D6)=1/6 p(1/D8)=1/8
因为D4产生1的概率是1/4，高于1/6和1/8。所以算法认为可见状态结果1对应的隐含状态节点为D4
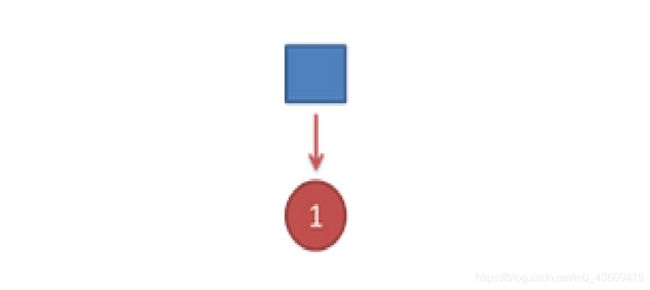
把这个情况拓展，我们掷两次骰子：结果为1，6。
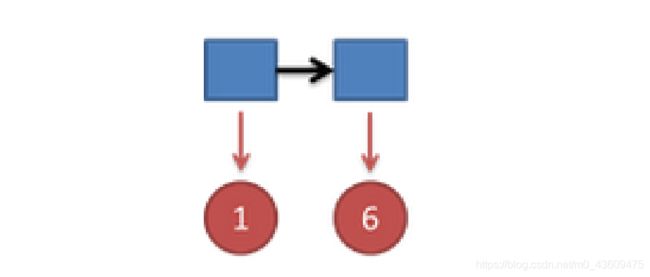
这时问题变得复杂起来，我们要计算三个值，分别是第二个骰子是D6，D4，D8
的最大概率。显然，要取到最大概率，第一个骰子必须为D4。这时，第二个骰子取到D6的最
大概率是：
同样的，我们可以计算第二个骰子是D4或D8时的最大概率。我们发现，第二个骰子取到D6的
概率最大。而使这个概率最大时，第一个骰子为D4。所以最大概率骰子序列就是D4 D6。
继续拓展，我们掷三次骰子：结果为1，6，3。
同样，我们计算第三个骰子分别是D6，D4，D8的最大概率。我们再次发现，要取到最大概
率，第二个骰子必须为D6。这时，第三个骰子取到D4的最大概率是：
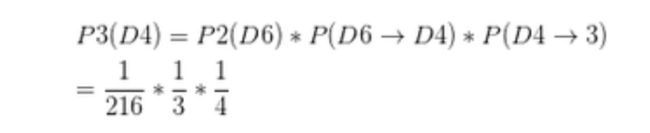
同上，我们可以计算第三个骰子是D6或D8时的最大概率。我们发现，第三个骰子取到D4的
概率最大。而使这个概率最大时，第二个骰子为D6，第一个骰子为D4。所以最大概率骰子序
列就是D4 D6 D4。
因此
我们发现，我们要求最大概率骰子序列时要做这么几件事情：
- 不管序列多长，要从序列长度为1算起，算序列长度为1时取到每个骰子的最大概率。
- 逐渐增加长度，每增加一次长度，重新算一遍在这个长度下最后一个位置取到每个骰子的最大概
率。当算到最后一位时，就知道最后一位是哪个骰子的概率最大了。 - 把对应这个最大概率的序列从后往前推出来。