二叉树OJ题目——C语言
LeetCode 104.二叉树的最大深度
1. 题目描述：
给定一个二叉树
root，返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1：
输入：root = [3,9,20,null,null,15,7] 输出：3示例 2：
输入：root = [1,null,2] 输出：2提示：
- 树中节点的数量在
[0, 104]区间内。-100 <= Node.val <= 100
OJ题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台
2. 整体思路：
首先要判断根是否存在，如果根存在，继续向下遍历，再次遍历的时候，先判断其左右子树是否存在，若存在，再遍历其左右子树，此时就不用再进行根判断了，根判断的代码只在进入函数时有效执行。
以下是我们的大致思路，但是递归的图着实太难画了，实在不理解可以仔细参照文字或者自己画
在画图的过程中我们也发现了，我们每次都要返回左右子树遍历后的较大值，如何做？
这时我们可以借用C语言库中的较大值函数，而且可以进行代码的简化：
3.解题代码：
int maxDepth(struct TreeNode* root)
{
if (root == NULL)
{
return 0;
}
return fmax(maxDepth(root->left), maxDepth(root->right)) + 1;
}LeetCode 100.相同的树
1.题目描述：
给你两棵二叉树的根节点
p和q，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。
示例 1：
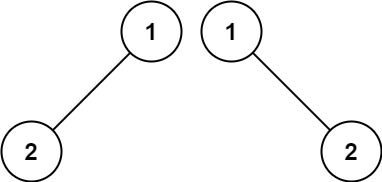
输入：p = [1,2,3], q = [1,2,3] 输出：true示例 2：
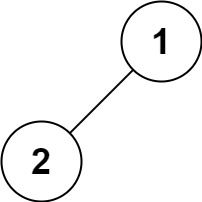
输入：p = [1,2], q = [1,null,2] 输出：false示例 3：
输入：p = [1,2,1], q = [1,1,2] 输出：false提示：
- 两棵树上的节点数目都在范围
[0, 100]内-104 <= Node.val <= 104
OJ题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台
2.整体思路：
我们先比较根，然后比较左子树，再比较右子树。
比较根时，我们要注意根的情况，如果两根都为空，或者某一根为空
当过筛后，我们才能进行递归。
3.解题代码：
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
if (p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}LeetCode 965.单值二叉树
1.题目描述：
如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时，才返回
true；否则返回false。示例 1：
输入：[1,1,1,1,1,null,1] 输出：true示例 2：
输入：[2,2,2,5,2] 输出：false提示：
- 给定树的节点数范围是
[1, 100]。- 每个节点的值都是整数，范围为
[0, 99]。
OJ题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台
2.整体思路：
我们可以考虑如何使用递归来解题，首先要考虑的肯定是父子结点的关系，我们把每棵树都分为根、左结点、右结点，在刚开始比较三者的值，若相等就继续向下递归。然后我们根据思路还加以改进判断了根的左右结点是否存在后，写了以下代码：
我们运行时测试用例正确，但提交时却报错：
原来是我们加以判断的左右子树是否存在的条件忽略了只存在一个结点且与根不一样的情况：
我们改进了代码，现在只有当子结点存在且与根结点的值相等时才会进行递归。
3.解题代码：
bool isUnivalTree(struct TreeNode* root)
{
if (root == NULL)
return true;
if (root->left && root->left->val != root->val)
return false;
if (root->right && root->right->val != root->val)
return false;
bool leftans = isUnivalTree(root->left);
bool rightans = isUnivalTree(root->right);
return leftans && rightans;
}LeetCode 144.二叉树的前序遍历
1.题目描述：
给你二叉树的根节点
root，返回它节点值的 前序 遍历。示例 1：
输入：root = [1,null,2,3] 输出：[1,2,3]示例 2：
输入：root = [] 输出：[]示例 3：
输入：root = [1] 输出：[1]示例 4：
输入：root = [1,2] 输出：[1,2]示例 5：
输入：root = [1,null,2] 输出：[1,2]提示：
- 树中节点数目在范围
[0, 100]内-100 <= Node.val <= 100
2.整体思路：
我们先来看他代码区的代码，其实还是能发现一点端倪的，这和我们之前写的前序遍历大不相同，这道OJ题需要一个返回值，他要求我们放到数组里面。
然而数组应该开多大呢？returnSize其实并非是题者给我们的提示，所以我们需要遍历二叉树自己找到二叉树的结点个数，这就用到了二叉树中求结点个数的函数：
然后我们看到returnSize，我们先来解释一下啊returnSize的意思：它并不是题者给我们的提示，在LeetCode中，当需要我们malloc来返回数组时，通常参数都会给我们配returnSize，在我们的代码中我们需要修改returnSize的值，以此让OJ后台能遍历我们的数组。
我们来写一个把值存放入数组的前序遍历函数，其实和前序遍历的区别就是不打印而存入数组。
最后，在我们的主函数中，我们只需要调用上述函数并将存入数组的下标传入即可：
3.解题代码：
int TreeSize(struct TreeNode* root)
{
if(root == NULL)
return 0;
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
void Preorder(struct TreeNode* root, int* a, int* p)
{
if(root == NULL)
return;
a[*p] = root->val;
(*p)++;
Preorder(root->left, a, p);
Preorder(root->right, a, p);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
int size = TreeSize(root);
int* a = (int*)malloc(sizeof(int) * size);
*returnSize = size;
int i = 0;
Preorder(root, a, &i);
return a;
}LeetCode 226.翻转二叉树
1.题目描述：
给你一棵二叉树的根节点
root，翻转这棵二叉树，并返回其根节点。示例 1：
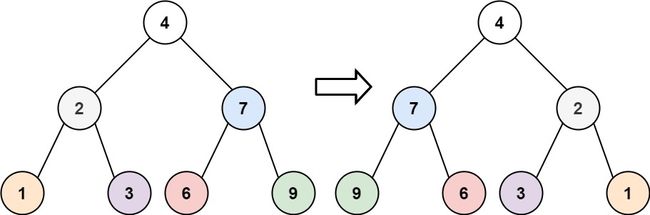
输入：root = [4,2,7,1,3,6,9] 输出：[4,7,2,9,6,3,1]示例 2：
输入：root = [2,1,3] 输出：[2,3,1]示例 3：
输入：root = [] 输出：[]提示：
- 树中节点数目范围在
[0, 100]内-100 <= Node.val <= 100
OJ题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台
2.整体思路：
我们看图可以发现这题仍然使用递归的思路，当根为空时返回，根不为空交换子树。
我们可以写一个Swap，来交换左右子树，也可以直接更改左右子树的指向。
如果要写一个Swap函数，因为我们交换的是左右结点的地址，所以我们传参要用二级指针。
3.解题代码：
void Swap(struct TreeNode** left, struct TreeNode** right)
{
struct TreeNode* ret = *left;
*left = *right;
*right = ret;
}
struct TreeNode* invertTree(struct TreeNode* root)
{
if (root == NULL)
return NULL;
Swap(&root->left, &root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}LeetCode 572.另一棵树的子树
1.题目描述：
给你两棵二叉树
root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在，返回true；否则，返回false。二叉树
tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。示例 1：
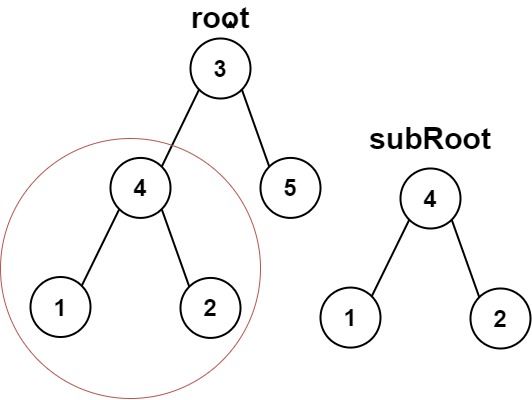
输入：root = [3,4,5,1,2], subRoot = [4,1,2] 输出：true示例 2：
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 输出：false提示：
root树上的节点数量范围是[1, 2000]subRoot树上的节点数量范围是[1, 1000]-104 <= root.val <= 104-104 <= subRoot.val <= 104
OJ题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台
2.整体思路：
这题一看就能用到 100.相同的树 中的代码，我们拷贝一份isSameTree的代码放在上面：
首先，我们先从根开始判断两者是否相同：
如果root和subRoot不相同怎么办？我们继续调用isSubtree，直到两者相同。
当根的isSameTree或左右子树的isSubTree有一为真时，我们就返回真值：
当我们提交代码时，会发现第二个用例出错了，原因是因为我们输出了true，原因是因为我们的bool类型没有初值时都为真，所以一开始我们需要把ret赋值为false：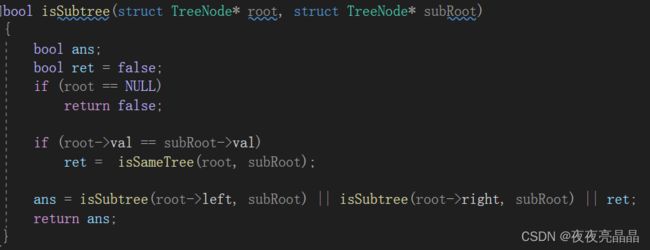
即可解决。
3.解题代码：
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
if (p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
bool ans;
bool ret = false;
if (root == NULL)
return false;
if (root->val == subRoot->val)
ret = isSameTree(root, subRoot);
ans = isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot) || ret;
return ans;
}