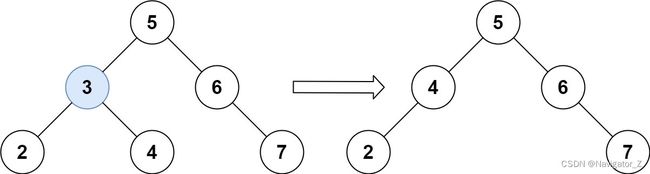
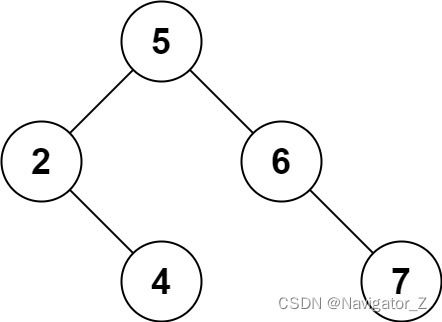
- 暑假训练.2
zz1342315890
暑假acm训练acm训练
因为网络,上午都没写成题,太伤心了。下午的时候,才去写题。今天的题对于我来说,真的好难啊。让我感觉自己差得好远啊!我应该去看看算法入门经典第二版了,光刷题,不学习也没有用啊!我知道,没有去学校集训,可能到时候参加选拔的资格也没有。但是,对于现在的我来说,不得不待在家里面。没什么,好好学习!
- 摄影测量后方交会算法C#实现
安平桥
C#摄影测量后方交会
界面设计控制点PID,x(mm),y(mm),X(m),Y(m),Z(m)1,-86.15,-68.99,36589.41,25273.32,2195.172,-53.4,82.21,37631.08,31324.51,728.693,-14.78,-76.63,39100.97,24934.98,2386.54,10.46,64.43,40426.54,30319.81,757.31导入数据Op
- 目标检测中的标签分配算法总结
北京地铁1号线
目标检测与图像处理人工智能
目标检测中的标签分配算法是训练过程中的一个核心环节,它决定了如何将标注好的真实目标框分配给模型预测出来的候选框(AnchorBoxes或Points),从而为这些候选框提供监督信号(正样本、负样本、忽略样本)。它的质量直接影响模型的学习效率和最终性能。简单来说,标签分配要解决的关键问题是:“哪些预测框应该负责学习哪些真实目标?”一、为什么标签分配如此重要?1.定义学习目标:它直接告诉模型哪些预测应
- 代码随想录算法训练营总结篇
m0_74934708
算法
第一次接触卡哥的课程是在大二上,当时做N皇后的题目看到卡哥的视频觉得大受裨益,就想着有时间能够刷完卡哥录制的整期课程,后面有算法训练营的监督让我很幸运地坚持了六十天,学到了很多东西,像贪心算法、动态规划、单调栈以及在二叉树里使用BFS和DFS,都是一些很美妙的思路。这次一刷leetcode后面要去学学前端了,等到暑假有时间希望可以跟着卡哥二刷leetcode。学会算法后再去做题有些痛苦,但做出来的
- 图论篇--代码随想录算法训练营第五十九天打卡|Bellman_ford 算法精讲,SPFA算法,Bellman ford之判断负权回路,Bellman ford之单源有限最短路
無量空所
leetcode算法图论c++
本系列算法用来解决有负权边的情况Bellman_ford算法精讲题目链接:94.城市间货物运输I题目描述:某国为促进城市间经济交流,决定对货物运输提供补贴。共有n个编号为1到n的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本-政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用
- 【前端vue3面试题】2024最新面试实录vue3(2),最新前端大厂高频面试题
*watch与watchEffect*provide与inject重构虚拟DOM,diff算法生命周期更名beforeDestroy改名为beforeUnmountdestroyed改名为unmounted//Vue3.0也提供了CompositionAPI形式的生命周期钩子,与Vue2.x中钩子对应关系如下:beforeCreate===>setup()created===>setup()bef
- MATLAB 基于图像处理的杂草识别技术
鱼弦
matlab图像处理计算机视觉
MATLAB基于图像处理的杂草识别技术1.系统介绍杂草识别是精准农业中的重要环节,基于图像处理的杂草识别技术利用计算机视觉和机器学习算法,自动识别田间杂草,为精准施药提供决策支持。本系统基于MATLAB实现杂草图像处理,包括图像预处理、特征提取、分类识别等模块。2.应用场景精准农业:自动识别田间杂草,实现精准施药,减少农药使用量。生态监测:监测农田杂草种类和分布,评估生态环境。植物保护:识别有害杂
- 维基框架发布 1.0.11 至中央仓,深化国产化 DevOps 生态整合
维基框架
维基框架springbootspringcloudmybatis架构
一、核心事件:维基框架1.0.11正式入驻中央仓库维基框架(Wiki-Framework)作为国产全场景Java企业级开发框架,于7月9日正式发布v1.0.11版本至中央软件仓库(MavenCentral),标志着其正式纳入全球主流开发工具生态。本次发布聚焦安全增强与云原生适配:安全升级:集成OAuth2.1协议,修复CVE-2025-0113等5项高危漏洞,支持国密算法SM4加密通信。云原生支持
- Python 机器学习:NumPy 实现朴素贝叶斯分类器
Python编程之道
Python编程之道python机器学习numpyai
Python机器学习:NumPy实现朴素贝叶斯分类器关键词:朴素贝叶斯分类器、NumPy、机器学习、概率模型、条件概率、拉普拉斯平滑、向量化计算摘要:本文系统讲解朴素贝叶斯分类器的核心原理,基于NumPy实现高效的算法框架,涵盖从概率理论到工程实现的完整流程。通过数学公式推导、代码实现和鸢尾花数据集实战,展示如何利用向量化计算优化概率估计,解决特征独立性假设下的分类问题。同时分析算法优缺点及实际应
- 代码随想录算法训练营第二十二天
天天开心(∩_∩)
算法深度优先
LeetCode.77组合题目链接组合题解classSolution{List>result=newArrayListpath=newLinkedList>combine(intn,intk){dfs(n,k,1);returnresult;}publicvoiddfs(intn,intk,intcount){if(path.size()==k){result.add(newArrayList>r
- 代码随想录算法训练营第二十三天
天天开心(∩_∩)
算法
LeetCode.39组合总和题目链接组合总和题解classSolution{List>resList=newArrayList>();Listres=newArrayList>combinationSum(int[]candidates,inttarget){if(candidates==null||candidates.length==0){returnresList;}Arrays.sort
- 代码随想录算法训练营第二十四天
天天开心(∩_∩)
算法深度优先
LeetCode.93复原IP地址题目链接复原IP地址题解classSolution{ListresList=newArrayList();Listres=newArrayList();publicListrestoreIpAddresses(Strings){if(s.length()==0)returnresList;dfs(s,0);returnresList;}publicvoiddfs(
- 代码随想录算法训练营第十七天
天天开心(∩_∩)
算法数据结构
目录LeetCode.654最大二叉树题目链接最大二叉树题解解题思路LeetCode.617合并二叉树题目链接合并二叉树题解解题思路LeetCode.700二叉搜索树中的搜索题目链接二叉搜索树中的搜索题解解题思路解题思路LeetCode.98验证二叉搜索树题目链接验证二叉搜索树题解解题思路解题思路总结与收获LeetCode.654最大二叉树题目链接最大二叉树题解classSolution{publ
- MATLAB实现基于多目标粒子群优化算法(MOPSO)进行无人机三维路径规划的详细项目实例
nantangyuxi
MATLABmatlab算法无人机人工智能深度学习机器学习数据挖掘
目录MATLAB实她基她她目标粒子群优化算法(MOPSO)进行无人机三维路径规划她详细项目实例1项目背景介绍...1项目目标她意义...2优化无人机飞行路径她安全她...2提升路径规划她她目标协调能力...2实她三维环境下她动态路径规划...2降低计算复杂度,实她高效路径规划...2提供具有工程实践价值她路径规划工具...3丰富她目标优化算法她应用案例...3促进无人机智能自主飞行技术进步...3
- 运维技术干货 — 不仅是 Linux 运维最佳实践
python算法小白
Linux
附Java/C/C++/机器学习/算法与数据结构/前端/安卓/Python/程序员必读书籍书单大全:书单导航页(点击右侧极客侠栈即可打开个人博客):极客侠栈①【Java】学习之路吐血整理技术书从入门到进阶最全50+本(珍藏版)②【算法数据结构+acm】从入门到进阶吐血整理书单50+本(珍藏版)③【数据库】从入门到进阶必读18本技术书籍网盘吐血整理网盘(珍藏版)④【Web前端】从HTML到JS到AJ
- NOIP2013提高组复赛数据详细分析与应用指南
欧学东
本文还有配套的精品资源,点击获取简介:2013年的NOIP提高组复赛数据,涉及C++编程、算法设计、数据结构、问题分析、时间空间复杂度优化、调试测试、比赛策略、历年试题分析等多个知识点。这些数据对于参赛者、教练和信息技术教育研究者具有重要参考价值,有助于提升信息技术能力和竞赛准备的有效性。1.NOIP竞赛概览全国青少年信息学奥林匹克竞赛(NationalOlympiadinInformaticsi
- 基于深度学习的和平精英(吃鸡)内置锁头训练
摆烂仙君
深度学习人工智能
前言本教程以和平精英为例,主要讲解如何构建深度学习模型对游戏中角色进行头部标注,并控制鼠标对其进行锁定射击,同时围绕其游戏防作弊系统进行算法攻防讲解,该方案对于csgo,cf等游戏也同样适用。请注意,该教程仅供娱乐教学,若本教程评论超过100,将会开源相关代码并对实际的代码部署进行进一步分析。一、和平精英伤害机制分析在《刺激战场》(现为《和平精英》)中,击中头部的伤害远高于身体其他部位,这是由游戏
- 那些年的我们 第七十九章
梦见令狐冲
曾祥宇从李卓对陈健铭的深情里,发现原来她也有非常真诚的一面,只是她隐藏得太深,不愿意表现出来。而且李卓的那句话至少说明她不再看不起曾祥宇了。这让他对李卓的印象大为改观,而这种改观的背后,是她的话让他的自信心又有了提升。能够通过努力让别人改变对自己的看法,还是挺让他引以为豪的。李卓是从曾祥宇努力学习编程技术上改变了对他的看法。曾祥宇上学期C语言考试不及格她是知道的,也曾暗地因此更加看不起他。可是她惊
- 基于蜣螂算法优化多头注意力机制的卷积神经网络结合双向长短记忆神经网络实现温度预测DBO-CNN-biLSTM-Multihead-Attention附matlab代码
matlab科研助手
神经网络算法cnn
✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,代码获取、论文复现及科研仿真合作可私信。个人主页:Matlab科研工作室个人信条:格物致知。更多Matlab完整代码及仿真定制内容点击智能优化算法神经网络预测雷达通信无线传感器电力系统信号处理图像处理路径规划元胞自动机无人机物理应用机器学习内容介绍温度预测在气象学、农业、能源等领域具有重要的应用价值。随着大数据和人工智能技术的快速发
- 39、设计模式的实现与示例:模板方法模式
mac99
C#3.0设计模式:从入门到精通设计模式模板方法模式C#
设计模式的实现与示例:模板方法模式1.模板方法模式概述模板方法模式是一种行为型设计模式,它定义了一个算法的骨架,将某些步骤延迟到子类中实现。这样,子类可以在不改变算法结构的情况下重定义算法的某些步骤。这种模式非常适合那些有固定流程但某些步骤需要灵活调整的场景。1.1模板方法模式的特点固定的算法框架:模板方法模式定义了一个算法的框架,但在某些关键步骤上保持了灵活性。延迟实现:某些步骤被延迟到子类中实
- Python Gradio:快速搭建人脸识别应用
Python编程之道
Python人工智能与大数据Python编程之道python开发语言ai
PythonGradio:快速搭建人脸识别应用关键词:Python,Gradio,人脸识别,深度学习,计算机视觉,交互式应用,模型部署摘要:本文详细介绍了如何使用Python的Gradio库快速搭建一个交互式的人脸识别应用。我们将从基础概念出发,逐步讲解人脸识别的核心算法原理、Gradio的界面设计方法,并通过完整的项目实战演示如何将深度学习模型部署为可交互的Web应用。文章包含详细的代码实现、数
- 算法提升之字符串练习-03(KMP)
亮亮爱刷题
算法数据结构
今天给大家带来的仍是关于字符串类型的算法题目,关于这类题目,大家需要多做练习进行巩固,题型相对固定,但是比较具有思路,希望大家可以好好理解相关部分。关于KMP算法,通常有两部分组成,第一部分是通过get_next()数组求解next数组,第二部分则是通过KMP求解字符重复。第一道题:问题描述wzy给了你一个字符串,请你计算一下这个字符串最多是由多少个相同子串拼成的。注意:原串abcdabcd,则a
- 深入理解设计模式之模板模式:优雅地定义算法骨架
vvilkin的学习备忘
设计模式设计模式
在软件开发中,我们经常会遇到这样的情况:多个类执行相似的操作流程,但每个类在流程的某些步骤上有自己特定的实现。如果为每个类都完整地编写整个流程,会导致大量重复代码,且难以维护。这时候,模板模式(TemplateMethodPattern)就派上用场了。一、模板模式概述1.1什么是模板模式模板模式是一种行为型设计模式,它定义了一个操作中的算法骨架,而将一些步骤延迟到子类中实现。模板方法使得子类可以不
- 【面试必背】RAG技术全面解析:从原理到实践中的20个关键问题
大F的智能小课
人工智能语言模型python
大家好,我是大F,深耕AI算法十余年,互联网大厂核心技术岗。知行合一,不写水文,喜欢可关注,分享AI算法干货、技术心得。【专栏介绍】:欢迎关注《大模型理论和实战》、《DeepSeek技术解析和实战》,一起探索技术的无限可能!【大模型篇】更多阅读:【大模型篇】万字长文从OpenAI到DeepSeek:大模型发展趋势及原理解读【大模型篇】目前主流AI大模型体系全解析:架构、特点与应用【大模型篇】Gro
- 嵌入式学习-PyTorch(8)-day24
LGGGGGQ
学习pytorch深度学习
torch.optim优化器torch.optim是PyTorch中用于优化神经网络参数的模块,里面实现了一系列常用的优化算法,比如SGD、Adam、RMSprop等,主要负责根据梯度更新模型的参数。️核心组成1.常用优化器优化器作用典型参数torch.optim.SGD标准随机梯度下降,支持momentumlr,momentum,weight_decaytorch.optim.Adam自适应学习
- 人类的具身智能与机器的具身智能
人机与认知实验室
人类具身智能与机器具身智能的根本区别在于其基础机制和本质属性。人类具身智能是基于生物体的生理结构和神经系统的复杂交互,通过身体与环境的直接感知和体验,形成具有情感、意识和主观性的认知与行为能力。这种智能是动态的、适应性强的,并且深受个体经验、文化背景和社会互动的影响。而机器具身智能则是通过传感器、算法和数理模型来模拟与物理世界的交互,依赖于预设的规则和数据驱动的模式识别,缺乏人类的主观体验、情感和
- 基于单片机宠物喂食器/智能宠物窝/智能饲养
传送门其他作品题目速选一览表其他作品题目功能速览概述深夜加班时,你是否担心家中宠物饿肚子?出差旅途中,是否焦虑宠物无人照看?这些养宠族的共同痛点,正被一枚小小的单片机悄然化解。作为智慧宠物家居的核心设备,智能喂食器已从“定时撒粮”的机械玩具,进化成融合嵌入式控制、物联网通信、健康管理的科技终端。本文将深入拆解基于单片机的喂食器设计:从STM32主控芯片的选型,到0.5g精度的闭环投喂算法;从ESP
- 数据结构与算法学习 (08)字符串匹配--BF算法/RK算法
暱稱已被使用
BF算法也就是串的模式匹配算法,在主串中查找与模式T(副串)相匹配的子串,如果匹配成功,找到该子串在主串出现的第一个字符。模式匹配不一定是从主串第一个字符开始,可以在主串中指定起始位置。算法思想:将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种
- 【c++】提升用户体验:问答系统的交互优化实践——关于我用AI编写了一个聊天机器人……(12)
gfdhy
算法数据结构c++c语言人工智能tf-idf
本期依旧使用豆包辅助完成代码。从功能到体验的转变上个版本已经实现了问答系统的核心功能:基于TF-IDF算法的问题匹配和回答。它能够读取训练数据,处理用户输入,并返回最相关的答案。但在用户体验方面还有很大提升空间。让我们看看改进版做了哪些关键优化:1.引导系统上个版本仅在启动时显示简单的"Hello!输入'exit'结束对话。"提示,对于初次使用的用户来说不够友好。改进版增加了:详细的欢迎信息和功能
- 【C语言】基于 DEV C++的简单扫雷游戏
九.九
C语言游戏c++游戏算法c语言编辑器开发语言
目录一、代码二、实训报告三、答辩PPT一、代码这学期C语言大作业选题:基于DEVC++的简单扫雷游戏,以下是devc++适配代码。#define_CRT_SECURE_NO_WARNINGS1#include#include#include#defineROWS9#defineCOLS9#defineMINE_COUNT10voidInitBoard(charboard[][COLS],intro
- Spring中@Value注解,需要注意的地方
无量
springbean@Valuexml
Spring 3以后,支持@Value注解的方式获取properties文件中的配置值,简化了读取配置文件的复杂操作
1、在applicationContext.xml文件(或引用文件中)中配置properties文件
<bean id="appProperty"
class="org.springframework.beans.fac
- mongoDB 分片
开窍的石头
mongodb
mongoDB的分片。要mongos查询数据时候 先查询configsvr看数据在那台shard上,configsvr上边放的是metar信息,指的是那条数据在那个片上。由此可以看出mongo在做分片的时候咱们至少要有一个configsvr,和两个以上的shard(片)信息。
第一步启动两台以上的mongo服务
&nb
- OVER(PARTITION BY)函数用法
0624chenhong
oracle
这篇写得很好,引自
http://www.cnblogs.com/lanzi/archive/2010/10/26/1861338.html
OVER(PARTITION BY)函数用法
2010年10月26日
OVER(PARTITION BY)函数介绍
开窗函数 &nb
- Android开发中,ADB server didn't ACK 解决方法
一炮送你回车库
Android开发
首先通知:凡是安装360、豌豆荚、腾讯管家的全部卸载,然后再尝试。
一直没搞明白这个问题咋出现的,但今天看到一个方法,搞定了!原来是豌豆荚占用了 5037 端口导致。
参见原文章:一个豌豆荚引发的血案——关于ADB server didn't ACK的问题
简单来讲,首先将Windows任务进程中的豌豆荚干掉,如果还是不行,再继续按下列步骤排查。
&nb
- canvas中的像素绘制问题
换个号韩国红果果
JavaScriptcanvas
pixl的绘制,1.如果绘制点正处于相邻像素交叉线,绘制x像素的线宽,则从交叉线分别向前向后绘制x/2个像素,如果x/2是整数,则刚好填满x个像素,如果是小数,则先把整数格填满,再去绘制剩下的小数部分,绘制时,是将小数部分的颜色用来除以一个像素的宽度,颜色会变淡。所以要用整数坐标来画的话(即绘制点正处于相邻像素交叉线时),线宽必须是2的整数倍。否则会出现不饱满的像素。
2.如果绘制点为一个像素的
- 编码乱码问题
灵静志远
javajvmjsp编码
1、JVM中单个字符占用的字节长度跟编码方式有关,而默认编码方式又跟平台是一一对应的或说平台决定了默认字符编码方式;2、对于单个字符:ISO-8859-1单字节编码,GBK双字节编码,UTF-8三字节编码;因此中文平台(中文平台默认字符集编码GBK)下一个中文字符占2个字节,而英文平台(英文平台默认字符集编码Cp1252(类似于ISO-8859-1))。
3、getBytes()、getByte
- java 求几个月后的日期
darkranger
calendargetinstance
Date plandate = planDate.toDate();
SimpleDateFormat df = new SimpleDateFormat("yyyy-MM-dd");
Calendar cal = Calendar.getInstance();
cal.setTime(plandate);
// 取得三个月后时间
cal.add(Calendar.M
- 数据库设计的三大范式(通俗易懂)
aijuans
数据库复习
关系数据库中的关系必须满足一定的要求。满足不同程度要求的为不同范式。数据库的设计范式是数据库设计所需要满足的规范。只有理解数据库的设计范式,才能设计出高效率、优雅的数据库,否则可能会设计出错误的数据库.
目前,主要有六种范式:第一范式、第二范式、第三范式、BC范式、第四范式和第五范式。满足最低要求的叫第一范式,简称1NF。在第一范式基础上进一步满足一些要求的为第二范式,简称2NF。其余依此类推。
- 想学工作流怎么入手
atongyeye
jbpm
工作流在工作中变得越来越重要,很多朋友想学工作流却不知如何入手。 很多朋友习惯性的这看一点,那了解一点,既不系统,也容易半途而废。好比学武功,最好的办法是有一本武功秘籍。研究明白,则犹如打通任督二脉。
系统学习工作流,很重要的一本书《JBPM工作流开发指南》。
本人苦苦学习两个月,基本上可以解决大部分流程问题。整理一下学习思路,有兴趣的朋友可以参考下。
1 首先要
- Context和SQLiteOpenHelper创建数据库
百合不是茶
androidContext创建数据库
一直以为安卓数据库的创建就是使用SQLiteOpenHelper创建,但是最近在android的一本书上看到了Context也可以创建数据库,下面我们一起分析这两种方式创建数据库的方式和区别,重点在SQLiteOpenHelper
一:SQLiteOpenHelper创建数据库:
1,SQLi
- 浅谈group by和distinct
bijian1013
oracle数据库group bydistinct
group by和distinct只了去重意义一样,但是group by应用范围更广泛些,如分组汇总或者从聚合函数里筛选数据等。
譬如:统计每id数并且只显示数大于3
select id ,count(id) from ta
- vi opertion
征客丶
macoprationvi
进入 command mode (命令行模式)
按 esc 键
再按 shift + 冒号
注:以下命令中 带 $ 【在命令行模式下进行】,不带 $ 【在非命令行模式下进行】
一、文件操作
1.1、强制退出不保存
$ q!
1.2、保存
$ w
1.3、保存并退出
$ wq
1.4、刷新或重新加载已打开的文件
$ e
二、光标移动
2.1、跳到指定行
数字
- 【Spark十四】深入Spark RDD第三部分RDD基本API
bit1129
spark
对于K/V类型的RDD,如下操作是什么含义?
val rdd = sc.parallelize(List(("A",3),("C",6),("A",1),("B",5))
rdd.reduceByKey(_+_).collect
reduceByKey在这里的操作,是把
- java类加载机制
BlueSkator
java虚拟机
java类加载机制
1.java类加载器的树状结构
引导类加载器
^
|
扩展类加载器
^
|
系统类加载器
java使用代理模式来完成类加载,java的类加载器也有类似于继承的关系,引导类是最顶层的加载器,它是所有类的根加载器,它负责加载java核心库。当一个类加载器接到装载类到虚拟机的请求时,通常会代理给父类加载器,若已经是根加载器了,就自己完成加载。
虚拟机区分一个Cla
- 动态添加文本框
BreakingBad
文本框
<script> var num=1; function AddInput() { var str=""; str+="<input
- 读《研磨设计模式》-代码笔记-单例模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
public class Singleton {
}
/*
* 懒汉模式。注意,getInstance如果在多线程环境中调用,需要加上synchronized,否则存在线程不安全问题
*/
class LazySingleton
- iOS应用打包发布常见问题
chenhbc
iosiOS发布iOS上传iOS打包
这个月公司安排我一个人做iOS客户端开发,由于急着用,我先发布一个版本,由于第一次发布iOS应用,期间出了不少问题,记录于此。
1、使用Application Loader 发布时报错:Communication error.please use diagnostic mode to check connectivity.you need to have outbound acc
- 工作流复杂拓扑结构处理新思路
comsci
设计模式工作算法企业应用OO
我们走的设计路线和国外的产品不太一样,不一样在哪里呢? 国外的流程的设计思路是通过事先定义一整套规则(类似XPDL)来约束和控制流程图的复杂度(我对国外的产品了解不够多,仅仅是在有限的了解程度上面提出这样的看法),从而避免在流程引擎中处理这些复杂的图的问题,而我们却没有通过事先定义这样的复杂的规则来约束和降低用户自定义流程图的灵活性,这样一来,在引擎和流程流转控制这一个层面就会遇到很
- oracle 11g新特性Flashback data archive
daizj
oracle
1. 什么是flashback data archive
Flashback data archive是oracle 11g中引入的一个新特性。Flashback archive是一个新的数据库对象,用于存储一个或多表的历史数据。Flashback archive是一个逻辑对象,概念上类似于表空间。实际上flashback archive可以看作是存储一个或多个表的所有事务变化的逻辑空间。
- 多叉树:2-3-4树
dieslrae
树
平衡树多叉树,每个节点最多有4个子节点和3个数据项,2,3,4的含义是指一个节点可能含有的子节点的个数,效率比红黑树稍差.一般不允许出现重复关键字值.2-3-4树有以下特征:
1、有一个数据项的节点总是有2个子节点(称为2-节点)
2、有两个数据项的节点总是有3个子节点(称为3-节
- C语言学习七动态分配 malloc的使用
dcj3sjt126com
clanguagemalloc
/*
2013年3月15日15:16:24
malloc 就memory(内存) allocate(分配)的缩写
本程序没有实际含义,只是理解使用
*/
# include <stdio.h>
# include <malloc.h>
int main(void)
{
int i = 5; //分配了4个字节 静态分配
int * p
- Objective-C编码规范[译]
dcj3sjt126com
代码规范
原文链接 : The official raywenderlich.com Objective-C style guide
原文作者 : raywenderlich.com Team
译文出自 : raywenderlich.com Objective-C编码规范
译者 : Sam Lau
- 0.性能优化-目录
frank1234
性能优化
从今天开始笔者陆续发表一些性能测试相关的文章,主要是对自己前段时间学习的总结,由于水平有限,性能测试领域很深,本人理解的也比较浅,欢迎各位大咖批评指正。
主要内容包括:
一、性能测试指标
吞吐量、TPS、响应时间、负载、可扩展性、PV、思考时间
http://frank1234.iteye.com/blog/2180305
二、性能测试策略
生产环境相同 基准测试 预热等
htt
- Java父类取得子类传递的泛型参数Class类型
happyqing
java泛型父类子类Class
import java.lang.reflect.ParameterizedType;
import java.lang.reflect.Type;
import org.junit.Test;
abstract class BaseDao<T> {
public void getType() {
//Class<E> clazz =
- 跟我学SpringMVC目录汇总贴、PDF下载、源码下载
jinnianshilongnian
springMVC
----广告--------------------------------------------------------------
网站核心商详页开发
掌握Java技术,掌握并发/异步工具使用,熟悉spring、ibatis框架;
掌握数据库技术,表设计和索引优化,分库分表/读写分离;
了解缓存技术,熟练使用如Redis/Memcached等主流技术;
了解Ngin
- the HTTP rewrite module requires the PCRE library
流浪鱼
rewrite
./configure: error: the HTTP rewrite module requires the PCRE library.
模块依赖性Nginx需要依赖下面3个包
1. gzip 模块需要 zlib 库 ( 下载: http://www.zlib.net/ )
2. rewrite 模块需要 pcre 库 ( 下载: http://www.pcre.org/ )
3. s
- 第12章 Ajax(中)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Optimize query with Query Stripping in Web Intelligence
blueoxygen
BO
http://wiki.sdn.sap.com/wiki/display/BOBJ/Optimize+query+with+Query+Stripping+in+Web+Intelligence
and a very straightfoward video
http://www.sdn.sap.com/irj/scn/events?rid=/library/uuid/40ec3a0c-936
- Java开发者写SQL时常犯的10个错误
tomcat_oracle
javasql
1、不用PreparedStatements 有意思的是,在JDBC出现了许多年后的今天,这个错误依然出现在博客、论坛和邮件列表中,即便要记住和理解它是一件很简单的事。开发者不使用PreparedStatements的原因可能有如下几个: 他们对PreparedStatements不了解 他们认为使用PreparedStatements太慢了 他们认为写Prepar
- 世纪互联与结盟有感
阿尔萨斯
10月10日,世纪互联与(Foxcon)签约成立合资公司,有感。
全球电子制造业巨头(全球500强企业)与世纪互联共同看好IDC、云计算等业务在中国的增长空间,双方迅速果断出手,在资本层面上达成合作,此举体现了全球电子制造业巨头对世纪互联IDC业务的欣赏与信任,另一方面反映出世纪互联目前良好的运营状况与广阔的发展前景。
众所周知,精于电子产品制造(世界第一),对于世纪互联而言,能够与结盟