目录
高精度算法介绍
高精度算法应用
高精度加法
高精度减法
高精度乘法
高精度除法
高精度除以低精度
高精度除以高精度
高精度算法介绍
在C/C++中,我们经常会遇到限定数据范围的情况,我们先来看一下常用的int和long long两种数据类型的范围。
C++标准规定:
int占一个机器字长,在32位系统中int占32位,即4个字节,所以int的范围是[- ,
, ],为
],为 数量级。long long的范围则是[
数量级。long long的范围则是[ ,
,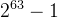 ],为
],为 数量级。如果超过该数量级,就需要用到高精度算法。
数量级。如果超过该数量级,就需要用到高精度算法。
高精度算法应用
高精度加法
1.输入两个整数a,b,输出它们的和(a,b<= )
)
直接使用int/long long进行设变量计算。
2.输入两个整数a,b,输入它们的和(a,b<= )
)
分析:int: ~
~ ,数量级为
,数量级为 ,long long:
,long long: ~
~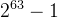 ,数量级为
,数量级为 ,解决方案:用数组模拟高精度。
,解决方案:用数组模拟高精度。
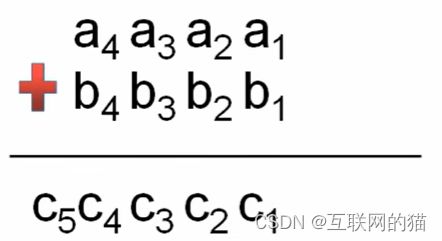 算法核心:c[i]=a[i]+b[i],c[i+1]=c[i]/10,c[i]=c[i]%10;
算法核心:c[i]=a[i]+b[i],c[i+1]=c[i]/10,c[i]=c[i]%10;
#include
#include
#include
using namespace std;
char s1[505],s2[505];
int a[505],b[505],c[505];
int main(){
int la,lb,lc;
cin>>s1>>s2;
la=strlen(s1);
lb=strlen(s2);
for(int i=0;i1){
lc--;
}
for(int i=lc;i>0;i--){
cout<
高精度减法
 要点:1.如果a
要点:1.如果a
#include
#include
#include
using namespace std;
char s1[10090],s2[10090],s3[10090];
int a[10090],b[10090],c[10090];
int flag=0;
bool compare(char s1[],char s2[]){//比较s1和s2大小
int u=strlen(s1),v=strlen(s2);
if(u!=v){
return u>v;
}
for(int i=0;is2[i];
}
}
return true;
}
int main(){
int la,lb,lc;
cin>>s1>>s2;
la=strlen(s1);
lb=strlen(s2);
if(!compare(s1,s2)){//字符交换
flag=1;//记录
strcpy(s3,s1);
strcpy(s1,s2);
strcpy(s2,s3);
//交换后也要记得交换la,lb的值
int temp=la;
la=lb;
lb=temp;
}
for(int i=0;i1){//去掉前导0
lc--;
}
if(flag==1){//交换过的最后加上负号
cout<<"-";
}
for(int i=lc;i>0;i--){
cout<
高精度乘法
 通过图示分析,我们发现规律,a[1]*b[1]对应c[1]位置,a[2]*b[1]对应c[2]位置,a[3]*b[1]对应c[3]位置,a[4]*b[1]对应c[4]位置,a[1]*b[2]对应c[2],a[2]*b[2]对应c[3]位置,a[3]*b[2]对应c[4]位置,a[4]*b[2]对应c[5]位置。
通过图示分析,我们发现规律,a[1]*b[1]对应c[1]位置,a[2]*b[1]对应c[2]位置,a[3]*b[1]对应c[3]位置,a[4]*b[1]对应c[4]位置,a[1]*b[2]对应c[2],a[2]*b[2]对应c[3]位置,a[3]*b[2]对应c[4]位置,a[4]*b[2]对应c[5]位置。
容易得出a[i]*b[j]对应c[i+j-1]位置,然后考虑进位,我们可以得到c[i+j-1]的关系式:c[i+j-1]+=a[i]*b[j];c[i+j]=c[i+j-1]/10;c[i+j-1]%=10;
#include
#include
using namespace std;
char s1[2005],s2[2005];
int a[2005],b[2005],c[4005];
int main(){
int la,lb,lc;
cin>>s1>>s2;
la=strlen(s1);
lb=strlen(s2);
for(int i=0;i1){
lc--;
}
for(int i=lc;i>0;i--){
cout<
高精度除法
高精度除以低精度
 也就是大数除以小数,使用逐位试商法(也就是不断求商和求余数的过程)
也就是大数除以小数,使用逐位试商法(也就是不断求商和求余数的过程)
#include
#include
using namespace std;
char s1[5005];//存储大数
long long b;//存储小数
long long a[5005],c[5005],la,lc,x;
int main(){
cin>>s1>>b;
la=strlen(s1);//被除数的长度
for(int i=1;i<=la;i++){
a[i]=s1[i-1]-'0';
}
for(int i=1;i<=la;i++){
c[i]=(x*10+a[i])/b;//求商
x=(x*10+a[i])%b;//求余数
}
lc=1;
while(c[lc]==0&&lc
高精度除以高精度
 方法:减法模拟除法
方法:减法模拟除法
#include
#include
using namespace std;
char s1[305],s2[305];
int a[305],b[305],c[305],tmp[305];//a为被除数,b为除数,c为商
void init(int *x){
char s[305];
cin>>s;
x[0]=strlen(s);
for(int i=0;i0;i--){
cout<b,返回0表示a=b,返回-1表示ab[0]){
return 1;
}
if(a[0]0;i--){
if(a[i]>b[i]){
return 1;
}
if(a[i]0){
a[0]--;
}//删除a的前导0,修正a的位数
}
void numcpy(int p[],int q[],int n){//将除数移动相应的位数
for(int i=1;i<=p[0];i++){
q[i+n-1]=p[i];
}
q[0]=p[0]+n-1;//移动后数组的位数
}
int main(){
init(a);//输入a
init(b);//输入b
c[0]=a[0]-b[0]+1;
for(int i=c[0];i>=1;i--){
memset(tmp,0,sizeof(tmp));
numcpy(b,tmp,i);//除数移动相应的位数
while(compare(a,tmp)>=0){//当被除数大于除数时执行循环
c[i]++;
minu(a,tmp);
}
}
while(c[c[0]]==0&&c[0]>1){
c[0]--;
}
print(c);//商
cout<
![]() ,
,![]() ],为
],为![]() 数量级。long long的范围则是[
数量级。long long的范围则是[![]() ,
,![]() ],为
],为![]() 数量级。如果超过该数量级,就需要用到高精度算法。
数量级。如果超过该数量级,就需要用到高精度算法。![]() )
)![]() )
)![]() ~
~![]() ,数量级为
,数量级为![]() ,long long:
,long long:![]() ~
~![]() ,数量级为
,数量级为![]() ,解决方案:用数组模拟高精度。
,解决方案:用数组模拟高精度。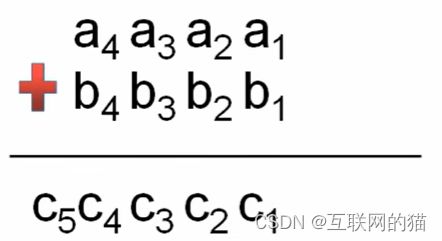 算法核心:c[i]=a[i]+b[i],c[i+1]=c[i]/10,c[i]=c[i]%10;
算法核心:c[i]=a[i]+b[i],c[i+1]=c[i]/10,c[i]=c[i]%10; 要点:1.如果a
要点:1.如果a 通过图示分析,我们发现规律,a[1]*b[1]对应c[1]位置,a[2]*b[1]对应c[2]位置,a[3]*b[1]对应c[3]位置,a[4]*b[1]对应c[4]位置,a[1]*b[2]对应c[2],a[2]*b[2]对应c[3]位置,a[3]*b[2]对应c[4]位置,a[4]*b[2]对应c[5]位置。
通过图示分析,我们发现规律,a[1]*b[1]对应c[1]位置,a[2]*b[1]对应c[2]位置,a[3]*b[1]对应c[3]位置,a[4]*b[1]对应c[4]位置,a[1]*b[2]对应c[2],a[2]*b[2]对应c[3]位置,a[3]*b[2]对应c[4]位置,a[4]*b[2]对应c[5]位置。 也就是大数除以小数,使用逐位试商法(也就是不断求商和求余数的过程)
也就是大数除以小数,使用逐位试商法(也就是不断求商和求余数的过程)