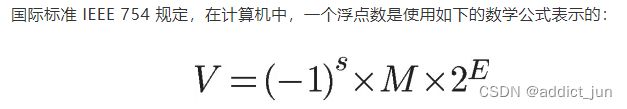C++之不同数值类型的运算及隐式转换

在C++的编写过程中，我们常常会计算不同类型之间的数据，比如long与short进行加减运算，又或者unsigned int与int之间的转换会怎么样，int与double之间的运算以及浮点类型数据是如何表示的。

这里我们来仔细的梳理一下：

废话说到这里，开始上干货

1.整形提升

问题

当整形操作数的长度小于整形的长度时，就会进行整形提升。

为什么要整形提升

因为cpu中的整形运算器ALU和通用寄存器的长度是整形的长度。所以在对char类型和short类型的数据进行处理时（在进行表达式求值时）系统会自动对这类操作数进行整形提升。

补码，反码，原码

原码：将一个整数转换成二进制形式，就是其原码。例如short a = 6;a的原码就是0000 0000 0000 0110，而a=-18，原码就是1000 0000 0001 0010。

反码：对于正数，它的反码就是其原码，负数的反码是将原码中除符号位以外的所有位取反，也就是0变成1，1变成0。例如a=-18,a的反码就是1111 1111 1110 1101。

补码：对于正数，它的补码就是其原码，负数的补码是其反码+1，例如a=-18,a的补码就是1111 1111 1110 1110。

1.小于整形长度的数据运算过程

会先进行整数提升，然后进行截断，比如char类型的数据运算。

#include
using namespace std;

int main(){

    char a = 0xb8;
    short b = 0xb800;
    int c = 0xb8000000;

    if(a == 0xb8){
        cout << "a"<<endl;
    }
    else if(b == 0xb800){
        cout << "b" << endl;
    }
    else if(c == 0xb8000000){
        cout << "c:"<<sizeof(int)<<endl;
    }
    system("pause");
    return 0;
}

输出结果

c:4

从上述例子，我们可以看出，当小于整形长度的数据进行运算的时候，会将其转化为整形之后，在进行运算，最后在进行截断操作。

2. 有符号与无符号的整数提升规则

对于有符号数，高位补符号位，（正数补0，负数补1）

//负数的整形提升
char c1 = -1;
/*
变量c1的二进制位（补码）中只有8个比特位；
11111111，即1个字节。
因为char为有符号的char
所以整数的提升的时候，高位补充符号位，结果为
11111111 11111111 11111111 11111111
*/

//正数的整形提升
char c2 = 1;
/*
变量c1的二进制位（补码）中只有8个比特位；
00000001，即1个字节。
因为char为有符号的char
所以整数的提升的时候，高位补充符号位，结果为
00000000 00000000 00000000 00000001
*/

上述为有符号整形提升。

无符号整形提升的规则较为简单，高位全补0。

3.有符号与无符号的运算规则

当有符号与无符号进行运算时，有符号会被转换成无符号在进行运算。

#include

using namespace std;

int main(){

    unsigned int a = 10;
    int b = -100;

    cout << a + b << endl;

    system("pause");
    return 0;
}

输出结果位

4294967206

这里我们结合上面说到的反码，补码，原码的知识来进行解释。

在内存中存储的整数是补码，运算也采用补码，所以

-100的补码为11111111 11111111 11111111 10011100。

10的补码为00000000 00000000 00000000 00001010。

运算结果为11111111 11111111 11111111 10100110。

转换为10进制结果为4294967206

4.整形与浮点型进行运算

在C++中，整形与浮点型运算的规则是double>float>整形的。

所以如果是double与int进行运算，则会将int转化为double，然后在进行运算。

include<iostream>

using namespace std;

int main(){

    unsigned int a = 10000;
    double b = -10.5;

    cout << a+b << endl;

    system("pause");
    return 0;
}

输出结果为

9989.5

但是这里要单独讲一下计算机中浮点型的表示方法，为什么当我们通过强转将整形转换为浮点型时，会丢失精度。

5 浮点型数据表示

• V：表示浮点型数据的值。
• S：表示符号位，这一点和整形类似。
• M：表示N的尾数位，取值在【1，2）之间，详细可以见下方float
• E：表示指数位。

float

• 第31位：符号位
• 第30-23位（8bit）：指数位，即E取值在-128~128。
• 第22-0位（23bit）：尾数位

取值范围主要看E的取值，float的范围大致在-3.4E38 — +3.4E38。

这个范围是怎么来的呢，这里我们看尾数的最大表示

0.1111111 11111111 11111111.前方在计算时，默认有一个1

接下来是指数，因为全为1的指数有特殊用途，所以最大表示为

01111111，即127。

所以按照公式则为

$(1.11111111111111111111111)\ast 2^{127}$

这里1.1111111 11111111 11111111的范围无限接近2，而不是简单的二进制转换。具体可以网上参考小数二进制与十进制的转换，这里不做解释。

故范围为：

[-3.4028235E38, 3.4028235E38]

精度主要看M，即尾数。

以int类型为例，4个字节，取值范围为[-2147483648‬, 2147483647],一共可以表示4,294,967,296种可能，我们可以理解为他可以精确表示4,294,967,296个值。

同样的，float也是4个字节，那么理论上，他最多只能精确表示4,294,967,296个值，那么为什么float的取值范围会如此大呢？因为他把间距拉大了。

//int
           [ *         *         *         0         *         *         * ]
//float
[ *          *    *    *   *  *  * * * * * 0 * * * * *  *  *   *    *    *          * ]

如果每个*表示一个数字，那么float通过这种不等间距分布，扩大了范围，也表示了小数。

饭就这么多，人多了自然不够吃了，因为远离0的位置间距越来越大，当要表示间距中间的一个数字时，只能找它附近离它最近的一个可以表示的数字来代替，这就导致了精度问题，比如我给一个float类型变量分别赋值为 4294967244 和 4294967295 ，再次输出时都变成了 4294967296，因为超过了精度，所以只能找最接近的数字代替。

从上面的分析我们已经知道，float可表示超过16777216范围的数字是跳跃的，同时float所能表示的小数也都是跳跃的，这些小数也必须能写成2的n次幂相加才可以，比如0.5、0.25、0.125…以及这些数字的和，像5.2这样的数字使用float类型是没办法精确存储的，5.2的二进制表示为101.0011001100110011001100110011……最后的0011无限循环下去，但是float最多能存储23位尾数，那么计算机存储的5.2应该是101.001100110011001100110，也就是数字 5.19999980926513671875，计算机使用这个最接近5.2的数来表示5.2。关于小数的精度与刚才的分析是一致的，当第8位有效数字发生变化时，float可能已经无法察觉到这种变化了。

double

讲完了float，那么double就是在范围和精度上得到了进一步的提升。

• 第63位：符号位
• 第62-52位（11bit）：指数位，即E取值在-1024~1024。
• 第51-0位（52bit）：尾数位

老规矩，有用二连，感谢大家！