肝了几万字,送给看了《算法图解》却是主攻Java的你和我(下篇)
有目录,不迷路
- 前言
- 第7章 迪克斯特拉算法
-
- 7.5 实现
- 第8章 贪婪算法
-
- 集合覆盖问题
-
- 近似算法
- 最后
前言
如果想看《算法图解》上半部分的Java翻译,请点击下面链接,里面还有《算法图解》电子版的百度网盘链接。嘿嘿,贴心吧!
肝了几万字,送给看了《算法图解》却是主攻Java的你和我(上篇)
第7章 迪克斯特拉算法
迪克斯特拉算法和上篇中第六章提到的广度优先搜索算法看上去差不多,其实相差很大:
- 广度优先搜索:解决最短路径问题。
- 迪克斯特拉算法:解决最快路径问题。
迪克斯特拉算法还要考虑时间因素。也就是说,在每条边上面都会有关联数字,而这些数字被称之为权重。
或者说,广度优先搜索解决的是非加权图的最短路径问题;而迪克斯特拉算法解决的是加权图的最短路径问题(即使得权重最小)。
迪克斯特拉算法总共包含4个步骤:
- 找出最便宜的节点,即可在最短时间内到达的节点。
- 更新该节点的邻居的开销,
- 重复这个过程,直到对图中每个节点都这么做了。
- 计算最终路径。
最后,请注意:
- 迪克斯特拉算法只适用于有向无环图(directed acyclic graph,DAG)。
- 迪克斯特拉算法不适用于包含负权边(即权重为负数)的图。当出现包含负权边的图时,请使用贝尔曼-福德算法(Bellman-Ford algorithm)。
以上好像说了很多废话。光说不练假把式,下面来进行实战吧:
7.5 实现
我们以下图为例,来实现迪克斯特拉算法:

如上图,各个节点之间通行的时间已经通过数字标出,求从起点到终点的最快路径!
我知道这个时候可能有小伙伴就会说了:博主呀,这个还不简单吗?简直就是小儿科呀!很明显最快路径就是:起点 — A点 — B点 — 终点,也就是总共需要花费时间为2+3+1=6;这个程你还是不要编了吧。本章结束,嘿嘿。
那本博主只能说了:非也非也!这个只是举的一个小例子,为了就是方便大家理解。待大家理解之后,自然就能够根据这个算法的核心思想去解决相关的更复杂的问题!这就是算法的妙处所在。
好了,话不多说,让我们快点开始吧!!!
按照书中的意思,我们需要三张离散表。首先,我们需要一张离散表来表示整张图:
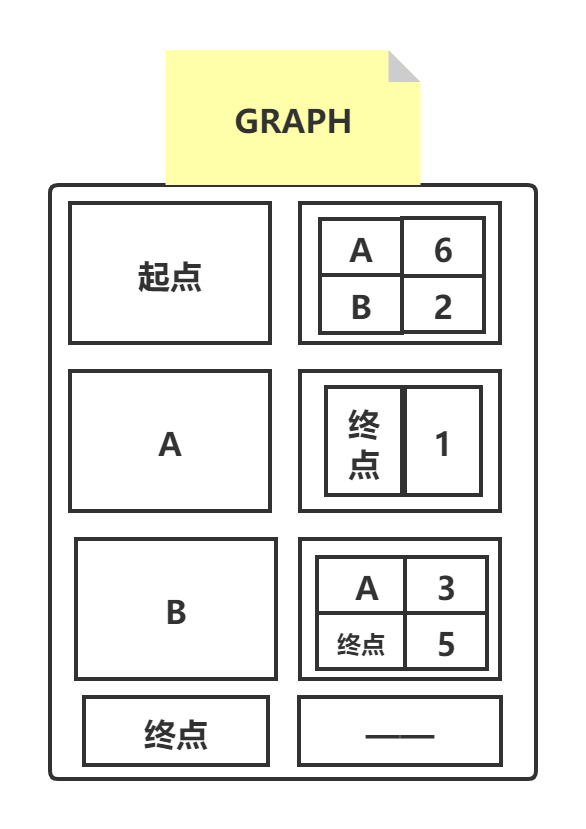
代码示例如下:
/**
* 创建图
* @param graph
*/
private static void createGraph(Map<String, Map<String, Integer>> graph) {
Map<String, Integer> start = new HashMap<String, Integer>();
start.put("a", 6);
start.put("b", 2);
graph.put("start", start);
Map<String, Integer> a = new HashMap<String, Integer>();
a.put("fin", 1);
graph.put("a", a);
Map<String, Integer> b = new HashMap<String, Integer>();
b.put("a", 3);
b.put("fin", 5);
graph.put("b", b);
graph.put("fin", null);
}
其次,我们需要一张开销表用于找到开销最小的节点:

java代码示例如下:
/**
* 创建开销表
* @param costs
*/
private static void createCosts(Map<String, Integer> costs) {
costs.put("a", 6);
costs.put("b", 2);
costs.put("fin", Integer.MAX_VALUE);
}
最后,我们需要一张记录父节点的表用于记录最短路径:
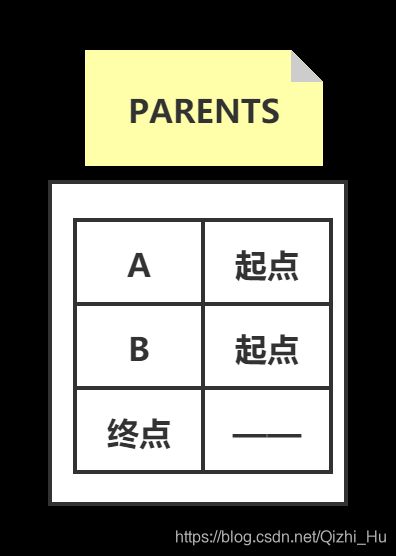
代码示例如下:
/**
* 创建一个存储父节点的散列表
* @param parents
*/
private static void createParents(Map<String, String> parents) {
parents.put("a", "start");
parents.put("b", "start");
parents.put("fin", null);
}
好的,那我们就可以用迪克斯特拉算法用Java代码实现它了:
/**
* @author guqueyue
* @Date 2020/8/3
* 迪克斯特拉算法
**/
public class Dijkstra {
public static void main(String[] args) {
// 创建图
Map<String, Map<String, Integer>> graph = new HashMap<String, Map<String, Integer>>();
createGraph(graph);
// 创建开销表
Map<String, Integer> costs = new HashMap<String, Integer>();
createCosts(costs);
// 创建一个存储父节点的散列表
Map<String, String> parents = new HashMap<String, String>();
createParents(parents);
// 寻找最快路径
dijksta(graph, costs, parents);
// 打印出最快路径
print(parents);
// 打印出最小开销
System.out.println("\n最小开销为:" + costs.get("fin"));
}
/**
* 打印出最快路径
* @param parents
*/
private static void print(Map<String, String> parents) {
List<String> node = new ArrayList<String>();
node.add("fin");
String s = parents.get("fin");
while (parents.containsKey(s)) {
node.add(s);
s = parents.get(s);
}
System.out.print("最佳路径为:start ");
for (int i = node.size() - 1; i >= 0; i--) {
System.out.print("-> " + node.get(i) + " ");
}
}
/**
* 寻找最快路径
* @param graph
* @param costs
* @param parents
*/
private static void dijksta(Map<String, Map<String, Integer>> graph, Map<String, Integer> costs, Map<String, String> parents) {
// 用于记录处理过的节点
List<String> processed = new ArrayList<String>();
// 在未处理的节点中找出开销最小的节点
String node = findLowestCostNode(costs, processed);
while (node != null) {
// 从开销表里面得到当前开销最小节点的开销
Integer cost = costs.get(node);
// 得到当前开销最小节点的邻居离散表
Map<String, Integer> neighbors = graph.get(node);
// 如果邻居离散表为空,则表明为fin即终点,则停止寻找最快路径
if (neighbors == null) return;
// 遍历当前节点的所有邻居
for (String n : neighbors.keySet()) {
// 得到前往n节点的新开销
Integer newCost = cost + neighbors.get(n);
if (newCost < costs.get(n)) { // 如果经当前节点前往该邻居更近
// 更新该邻居的开销
costs.put(n, newCost);
// 同时将该邻居的父节点设置为当前节点 -》用于回溯找出最快路径
parents.put(n, node);
}
}
// 将当前节点标记为处理过
processed.add(node);
// 找出接下来要处理的节点,并循环
node = findLowestCostNode(costs, processed);
}
}
/**
* 在未处理的节点中找出开销最小的节点
* @param costs
* @param processed
* @return
*/
private static String findLowestCostNode(Map<String, Integer> costs, List<String> processed) {
// 默认当前最小开销为Integer的最大值
Integer lowestCost = Integer.MAX_VALUE;
// 默认最小开销的节点为空
String lowestCostNode = null;
// 遍历所有的节点
for (String node : costs.keySet()) {
// 得到节点的开销
Integer cost = costs.get(node);
if (cost < lowestCost && !processed.contains(node)) { // 如果当前的节点开销更低并且没有被处理过
// 将其视为开销最低的节点
lowestCost = cost;
lowestCostNode = node;
}
}
// 返回开销最小的节点
return lowestCostNode;
}
}
第8章 贪婪算法
贪婪算法的核心理念其实很简单:即每一步都采取最优的做法。用专业术语来讲就是:每一步都选择局部最优解,进而希望最终获得一个全局最优解。当然,虽然简单易行是贪婪算法最大的优点,但是伴随而来的是它并非在任何情况下都行之有效, 并且贪婪算法获取的全局最优解其实往往也不是最优解,而只是比较优而已。
当然,有时候完美是最大的敌人。
当我们面对NP完全问题,即当情况变多、更复杂时,我们追求一个完美的答案会非常耗时难解的问题时。我们追求一个比较完美的答案就好了。代表案例有:集合覆盖问题、旅行商问题等。
下面让我们以集合覆盖问题为例,来开始实战吧!
集合覆盖问题
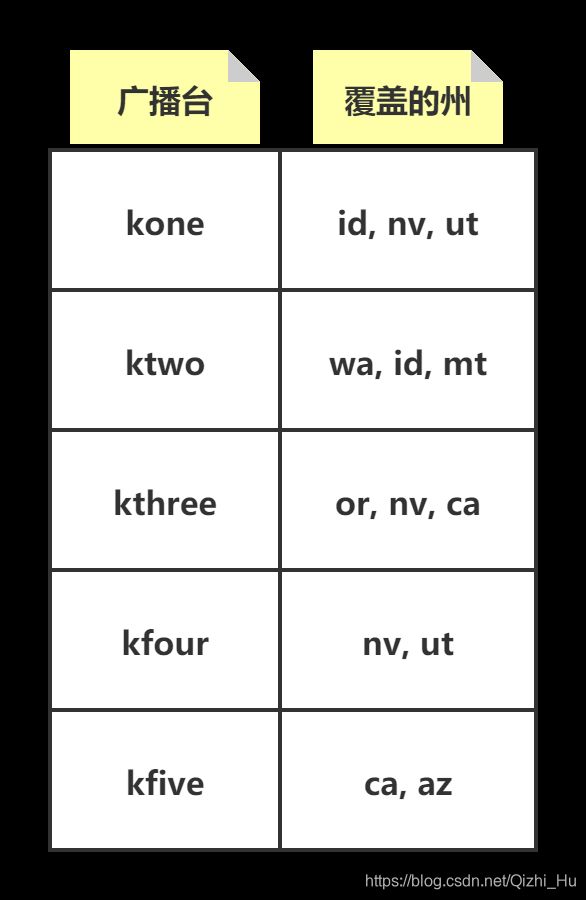
如我们办了一个广播节目,需要让美国的一些州听到这个节目,因此我们需要在广播台播出。但是天下没有白吃的午餐,在每个广播台播出都需要支付一定的费用。所以,我们需要决定在哪些广播台播出:既能让我们想收听到的州都能够收听到我们的节目,又能使得支付费用最少。
下面是我们需要让美国收听到的州:
"mt", "wa", "or", "id", "nv", "ut", "ca", "az"
近似算法
如果采用贪婪算法来解决这个集合覆盖问题 —— 广播台问题呢?其实我们只需要两步:
- 选出一个广播台,它覆盖了当前最多的未覆盖州。
- 重复第一步,直至覆盖了全部需要覆盖的州。
Java代码如下,注释很详细哦:
/**
* @author guqueyue
* @Date 2020/8/20
* 贪婪算法 - 集合覆盖问题
**/
public class Greed {
public static void main(String[] args) {
// 需要覆盖的州的数组
String[] statesArray = {"mt", "wa", "or", "id", "nv", "ut", "ca", "az"};
// 将需要覆盖的州数组转换成Set集合 - Set自带去重
Set<String> states_needed = Stream.of(statesArray).collect(Collectors.toSet());
// 用散列表表示可供选择的广播台清单 key(广播台的名称) - value(广播台覆盖的州)
Map<String, Set<String>> stations = new HashMap<>();
stations.put("kaone", new HashSet<>(Arrays.asList(new String[]{"id", "nv", "ut"})));
stations.put("kbtwo", new HashSet<>(Arrays.asList(new String[]{"wa", "id", "mt"})));
stations.put("kcthree", new HashSet<>(Arrays.asList(new String[]{"or", "nv", "ca"})));
stations.put("kdfour", new HashSet<>(Arrays.asList(new String[]{"nv", "ut"})));
stations.put("kefive", new HashSet<>(Arrays.asList(new String[]{"ca", "az"})));
// 初始化一个Set集合用于存储最终选择的广播台
Set<String> final_stations = new HashSet<>();
while (states_needed.size() > 0) {
// 最多的未覆盖州的广播台
String best_station = null;
// states_covered包含该广播台覆盖的所有未覆盖的州
Set<String> states_covered = new HashSet<>();
// 遍历广播台清单
Set<String> keys = stations.keySet();
for (String station : keys) {
// 获取广播台对应覆盖州的Set集合
Set<String> states_for_station = stations.get(station);
// 获取需要覆盖州的Set集合跟广播台覆盖州Set集合的交集
Set<String> covered = getIntersection(states_needed, states_for_station);
// 如果当前广播台覆盖 需要覆盖州的数量 大于 目前最佳广播台覆盖 需要覆盖的州的数量
if (covered.size() > states_covered.size()) {
// 则当前广播台为最佳广播台
best_station = station;
states_covered = covered;
}
}
// 从需要覆盖的州中去除已经覆盖的州
states_covered.forEach(station -> {
// 遍历移除
states_needed.remove(station);
});
// 添加目前覆盖州最多的广播台
final_stations.add(best_station);
}
// 打印最终的集合
System.out.println(final_stations);
}
/**
* 获取两个Set集合的交集
* @param states_needed
* @param states_for_station
* @return
*/
private static Set<String> getIntersection(Set<String> states_needed, Set<String> states_for_station) {
Set<String> coverd = new HashSet<>();
for (String sn : states_needed) {
for (String sfs : states_for_station) {
if (sn.equals(sfs)) {
coverd.add(sfs);
}
}
}
return coverd;
}
}
运行得:
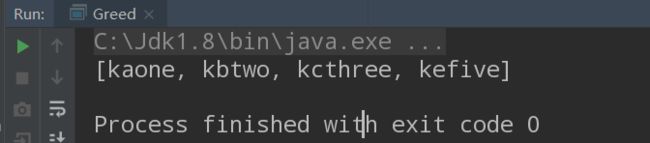
即我们选择的广播台是1、2、3、5;当然这可能不是唯一的选法,其实选择2、3、 4、5广播台同样能够解决问题!
最后
其实到了这里,整本《算法图解》就已经没有什么代码了。第九章《动态规划》以及第十章《K最近邻算法》书中只是介绍了其基本理念以及给了一些简单的伪代码。第一次写博客周期这么长,竟断断续续用了近两个月,所以这里也就不给出这两个算法的Java实现方式了。
不过,本博主以后应该会出关于动态规划算法的博客,感兴趣的可以关注我哦
在本书的最后一章《接下来如何做》中,作者并没有介绍某一种算法,而是简单介绍了10种算法:让那宏伟而又隐秘的算法地图缓缓拉开了一角。希望接下来跟大家一起加油,与诸君共勉!!!