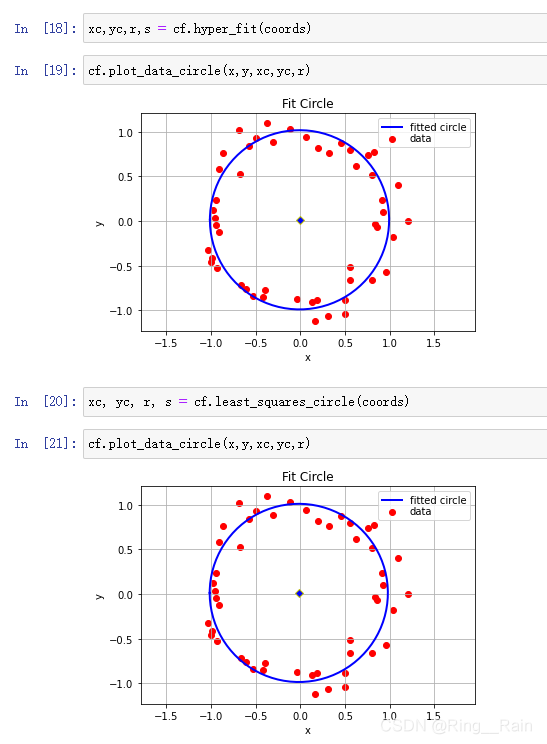
拟合圆形_
源码:https://github.com/AlliedToasters/circle-fit 已经点了个star
方法:
1,hyper_fit(超拟合方法)
2,least_squares_circle(最小二乘法)
效果
test.py
import unittest
import time
from circle_fit import hyper_fit, least_squares_circle
import numpy as np
class AppTest(unittest.TestCase):
def setUp(self):
self.startTime = time.time()
self.data = [
[329.4165297387034, 22058.59654729173],
[329.8574976938737, 22054.62783124933],
[328.9755617834489, 22051.98202025803],
[327.6526579178539, 22049.77717811104],
[326.3297510885569, 22047.57233566768],
[324.1249083488352, 22045.36749322432],
[321.9200656090292, 22043.60361962528],
[319.7152228693075, 22041.83974572986],
[317.0694121744155, 22041.39877718193],
[314.4236014794393, 22040.5168403824],
[311.7777907845473, 22040.07587183446],
[309.1319800895711, 22040.5168403824],
[305.6042334842544, 22041.39877718193],
[302.5174548341079, 22042.72168252938],
[299.8716441392159, 22044.04458787685],
[298.1077693546644, 22046.24943032021],
[296.343894570113, 22048.4542724672]
]
self.numpy_data = np.array(self.data)
def tearDown(self):
t = time.time() - self.startTime
print("%s: %.3f seconds" % (self.id(), t))
def test_hyper_fit(self):
circle = hyper_fit(self.data)
circle = hyper_fit(self.numpy_data)
def test_circle_fit(self):
circle = least_squares_circle(self.data)
circle = least_squares_circle(self.numpy_data)
if __name__ == '__main__':
unittest.main()circle_fit.py
import numpy as np
from scipy import optimize
from matplotlib import pyplot as plt, cm, colors
from math import sqrt, pi
def calc_R(x,y, xc, yc):
"""
calculate the distance of each 2D points from the center (xc, yc)
"""
return np.sqrt((x-xc)**2 + (y-yc)**2)
def f(c, x, y):
"""
calculate the algebraic distance between the data points
and the mean circle centered at c=(xc, yc)
"""
Ri = calc_R(x, y, *c)
return Ri - Ri.mean()
def sigma(coords, x, y, r):
"""Computes Sigma for circle fit."""
dx, dy, sum_ = 0., 0., 0.
for i in range(len(coords)):
dx = coords[i][1] - x
dy = coords[i][0] - y
sum_ += (sqrt(dx*dx+dy*dy) - r)**2
return sqrt(sum_/len(coords))
def hyper_fit(coords, IterMax=99, verbose=False):
"""
Fits coords to circle using hyperfit algorithm.
Inputs:
- coords, list or numpy array with len>2 of the form:
[
[x_coord, y_coord],
...,
[x_coord, y_coord]
]
or numpy array of shape (n, 2)
Outputs:
- xc : x-coordinate of solution center (float)
- yc : y-coordinate of solution center (float)
- R : Radius of solution (float)
- residu : s, sigma - variance of data wrt solution (float)
"""
X, X = None, None
if isinstance(coords, np.ndarray):
X = coords[:, 0]
Y = coords[:, 1]
elif isinstance(coords, list):
X = np.array([x[0] for x in coords])
Y = np.array([x[1] for x in coords])
else:
raise Exception("Parameter 'coords' is an unsupported type: " + str(type(coords)))
n = X.shape[0]
Xi = X - X.mean()
Yi = Y - Y.mean()
Zi = Xi*Xi + Yi*Yi
#compute moments
Mxy = (Xi*Yi).sum()/n
Mxx = (Xi*Xi).sum()/n
Myy = (Yi*Yi).sum()/n
Mxz = (Xi*Zi).sum()/n
Myz = (Yi*Zi).sum()/n
Mzz = (Zi*Zi).sum()/n
#computing the coefficients of characteristic polynomial
Mz = Mxx + Myy
Cov_xy = Mxx*Myy - Mxy*Mxy
Var_z = Mzz - Mz*Mz
A2 = 4*Cov_xy - 3*Mz*Mz - Mzz
A1 = Var_z*Mz + 4.*Cov_xy*Mz - Mxz*Mxz - Myz*Myz
A0 = Mxz*(Mxz*Myy - Myz*Mxy) + Myz*(Myz*Mxx - Mxz*Mxy) - Var_z*Cov_xy
A22 = A2 + A2
#finding the root of the characteristic polynomial
y = A0
x = 0.
for i in range(IterMax):
Dy = A1 + x*(A22 + 16.*x*x)
xnew = x - y/Dy
if xnew == x or not np.isfinite(xnew):
break
ynew = A0 + xnew*(A1 + xnew*(A2 + 4.*xnew*xnew))
if abs(ynew)>=abs(y):
break
x, y = xnew, ynew
det = x*x - x*Mz + Cov_xy
Xcenter = (Mxz*(Myy - x) - Myz*Mxy)/det/2.
Ycenter = (Myz*(Mxx - x) - Mxz*Mxy)/det/2.
x = Xcenter + X.mean()
y = Ycenter + Y.mean()
r = sqrt(abs(Xcenter**2 + Ycenter**2 + Mz))
s = sigma(coords,x,y,r)
iter_ = i
if verbose:
print('Regression complete in {} iterations.'.format(iter_))
print('Sigma computed: ', s)
return x, y, r, s
def least_squares_circle(coords):
"""
Circle fit using least-squares solver.
Inputs:
- coords, list or numpy array with len>2 of the form:
[
[x_coord, y_coord],
...,
[x_coord, y_coord]
]
or numpy array of shape (n, 2)
Outputs:
- xc : x-coordinate of solution center (float)
- yc : y-coordinate of solution center (float)
- R : Radius of solution (float)
- residu : MSE of solution against training data (float)
"""
x, y = None, None
if isinstance(coords, np.ndarray):
x = coords[:, 0]
y = coords[:, 1]
elif isinstance(coords, list):
x = np.array([point[0] for point in coords])
y = np.array([point[1] for point in coords])
else:
raise Exception("Parameter 'coords' is an unsupported type: " + str(type(coords)))
# coordinates of the barycenter
x_m = np.mean(x)
y_m = np.mean(y)
center_estimate = x_m, y_m
center, _ = optimize.leastsq(f, center_estimate, args=(x,y))
xc, yc = center
Ri = calc_R(x, y, *center)
R = Ri.mean()
residu = np.sum((Ri - R)**2)
return xc, yc, R, residu
def plot_data_circle(x, y, xc, yc, R):
"""
Plot data and a fitted circle.
Inputs:
x : data, x values (array)
y : data, y values (array)
xc : fit circle center (x-value) (float)
yc : fit circle center (y-value) (float)
R : fir circle radius (float)
Output:
None (generates matplotlib plot).
"""
f = plt.figure(facecolor='white')
plt.axis('equal')
theta_fit = np.linspace(-pi, pi, 180)
x_fit = xc + R*np.cos(theta_fit)
y_fit = yc + R*np.sin(theta_fit)
plt.plot(x_fit, y_fit, 'b-' , label="fitted circle", lw=2)
plt.plot([xc], [yc], 'bD', mec='y', mew=1)
plt.xlabel('x')
plt.ylabel('y')
# plot data
plt.scatter(x, y, c='red', label='data')
plt.legend(loc='best',labelspacing=0.1 )
plt.grid()
plt.title('Fit Circle')