LeetCode刷题笔记（Java）---第661-680题

前言

需要开通vip的题目暂时跳过

笔记导航

点击链接可跳转到所有刷题笔记的导航链接

661. 图片平滑器

包含整数的二维矩阵 M 表示一个图片的灰度。你需要设计一个平滑器来让每一个单元的灰度成为平均灰度 (向下舍入) ，平均灰度的计算是周围的8个单元和它本身的值求平均，如果周围的单元格不足八个，则尽可能多的利用它们。

• 解答

  public int[][] imageSmoother(int[][] M) {
          int R = M.length, C = M[0].length;
          int[][] ans = new int[R][C];
  
          for (int r = 0; r < R; ++r)
              for (int c = 0; c < C; ++c) {
  
                  int count = 0;
                  for (int nr = r-1; nr <= r+1; ++nr)
                      for (int nc = c-1; nc <= c+1; ++nc) {
                          if (0 <= nr && nr < R && 0 <= nc && nc < C) {
                              ans[r][c] += M[nr][nc];
                              count++;
                          }
                      }
                  ans[r][c] /= count;
                  
              }
          return ans;
      }
  

• 分析

  1. 暴力，遍历每个位置，然后在每个位置的9宫格的范围内，判断 是否超过边界，如果没有超过边界，则记录 满足边界内的格子的数量，并累积满足边界的格子内的数字和。
  2. 这一个位置的值 等于 累积的数字和 除以周围包括自身满足边界内的格子的数量。

• 提交结果

662. 二叉树最大宽度

给定一个二叉树，编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树（full binary tree）结构相同，但一些节点为空。

每一层的宽度被定义为两个端点（该层最左和最右的非空节点，两端点间的null节点也计入长度）之间的长度。

• 解答

  public int widthOfBinaryTree(TreeNode root) {
          if (root == null) return 0;
          List<TreeNode> list = new ArrayList<>();
          List<Long> index = new ArrayList<>();
          index.add((long)1);
          list.add(root);
          long res = 1;
          while (!list.isEmpty()) {
              List<TreeNode> temp = new ArrayList<>();
              List<Long> indexTemp = new ArrayList<>();
              long start = Long.MAX_VALUE;
              long end = -Long.MAX_VALUE;
              for (int i = 0; i < list.size(); i++) {
                  TreeNode node = list.get(i);
                  long ind = index.get(i);
                  start = Math.min(start, ind);
                  end = Math.max(end, ind);
                  if (node.left != null) {
                      temp.add(node.left);
                      indexTemp.add(2 * ind);
                  }
                  if (node.right != null) {
                      temp.add(node.right);
                      indexTemp.add(2 * ind + 1);
                  }
              }
              res = Math.max(res, end - start + 1);
              list = temp;
              index = indexTemp;
          }
          return (int)res;
      }
  

• 分析

  1. 对于二叉树而言，假设结点的编号为 i 那么它左孩子的结点编号为2* i 右孩子的结点编号为 2 * i + 1
  2. 层次遍历 每层记录这一层的编号 和对应的结点，然后计算这一层最大编号和最小编号的差，最大的就是最大宽度。

• 提交结果

664. 奇怪的打印机

有台奇怪的打印机有以下两个特殊要求：

1. 打印机每次只能打印同一个字符序列。
2. 每次可以在任意起始和结束位置打印新字符，并且会覆盖掉原来已有的字符。

给定一个只包含小写英文字母的字符串，你的任务是计算这个打印机打印它需要的最少次数。

• 解答

  public int strangePrinter(String s) {
          int n = s.length();
          if(n == 0) return 0;
          int[][] dp = new int[n + 1][n + 1];
  
          for(int i = 0; i < n; i++){
              dp[i][i] = 1;
          }
          for(int len = 2; len <= n; len++){
              for(int i = 0; i + len - 1 < n; i++){
                  int j = i + len - 1;
                  dp[i][j] = dp[i+1][j] + 1;
                  for(int k = i + 1; k <= j; k++){
                      if(s.charAt(i) == s.charAt(k))
                          dp[i][j] = Math.min(dp[i][j], dp[i][k - 1] + dp[k + 1][j]);
                  }
              }
          }
          return dp[0][n - 1];
      }
  

• 分析

  1. 区间DP

  2. 区间DP的套路 3层循环

     1. 区间长度
     2. 区间起点
     3. 分割点

  3. dp[i] [j] 表示 区间i～j的范围内 打印的最少次数

  4. 假设字符串i之后 不存在相同的字符 那么

     dp[i] [j] = dp[i+1] [j] + 1

  5. 遍历分割点

  6. dp[i] [j] = Math.min(dp[i] [j],dp[i] [k]+dp[k+1] [j]);

  7. 若s[k] == s[i] 那么dp[i] [k] = d[i] [k-1]

  8. 所以dp[i] [j] = Math.min(dp[i] [j],dp[i] [k-1] + dp[k+1] [j])

• 提交结果

665. 非递减数列

给你一个长度为 n 的整数数组，请你判断在 最多 改变 1 个元素的情况下，该数组能否变成一个非递减数列。

我们是这样定义一个非递减数列的： 对于数组中所有的 i (0 <= i <= n-2)，总满足 nums[i] <= nums[i + 1]。

• 解答

  public boolean checkPossibility(int[] nums) {
          // 记录是不是第一次进行改变
          boolean is = false;
          for (int i = 0; i < nums.length - 1; i++) {
              if (nums[i] > nums[i + 1]) {
                  if (is) {
                      return false;
                  }
                  // 判断是不是第一个元素
                  if (i != 0) {
                      // 如果 nums[i-1] > nums[i+1]，则将 nums[i+1] 改为 nums[i] 即可。
                      if (nums[i - 1] > nums[i + 1]) {
                          nums[i + 1] = nums[i];
                      } else {
                          // 如果 nums[i-1] <= nums[i+1]，则将 nums[i] 改为 nums[i-1]<= nums[i] <=nums[i+1] 即可。
                          nums[i] = nums[i + 1];
                      }
                  } else {
                      // 当 i = 0 时，则将 nums[i] 改为任意一个小于等于 nums[i+1] 的数即可。
                      nums[i] = nums[i + 1];
                  }
                  is = true;
              }
          }
          return true;
      }
  

• 分析

  1. 若当前 位置大于后一个位置

  2. 若是第二次出现，则说明需要修改两次 直接返回false

  3. 下面分情况

  4. 若当前位置是0，那么直接修改当前位置等于后一个位置的值

  5. 若不为0，也分两种情况

     1. 当前位置的前一个值 大于 当前位置的后一个值 例如 5 6 3

        当前是6 前一个位置是5 后一个位置是3。5大于3 此时将3修改成 6

     2. 当前位置的前一个值 小于等于当前位置的后一个值 3 6 4

        当前是6 前一个位置是3 后一个位置4，3小于4 此时将6 修改成4

• 提交结果

667. 优美的排列 II

给定两个整数 n 和 k，你需要实现一个数组，这个数组包含从 1 到 n 的 n 个不同整数，同时满足以下条件：

① 如果这个数组是 [a1, a2, a3, … , an] ，那么数组 [|a1 - a2|, |a2 - a3|, |a3 - a4|, … , |an-1 - an|] 中应该有且仅有 k 个不同整数；.

② 如果存在多种答案，你只需实现并返回其中任意一种.

• 解答

  public int[] constructArray(int n, int k) {
          int[] res = new int[n];
          int index = 0;
          int left = 1;
          int right = n;
          boolean flag = true;
          while(k > 1){
              if(flag){
                  res[index++] = left++;
              }else res[index++] = right--;
              k--;
              flag = !flag;
          }
          for(int i = index;i < n;i++){
              if(flag){
                  res[i] = left++;
              }else res[i] = right--;
          }
          return res;
      }
  

• 分析

  1. k个不同 可以假设 其中有一个是1 那么就剩下k-1个不同
  2. 整数1的结果比较简单，要么是连续的递增，要么是连续的递减
  3. k-1的不同 可以采取首尾填充的方式 例如 n = 6 k = 4
  4. 那么采用首尾填充4个点数字 得到 1 6 2 5
  5. 最后1位是5 连续递减 得到 1 6 2 5 4 3 满足题意
  6. 最后追加的连续递增还是递减，就看首尾填充的最后一位是前面拿的还是后面拿的数字。若是后面拿的数字 则后面连续递减，若是前面拿的数字则后面连续递增

• 提交结果

668. 乘法表中第k小的数

几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第k小的数字吗？

给定高度m 、宽度n 的一张 m * n的乘法表，以及正整数k，你需要返回表中第k 小的数字。

• 解答

  public int findKthNumber(int m, int n, int k) {
          int left = 1, right = m * n;
          while (left < right) {
              int mid = left + (right - left) / 2;
              if (kThCount(m, n, mid) >= k) {
                  right = mid;
              } else {
                  left = mid + 1;
              }
          }
          return left;
      }
  
      public int kThCount(int m, int n, int mid) {
          int res = 0,row = 1,col = n;
          while(row <= m && col > 0){
              if(row * col <= mid){
                  res += col;
                  row++;
              }else{
                  col--;
              }
          }
          return res;
      }
  

• 分析

  1. 二分查找
  2. 数字的范围在1 - m* n
  3. 二分查找mid在矩阵中是第几个 来缩小二分查找的范围
  4. kThCount用来计算 mid 在矩阵中是第几小的数字，也就是求有多少个数字小于等于它

• 提交结果

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构（即，如果没有被移除，原有的父代子代关系都应当保留）。 可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

• 解答

  public TreeNode trimBST(TreeNode root, int low, int high) {
          TreeNode res = root;
          root = trimBSTLow(root,low);
          return trimBSTHight(root,high);
      }
  
      public TreeNode trimBSTLow(TreeNode root,int low){
          if(root == null)return null;
          if(root.val < low){
              return trimBSTLow(root.right,low);
          }else{
              root.left = trimBSTLow(root.left,low);
          }
          return root;
      }
  
      public TreeNode trimBSTHight(TreeNode root,int high){
          if(root == null) return null;
          if(root.val > high){
              return trimBSTHight(root.left,high);
          }else{
              root.right = trimBSTHight(root.right,high);
          }
          return root;
      }
  

• 分析

  1. 递归修剪
  2. 对于左区间而言
  3. 若当前结点的值小于左区间，那么就需要将当前结点删除，替换成当前结点的右子树，然后再继续的递归的寻找。
  4. 若当前结点的值大于等于左区间，那么递归的判断左子树
  5. 对于右区间 类似

• 提交结果

670. 最大交换

给定一个非负整数，你至多可以交换一次数字中的任意两位。返回你能得到的最大值。

• 解答

  public int maximumSwap(int num) {
          String number = "" + num;
          char[] chars = number.toCharArray();
          int len = chars.length;
          char[] nums = new char[len];
          nums[len-1] = chars[len-1];
          int[] indexs = new int[len];
          indexs[len-1] = len-1;
          for(int i = len - 2;i >= 0;i--){
              if(chars[i] - '0' > nums[i+1] - '0'){
                  nums[i] = chars[i];
                  indexs[i] = i;
              }else {
                  nums[i] = nums[i+1];
                  indexs[i] = indexs[i+1];
              }
          }
          for(int i = 0;i < len;i++){
              if(chars[i] - '0' < nums[i] -'0'){
                  char temp = chars[i];
                  chars[i] = nums[i];
                  chars[indexs[i]] = temp;
                  break;
              }
          }
          return Integer.valueOf(new String(chars),10);
      }
  

• 分析

  1. 记录下当前数字后面出现的最大的数字 保存在 nums中,顺便记录对于的出现的索引位置
  2. 遍历数字的每一位，若当前位的数字 比后面出现的最大数字小，那么就和那个数字交换

• 提交结果

671. 二叉树中第二小的节点

给定一个非空特殊的二叉树，每个节点都是正数，并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话，那么该节点的值等于两个子节点中较小的一个。

更正式地说，root.val = min(root.left.val, root.right.val) 总成立。

给出这样的一个二叉树，你需要输出所有节点中的第二小的值。如果第二小的值不存在的话，输出 -1 。

• 解答

  //方法1
  public int findSecondMinimumValue(TreeNode root) {
          Set<Integer> set = new HashSet<>();
          PriorityQueue<TreeNode> queue = new PriorityQueue<>(new Comparator<TreeNode>(){
              public int compare(TreeNode node1,TreeNode node2){
                  return node1.val - node2.val;
              }
          });
          dfs(root,queue,set);
          if(queue.size() < 2)
              return -1;
          queue.poll();
          return queue.poll().val;
      }
      public void dfs(TreeNode node,PriorityQueue<TreeNode> queue,Set<Integer> set){
          if(!set.contains(node.val)){
              set.add(node.val);
              queue.add(node);
          }
          if(node.left != null){
              dfs(node.left,queue,set);
          }
          if(node.right != null){
              dfs(node.right,queue,set);
          }
      }
  //方法2
  		long ans=Long.MAX_VALUE;
      public int findSecondMinimumValue(TreeNode root) {
          if(root==null) return -1;
          int minval=root.val;
          dfs(root,minval);
          if(ans==Long.MAX_VALUE) return -1;
          return (int)ans;
      }
      private void dfs(TreeNode root, int minval) {
          if(root==null) return;
          if(root.val>minval&&root.val<ans)
              ans=root.val;
          dfs(root.left,minval);
          dfs(root.right,minval);
      }
  

• 分析

  1. 方法1利用堆来完成寻找第K个
  2. 方法2 根据根结点 得到最小值，然后遍历树寻找比它大的最小值即为答案。

• 提交结果

  方法1
  方法2

673. 最长递增子序列的个数

给定一个未排序的整数数组，找到最长递增子序列的个数。

• 解答

  //方法1
  	public int findNumberOfLIS(int[] nums) {
          if (nums == null || nums.length == 0) return 0;
          int n = nums.length;
          int[] dp = new int[n];
          int[] counter = new int[n];
          Arrays.fill(dp, 1);
          Arrays.fill(counter, 1);
          int max = 0;
          for(int i = 0; i < n; i++){
              for(int j = 0; j < i; j++) {
                  if(nums[i] > nums[j]) {
                      if(dp[j] + 1 > dp[i]) {
                          dp[i] = Math.max(dp[i], dp[j] + 1);
                          counter[i] = counter[j];
                      }else if(dp[j] + 1 == dp[i]) {
                          counter[i] += counter[j];
                      }
                  }
              }
              max = Math.max(max, dp[i]);
          }
          int res = 0;
          for(int i = 0; i < n; i++) {
              if(dp[i] == max) res += counter[i];
          }
          return res;
      }
  

• 分析

  1. 方法1 动态规划
  2. dp[i] 表示以第i个字符结尾的序列，能得到的最长上升子序列的长度
  3. count[i] 表示以第i个字符结尾的序列，满足最长上升子序列的个数
  4. 两重循环
  5. 第一重循环 遍历整个数组，每个位置作为序列的结尾
  6. 第二重循环 是0到第一重循环的位置 也就是 0-序列的结尾
  7. 若序列的结尾的数字num[i] > nums[j]
  8. 此时需要考虑两种情况 第一种是当前找到的最大上升子序列的长度 小于dp[j] + 1 说明 此时需要更新最大上升子序列的长度。并将个数 赋值为counter[j]
  9. 第二种是当前找到的最大上升子序列的长度 已经等于dp[j] + 1 此时 说明有counter[j]种情况 可以得到dp[j]+1的长度 此时需要将个数counter[i] 加上 counter[j]
  10. 第一重循环当中，还需要记录所有序列当中 最大上升子序列的长度。
  11. 最后一个for循环 遍历，找到dp[i] 等于记录下的最大上升子序列的长度对应的counter[i] 进行累加 返回结果。

• 提交结果

674. 最长连续递增序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

• 解答

  public int findLengthOfLCIS(int[] nums) {
          if(nums.length == 0)return 0;
          int last = nums[0];
          int temp = 1;
          int res = 1;
          for(int i = 1;i < nums.length;i++){
              int cur = nums[i];
              if(cur > last){
                  temp++;
                  res = Math.max(temp,res);
              }
              else temp = 1;
              last = cur;
          }
          return res;
      }
  

• 分析

  1. 连续递增 temp++ 否则 temp重置为1
  2. 记录下最大的temp 返回

• 提交结果

675. 为高尔夫比赛砍树

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示， 在这个矩阵中：

• 0 表示障碍，无法触碰
• 1 表示地面，可以行走
• 比 1 大的数 表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

• 解答

  int[] rArr = new int[]{-1, 1, 0, 0};
      int[] cArr = new int[]{0, 0, -1, 1};
  
      public int cutOffTree(List<List<Integer>> forest) {
          int rows = forest.size();
          int columns = forest.get(0).size();
          int[][] arr = new int[rows * columns][];
          int[][] grid = new int[rows][columns];
          for (int i = 0; i < forest.size(); i++) {
              for (int j = 0; j < forest.get(0).size(); j++) {
                  int height = forest.get(i).get(j);
                  arr[i * columns + j] = new int[]{i, j, height};
                  grid[i][j] = height;
              }
          }
          Arrays.sort(arr, Comparator.comparingInt(tree -> tree[2]));
          int step = 0;
          int[] src = new int[]{0, 0};
          for (int[] dest : arr) {
              if (dest[2] <= 1) {
                  continue;
              }
              int temp = bfs(src, dest, grid);
              if (temp < 0) {
                  return -1;
              }
              step += temp;
              src = dest;
          }
          return step;
      }
  
      private int bfs(int[] src, int[] dest, int[][] grid) {
          int rows = grid.length;
          int columns = grid[0].length;
          boolean[][] seen = new boolean[rows][columns];
          Queue<int[]> queue = new LinkedList<>();
          queue.add(new int[]{src[0], src[1], 0});
          while (!queue.isEmpty()) {
              int[] cur = queue.poll();
              if (cur[0] == dest[0] && cur[1] == dest[1]) {
                  return cur[2];
              }
              for (int i = 0; i < 4; i++) {
                  int nextR = cur[0] + rArr[i];
                  int nextC = cur[1] + cArr[i];
                  if (inGrid(nextR, nextC, rows, columns) && !seen[nextR][nextC] && grid[nextR][nextC] > 0) {
                      queue.add(new int[]{nextR, nextC, cur[2] + 1});
                      seen[nextR][nextC] = true;
                  }
              }
          }
          return -1;
      }
  
      private boolean inGrid(int r, int c, int maxR, int maxC) {
          return 0 <= r && r < maxR && 0 <= c && c < maxC;
      }
  

• 分析

  1. 根据树高度进行排序，
  2. 从起始点开始，利用bfs计算通往下一颗树的距离，累计。
  3. 若某一刻无法通往下一颗树 说明无法砍完所有的树，返回-1

• 提交结果

676. 实现一个魔法字典

设计一个使用单词列表进行初始化的数据结构，单词列表中的单词 互不相同 。 如果给出一个单词，请判定能否只将这个单词中一个字母换成另一个字母，使得所形成的新单词存在于你构建的字典中。

实现 MagicDictionary 类：

• MagicDictionary() 初始化对象
• void buildDict(String[] dictionary) 使用字符串数组 dictionary 设定该数据结构，dictionary 中的字符串互不相同
• bool search(String searchWord) 给定一个字符串 searchWord ，判定能否只将字符串中 一个 字母换成另一个字母，使得所形成的新字符串能够与字典中的任一字符串匹配。如果可以，返回 true ；否则，返回 false 。

• 解答

  class MagicDictionary {
      private Trie trie;
      /**
       * Initialize your data structure here.
       */
      public MagicDictionary() {
          trie = new Trie();
      }
  
      /**
       * Build a dictionary through a list of words
       */
      public void buildDict(String[] dict) {
          for (String s : dict) {
              trie.insert(s);
          }
      }
  
      /**
       * Returns if there is any word in the trie that equals to the given word after modifying exactly one character
       */
      public boolean search(String word) {
          return trie.search(word);
      }
      
      static class Trie {
          static class Node {
              boolean isWord;
              Node[] children;
  
              public Node(boolean isWord) {
                  this.isWord = isWord;
                  children = new Node[26];
              }
          }
          private Node root;
  
          public Trie() {
              this.root = new Node(false);
          }
  
          public void insert(String word) {
              Node node = root;
              for (char c : word.toCharArray()) {
                  int idx = c - 'a';
                  if (node.children[idx] == null) {
                      node.children[idx] = new Node(false);
                  }
                  node = node.children[idx];
              }
              node.isWord = true;
          }
  
          public boolean search(String word) {
              return search(word, 0, 1, root);
          }
  
          private boolean search(String word, int i, int num, Node root) {
              if (num < 0) {
                  return false;
              }
              if (i == word.length()) {
                  return num == 0 && root.isWord;
              }
              char c = word.charAt(i);
              int idx = c - 'a';
              for (int j = 0; j < 26; j++) {
                  if (root.children[j] == null) {
                      continue;
                  }
                  if (idx == j) {
                      if (search(word, i + 1, num, root.children[idx])) {
                          return true;
                      }
                  } else if (search(word, i + 1, num - 1, root.children[j])) {
                      return true;
                  }
              }
              return false;
          }
      }
  }
  

• 分析

  1. 前缀树来维护字典
  2. 题目中要求必须要更换一个字母，所以递归搜索的过程中，num来记录更换的次数
  3. 当遍历完了整个字符串，并且num == 0 当前前缀树的结点isWord标记为true 说明字符串变化了一个字母后 在前缀树中找到了匹配的结果

• 提交结果

677. 键值映射

实现一个 MapSum 类，支持两个方法，insert 和 sum：

• MapSum() 初始化 MapSum 对象
• void insert(String key, int val) 插入 key-val 键值对，字符串表示键 key ，整数表示值 val 。如果键 key 已经存在，那么原来的键值对将被替代成新的键值对。
• int sum(string prefix) 返回所有以该前缀 prefix 开头的键 key 的值的总和。

• 解答

  class MapSum {
      TrimTree trimTree;
  
      /** Initialize your data structure here. */
      public MapSum() {
          this.trimTree = new TrimTree();
      }
      
      public void insert(String key, int val) {
          TrimTree t = this.trimTree;
          for(int i = 0;i < key.length();i++){
              char cur = key.charAt(i);
              if(t.children[cur-'a'] == null){
                  t.children[cur - 'a'] = new TrimTree();
              }
              t = t.children[cur - 'a'];
          }
          t.val = val;
      }
      
      public int sum(String prefix) {
          TrimTree t = this.trimTree;
          for(int i = 0;i < prefix.length();i++){
              char cur = prefix.charAt(i);
              if(t.children[cur - 'a'] == null)return 0;
              t = t.children[cur - 'a'];
          }
          return sum(t);
      }
      public int sum(TrimTree t){
          int sum = t.val;
          for(int i = 0;i < 26;i++){
              if(t.children[i]!=null)
                  sum += sum(t.children[i]);
          }
          return sum;
      }
  
      class TrimTree{
          int val;
          TrimTree[] children;
          public TrimTree(){
              children = new TrimTree[26];
          }
      }
  }
  

• 分析

  1. 前缀树保存所有的key，在每个key的结尾的字符出 记录val
  2. insert操作就是在维护这颗前缀树
  3. sum操作就是先通过前缀树 找到prefix 前缀路径，之后再利用递归遍历当前剩余的树枝，也就是能够满足前缀是prefix的字符串。将val累计 就是结果。

• 提交结果

678. 有效的括号字符串

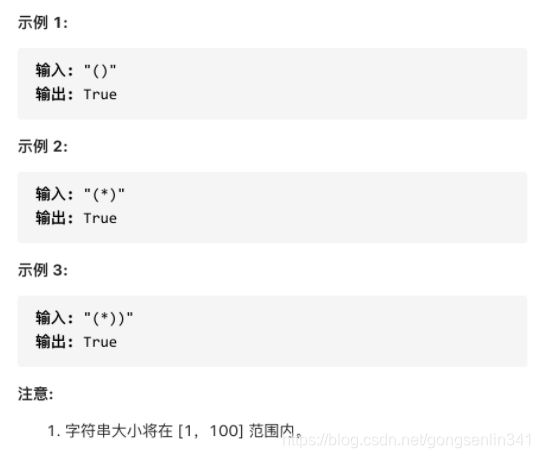
给定一个只包含三种字符的字符串：（ ，） 和 *，写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则：

1. 任何左括号 ( 必须有相应的右括号 )。
2. 任何右括号 ) 必须有相应的左括号 ( 。
3. 左括号 ( 必须在对应的右括号之前 )。
4. 可以被视为单个右括号 ) ，或单个左括号 ( ，或一个空字符串。
5. 一个空字符串也被视为有效字符串。

• 解答

  //方法1
  public boolean checkValidString(String s) {
          return checkValidString(s,0,0,0);
      }
  
      public boolean checkValidString(String s,int leftNumber,int rightNumber,int index){
          if(index == s.length() && leftNumber == rightNumber)return true;
          else if(index == s.length())return false;
          char cur = s.charAt(index);
          if(cur == '('){
              return checkValidString(s,leftNumber+1,rightNumber,index+1);
          }else if(cur == ')'){
              if(leftNumber > rightNumber)
                  return checkValidString(s,leftNumber,rightNumber + 1,index + 1);
              else return false;
          }else{
              if(leftNumber > rightNumber)
                  return checkValidString(s,leftNumber + 1,rightNumber, index + 1) 
              || checkValidString(s,leftNumber,rightNumber + 1, index + 1)
              || checkValidString(s,leftNumber,rightNumber,index + 1);
              else return checkValidString(s,leftNumber + 1,rightNumber, index + 1) 
              || checkValidString(s,leftNumber,rightNumber,index + 1);
          }
      }
  //方法2
  public boolean checkValidString(String s) {
          int n = s.length();
          int min = 0,max = 0;
          for(int i = 0;i < n;i++){
              char cur = s.charAt(i);
              if(cur == '('){
                  min++;
                  max++;
              }else if(cur == ')'){
                  if(max <= 0)return false;
                  if(min > 0)min--;
                  max--;
              }else{
                  if(min > 0)min--;
                  max++;
              }
          }
          return min == 0;
      }
  //方法3
  public boolean checkValidString(String s) {
          int n = s.length();
          Stack<Integer> left = new Stack<>(),star = new Stack<>();
          for(int i = 0;i < n;i++){
              char cur = s.charAt(i);
              if(cur == '(')
                  left.push(i);
              else if(cur == '*')
                  star.push(i);
              else {
                  if(left.size() > 0)left.pop();
                  else if(star.size() > 0)star.pop();
                  else return false;
              }
          }
          while(!left.isEmpty() && !star.isEmpty()){
              if(left.pop() > star.pop())return false;
          }
          return left.isEmpty();
      }
  

• 分析

  1. 方法1 暴力递归
  2. 统计左右括号的数量，当遇到左括号，左括号数量加1，递归遍历下一个位置
  3. 当遇到右括号，如果此时的左括号大于右括号数量，右括号数量加1，递归判断下一个位置
  4. 否则 直接返回false
  5. 当遇到* 号
  6. 如果左括号数量大于右括号数量，那么* 可以代表三种情况，只要其中1种返回true 则是true
  7. 否则* 只能代表 左括号或者 空格两种情况，其中一种返回true 则为true
  8. 递归出口，当index == s.length() 并且 左右括号数量相等返回true，若不相等 返回false
  9. 方法2 贪心
  10. 其实只需要关心左括号数量，最后会不会减少到0即可，因为有*号的存在，所以左括号的数量不确定，可以用至少min和至多max来表示左括号的数量。
  11. 遍历字符串，若遇到左括号，那么min和max都加1。
  12. 如果遇到右括号，如果此时左括号至多max小于等于0 那么说明左括号不够了，返回false，否则max–
  13. 如果此时min大于0，那么抵消掉一个左括号 min–；
  14. 如果遇到*，此时的min如果大于0，那么 * 号可以表示右括号 min–
  15. max至多 也就是 * 表示左括号 max++
  16. 最后返回min是否等于0即可
  17. 方法3 双栈
  18. 一个栈存左括号的索引，另一个栈存*号的索引
  19. 遍历字符串，遇到左括号，左括号索引入栈，遇到*号，入栈
  20. 遇到右括号，优先左括号出栈，如果左括号没有，那么*号出栈
  21. 如果都没有 那么返回false
  22. 遍历结束后，左括号和*号同时出栈，判断索引的大小，如果左括号的索引大于星号的索引 那么表示 后面没有右括号可以匹配了 返回false
  23. 最后如果左括号不为空 返回false 为空 返回true

• 提交结果

  方法1

  方法2

  方法3

679. 24 点游戏

你有 4 张写有 1 到 9 数字的牌。你需要判断是否能通过 *，/，+，-，(，) 的运算得到 24。

• 解答

  static final int TARGET = 24;
      static final double EPSILON = 1e-6;
      static final int ADD = 0, MULTIPLY = 1, SUBTRACT = 2, DIVIDE = 3;
  
      public boolean judgePoint24(int[] nums) {
          List<Double> list = new ArrayList<Double>();
          for (int num : nums) {
              list.add((double) num);
          }
          return solve(list);
      }
  
      public boolean solve(List<Double> list) {
          if (list.size() == 0) {
              return false;
          }
          if (list.size() == 1) {
              return Math.abs(list.get(0) - TARGET) < EPSILON;
          }
          int size = list.size();
          for (int i = 0; i < size; i++) {
              for (int j = 0; j < size; j++) {
                  if (i != j) {
                      List<Double> list2 = new ArrayList<Double>();
                      for (int k = 0; k < size; k++) {
                          if (k != i && k != j) {
                              list2.add(list.get(k));//没有被选到的数字放在list2当中
                          }
                      }
                      for (int k = 0; k < 4; k++) {//枚举4种运算
                          if (k < 2 && i > j) {// + 和 * 的情况下 i < j 的时候已经算过了 i > j的话 就不用重复计算
                              continue;
                          }
                          if (k == ADD) {
                              list2.add(list.get(i) + list.get(j));
                          } else if (k == MULTIPLY) {
                              list2.add(list.get(i) * list.get(j));
                          } else if (k == SUBTRACT) {
                              list2.add(list.get(i) - list.get(j));
                          } else if (k == DIVIDE) {
                              if (Math.abs(list.get(j)) < EPSILON) {//0无法作为除数
                                  continue;
                              } else {
                                  list2.add(list.get(i) / list.get(j));
                              }
                          }
                          if (solve(list2)) {//递归
                              return true;
                          }
                          list2.remove(list2.size() - 1);//回溯
                      }
                  }
              }
          }
          return false;
      }
  

• 分析

  1. 递归回溯
  2. 每次递归 从当前所有的数字当中选择两个数字，然后再选择4个运算中的一种得到的结果 加入到待选择数字当中。当最后只剩下一个数字 并且该数字是24 那么就返回true

• 提交结果

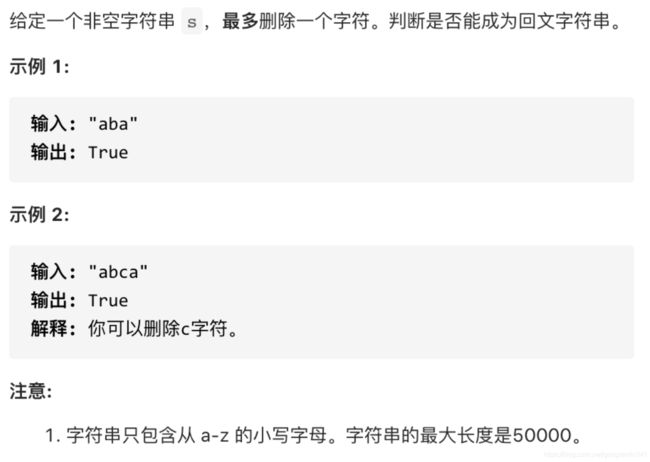
680. 验证回文字符串 Ⅱ

• 解答

  public boolean validPalindrome(String s) {
          char[] chars = s.toCharArray();
          int left = 0;
          int right = chars.length-1;
          while(left < right){
              if(chars[left] == chars[right]){
                  left++;
                  right--;
              }else{
                  return validPalindrome(chars,left+1,right) || validPalindrome(chars,left,right-1);
              }
          }
          return true;
      }
      public boolean validPalindrome(char[] chars,int left,int right){
              while(left < right){
                  if(chars[left] == chars[right]){
                      left++;
                      right--;
                  }else return false;
              }
              return true;
          }
  

• 分析

  1. 双指针，相同 同时移动
  2. 不相同 移动其中一个，判断 两种移动的结果

• 提交结果