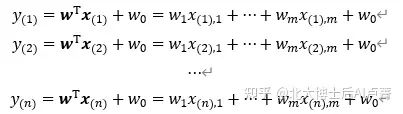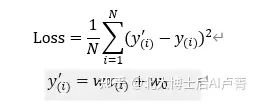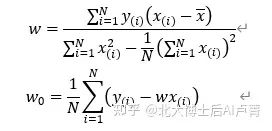《速通机器学习》- 线性回归

（由于平台稿件格式问题，公式格式不能正确写上；如若读写困难可后台私信我要完整电子版）

在企业中，技术人员会将商品的价格、品牌等作为输入来预测商品的销量，甚至通过上市公司的财报、行业信息等来预测公司股票价格的变化。它们的共同点是通过输入来预测输出。在机器学习中，这类业务有一个专门的名字——回归（Regression）。

回归是指通过大量已知数据发现输入 x 和输出 y 的内在关系，并对新的输入进行预测。发现内在关系后，就可以通过它来预测新的输入 x 所对应的输出 y^'。在本章中，我们用 y 表示真实的输出，用 y^' 表示预测的输出。

在使用回归前，需要假设 y^' 和 x 之间的关系类型。这种关系类型称为模型。例如，在 y^'=wx+w_0 中，y^' 和 x 成线性关系（x 的变化按比例影响 y^'），因此该模型也称为线性回归。需要注意的是，y 和 x 之间的关系未必满足我们的假设，它甚至是未知的。

以上只对 y^' 和 x 之间的关系进行了假设，而 w 和 w_0 的值是未知的，因此，需要通过一些方法求解 w 和 w_0。

要想求解 w 和 w_0，首先需要 x 和 y 的一些过往真实数据，例如 (x=3,y=4)、(x=1,y=2.5) 等。这些数据称为训练数据。通过训练数据求解未知的 w 和 w_0 的过程称为学习。学习过程通常是由机器自动进行的，这也是“机器学习”这个词的由来。总之，模型选择是一项人工假设工作，而求解 w 和 w_0 是一个自动定量过程。

当模型训练完毕，w 和 w_0 将对应于已知的数值，例如

y^'=3.2x+1.1

有一个新的输入（可以是从未在训练数据中出现的），就可以计算相应的 y^'，这个过程称为预测。

在使用回归时，y^' 和 x 之间的对应关系不仅可以假设成 y^'=wx+w_0 这种简单的线性形式，也可以由诸如 y^'=w_1 x^2+w_2 x+w_0 这种复杂的形式来表示。形式越复杂，模型蕴含的 x 和 y^' 之间的关系就越复杂，捕捉 x 和 y 之间的关系的能力就越强。但是，复杂的模型会带来一些负面效应，本书后续会进行系统的论述。

2.1　线性回归的基本概念

当输入为1维数据时，线性回归模型如下式所示。

y^'=wx+w_0

显然，此时线性回归在平面上对应于一条直线，这也是“线性回归”名称的由来。

线性回归模型在平面上对应的直线，如图2-1所示。

图2-1

w_0 也称作偏置项。尽管它和输入并无直接关系，但它有重要的作用。如果没有 w_0，那么直线 y^'=wx 必须经过原点，而这极大地限制了模型的能力。

更为一般的情况是，线性回归模型往往是多输入（m 个输入）的。此时，线性回归可以由下式表示。

y^'=w_1 x_1+w_2 x_2+⋯+w_m x_m+w_0

为了简化书写，上式通常可以表示成矩阵相乘的形式。

y^'=w^T x+w_0

其中

有了线性回归模型 y^'=w^T x+w_0，就可以利用训练数据计算模型中的未知参数 w=[w_1,⋯,w_m ]^T 和 w_0 了。

已知数据 〖{x_((i)),y_((i))}〗_(i=1)^N（训练样本）是客观事实。样本数据 x_((i)),y_((i)) 都是成对出现的，

角标 (i) 表示第 i 个训练样本。训练样本一般是通过收集已经发生的事件数据得到的，例如人工标注数据、互联网公司产生的大量日志。

如果输入 x 可以通过运算得到 y^'=w^T x+w_0，那么 y^' 和真实的 y 越接近，w 和 w_0 就越合理，也就是我们越想要的。

有些读者可能会问：是否能够通过解方程的方法求解 w 和 w_0 呢？在这里，我们简单讨论一下。例如，通过已知数据，可以得到如下方程组。

在这里，w_0,w_1,⋯,w_m 为未知数。从数学的角度看，这是一个典型的多元一次方程组。多元一次方程组的求解比较简单，本书不再赘述。然而，在机器学习场景中，解方程本身会遇到以下问题。

训练样本量通常很大（例如，互联网公司的日志数据量往往都以GB为单位计），这意味着可能有海量的方程。这些方程之间往往存在矛盾，很难协调。而如果采用矩阵的形式求解方程，则涉及百万维的矩阵运算，这对算力、机器配置等提出了巨大的挑战，中小型公司通常无法承担。

在线性回归中，因为对应的是多元一次方程，所以方程尚有解析解。但是，模型远不止线性回归一种，当模型非常复杂时，例如

y^'=1/(1+e^(〖-(w〗^T x+w_0)) )

就很难找到有效的解析解了。即使有了解析解，也需要“特事特办”，为每种模型设计一套特有的方法，而这对机器学习的大规模普及和应用是不利的。

在互联网公司中，数据量往往非常大。例如，以过去半年的日志作为训练样本是非常困难的（因为如此规模的数据很难被一次性加载到机器中）。但是，在解方程时需要加载全部数据，这对实操性提出了不小的挑战。

综合上述三个原因，在机器学习领域，很少会采用解方程的方法求解模型的未知参数。为了顺利求解模型参数 w 和 w_0，梯度下降法诞生了。

2.2　损失函数和梯度下降法

首先，让训练数据图形化。当 x 是1维数据时，{x,y} 为二维坐标系中的一个点。训练样本在该坐标系中对应于若干散点，每个点都代表一个样本，如图2-2所示。

图2-2

线性回归希望找到一条合适的直线来尽量多地穿过坐标系中的点，从而使模型和数据尽可能契合。直线由参数 w 和 w_0 决定，不同的参数对应于不同的直线。那么，该如何调整 w 和 w_0 呢？

在实际工程中，每个数据点都具有一定的随机干扰和自身特例，所以大量数据点很难恰巧落在一条直线上（往往散落在直线附近）。因此，无论参数 w 和 w_0 如何取值，都会产生偏离直线的误差。模型学习的目的就是找出一条合适的直线，使各个数据点上的误差之和尽可能小（理想状况为0，但在实际应用中几乎不可能达到）。显然，误差是一个不小于0的数。误差可以表示为下式。

其中，y_((i))^' 表示模型在 x_((i)) 的输出，y_((i)) 表示真实的输出。在这里选择均方误差（Mean Square

Error，MSE）函数作为损失函数，平方计算保证了误差不小于0。需要注意的是，损失函数的类型很多，MSE只是其中之一。

相信细心的读者能看出来，Loss 计算就是求所有数据的预测值 y_((i))^' 和真实值 y_((i)) 之间的

欧氏距离（只是少了开根号的过程）的平均值。

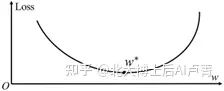
如果 w_0 不变，那么 w 和 Loss 是一一对应关系，即一个 w 值对应于唯一的 Loss 值。投影到二维坐标系，横轴为 w，纵轴为 Loss。如图2-3所示，这是一条典型的抛物线（对应于高维空间中的抛物面）。

图2-3

此时，问题变为找到一个使 Loss 最小的 w。在图2-3中，点 w^* 为 w 的理想位置，即

可以证明 Loss 为凸函数，其存在唯一极小值且极小值为最小值。因此，最小值（极小值）所对应的 w 满足下式。

▒〖〗∂Loss/∂w=2/N∑(i=1)N▒〖(wx((i))+w0−y((i)))〗x((i))=0

同理，最小值（极小值）所对应的 w_0 满足下式。

▒〖〗∂Loss/(∂w0)=2/N∑(i=1)N▒〖(wx((i))+w0−y((i)))〗=0

综合以上二式求解，可得

其中

▒¯x=1/N∑(i=1)N▒x((i))

尽管通过上述方法可以求出最优的 w 和 w_0，但仍存在以下问题。

在训练样本量和特征维度较大时，计算性能和机器内存会成为瓶颈。

上述方法不是通用的。如果 y 和 x 之间的关系比较复杂，并不是简单的线性关系，那么方程可能不存在解析解。

因此，我们需要寻找其他具备通用性的方法，以便应用在大多数机器学习场景中。

在高等数学中，导数可用于衡量函数和变量之间的关系。以输入1维数据为例，模型为 y=wx+w_0，很容易就能得出 Loss 对 w 求导的形式，如下式所示。

▒〖〗∂Loss/∂w=1/N∑(i=1)N▒〖2x((i))(wx((i))+w0−y((i)))〗

∂Loss/∂w>0，表示 w 的变化方向与 Loss 相同。当 w 变大时，Loss 就变大；当 w 变小时，

Loss 就变小。我们的目的是使 Loss 变小。在这种情况下，如果 w 变小，就可以得到一个更

小的 Loss，即变化方向为 -∂Loss/∂w。

∂Loss/∂w<0，表示 w 的变化方向与 Loss 相反。当 w 变大时，可以得到一个更小的 Loss，

即变化方向仍为 -∂Loss/∂w（因为 ∂Loss/∂w<0，所以 -∂Loss/∂w>0）。

∂Loss/∂w=0，表示 w 的变化不会对 Loss 产生影响。在这种情况下，调整 w 是没有任何效

果的，可以认为 w 学习完毕。

学习步骤如图2-4所示。

图2-4

通过以上分析，我们可以得到一个朴素的结论：如果要得到一个更小的 Loss，就需要先随机初始化 w，再让 w 朝一个特定的方向变化。w 的变化方式如下。

w→w-μ ∂Loss/∂w

同理，w_0 的变化方式如下。

w_0→w_0-μ ∂Loss/(∂w_0 )

其中

∂Loss/(∂w_0 )=1/N ∑_(i=1)^N▒〖2(wx_((i))+w_0-y_((i)))〗

μ 是一个 (0,1) 之间的常数，用于控制 w 的变化幅度，避免因 w 变化过大而造成震荡。μ 对学习过程的具体影响，会在本节的结尾进行详细分析。

通过以上分析可以发现，通过导数 ∂Loss/(∂w_0 ) 和 ∂Loss/∂w 分别不断更新 w_0 和 w，Loss 会变得越

来越小。

上述分析过程也可以推广到多维输入。此时，有线性回归

y_((i))^'=w^T x_((i))+w_0 (i=1,2,⋯,n)

x_((i)) 为输入向量，y_((i))^' 为根据 x_((i)) 得到的估计值，y_i 为第 i 个数据的真实值，w 和 x_((i)) 都是

m 维的列向量。损失函数对参数 w 的导数为

∂Loss/∂w=1/N ∑_(i=1)^N▒〖2(w^T x_((i))+w_0-y_((i)))x_((i)) 〗

显然，∂Loss/∂w 也是一个 m 维的列向量。多元函数在某个点的梯度，就是对每个自变量求偏导

并将结果组成一个向量。

同理，可以求出

∂Loss/(∂w_0 )=1/N ∑_(i=1)^N▒〖2(w^T x_((i))+w_0-y_((i)))〗

综上所述，线性回归参数 w 和 w_0 的学习方法，具体如下。

 随机初始化 w 和 w_0，表示为 w(0) 和 w_0 (0)。此时，迭代次数 t=0。

 求当前点 ∂Loss/∂w 和 ∂Loss/(∂w_0 )，公式如下。

∂Loss/∂w(t) =1/N ∑_(i=1)^N▒〖2(〖w(t)〗^T x_((i) )+w_0 (t)-y_((i) ) ) x_((i) ) 〗

∂Loss/(∂w_0 (t))=1/N ∑_(i=1)^N▒〖2(〖w(t)〗^T x_((i) )+w_0 (t)-y_((i) ) ) 〗

 对 w 和 w_0 进行更新，表示为 w(t+1) 和 w_0 (t+1)，公式如下。

w(t+1)=w(t)-μ ∂Loss/∂w(t)

w_0 (t+1)=w_0 (t)-μ ∂Loss/(∂w_0 (t))

 当 t 等于指定的迭代次数或 Loss 的值足够小时，迭代结束。此时得到的 w(t) 和 w_0 (t) 就是学习完成后的参数 w 和 w_0。如果迭代不满足结束条件（t=t+1），则返回第步，进行下一轮学习。

在这里，∂Loss/∂w 就是梯度。w 通过梯度使 Loss 的值不断减小。因此，上述迭代过程也称为梯度下降法。

值得注意的是，梯度 ∂Loss/(∂w(t)) 仅提供了 w 移动的方向，并未提供其移动的距离。如图2-5

所示，在使用梯度下降法时，如果某个点的 ∂Loss/(∂w(t)) 很大，那么在更新参数时可能会出现 w 的

移动幅度过大的问题——在“谷底”两侧不断振荡——矫枉过正。因此，需要对 w 的变化幅度进行限制。

这就是学习率 μ 的作用——防止梯度过大引发的震荡。但是，μ 也不宜过小，因为过小的 μ 会使学习时间延长，如图2-6所示。

图2-5

图2-6

由此可见，合适的学习率对能否快速学习到理想的 w 有重要的影响。

2.3　训练集和测试集

在机器学习中有两个基础的术语——训练集和测试集，它们分别用于模型的训练阶段和训练后的效果评估阶段。

我们在处理一批数据时，一般将数据随机分成两份，训练集占90%，测试集占10%。从概率的角度看，训练集和测试集的数据是从同一概率分布上独立采样得到的。在使用梯度下降法时，用训练集的数据进行训练，测试集不参与训练。训练完成后，我们通常更关心模型在未观测数据上的效果，所以要使用测试集的数据进行效果评测。这样做的好处是能够检测出模型的真实效果，从而避免在训练集上拟合得非常好、Loss 降得很低，但上线后在真实环境中（大量的输入是训练集中并未出现的）对数据模型的拟合效果比较差的问题。

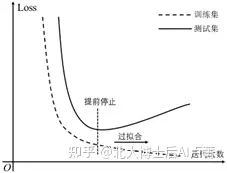
Loss 在训练集和测试集上的差异，如图2-7所示。

图2-7

同一个模型，为什么会在训练集和测试集上效果差异很大呢？我们采集的数据，往往会在一定的规律上添加一些噪声。例如，真实数据由下式产生。

y=4x+3+ε

y=4x+3 是数据产生的规律。ε 为随机噪声，一般符合均值为0的正态分布，即 ε~N(0,σ^2)。噪声通常是由测量误差、一些随机行为或极端特例导致的。噪声这种纯随机事件对机器学习来说是不可学习且不必学习的。

模型在学习时，希望能学到规律，即 y=4x+3，其中并不包含噪声 ε。但是，在训练

样本 〖{x_((i)),y_((i))}〗_(i=1)^N 中，y_((i)) 是包含噪声 ε_((i)) 的（噪声是随机值，可大可小，因此无法剔

除），这就要求模型学习阶段的 Loss 要降低（学会规律），但不能降得过低（把噪声也学会了）。

在训练时 Loss 的值已经降得很低了，但在真实环境中面对大量新数据时仍表现不佳，这种现象称为过拟合（Overfitting），即泛化能力差。产生过拟合的一个原因是模型不仅拟合了规律，还拟合了噪声，另一个原因是真实数据的分布很广，但训练样本过少，无法覆盖全部情况。例如，模型在预测“年龄—消费能力”时，训练样本的数据集中在40岁以下的人群，而在真实场景中出现了50岁以上的人群，必然无法正确进行预测。

解决过拟合问题有多种方法，最直接的方法就是增加训练样本的数量，使模型在训练阶

段实现训练噪声抵消（随机变量 1/N ∑_(i=1)^N▒ε_((i)) 的方差趋近于0，且 N 越大越接近0）。这样，

模型学到噪声的可能性就会大大降低。增加训练样本的数量，也能使模型在学习阶段考虑更多的情况——见多识广。还有一种方法是提前终止学习，只要使 Loss 下降到一定程度即可，无须下降到极小值，以免将噪声拟合进来。

通过以上分析，我们可以得到模型效果的两个评价标准。

降低训练集上的误差，即在训练过程中降低 Loss。

缩小训练误差和测试误差之间的差距。

如果以上第一点没有被满足，那么训练集上的误差将会很大，这就是欠拟合。如果以上第二点没有被满足，就是过拟合。

除了训练集和测试集，还有一个非必需的有效集。有效集是指在训练阶段使用的测试集。例如，有三个学习率 μ_1、μ_2、μ_3，我们并不知道哪一个是最好的。在训练阶段，分别用学习率 μ_1、μ_2、μ_3 做实验，每组实验用相同的训练样本进行模型训练，然后用有效集对这三个模型进行评测，将效果最好的模型作为最终结果。有效集常用于在训练阶段寻找合适的超参数。超参数一般是指梯度无法表达的参数，例如学习率。

打个比方：在准备考试时，训练集相当于平时做的练习题，有效集相当于模拟试卷中的题目（用来找寻最佳学习方法），测试集相当于真实的考试题目。当出现过拟合时，训练集的效果好，测试集的效果差，相当于把训练集中的数据都记住了，但没有真正学到东西，考试时题目稍有变化就抓瞎了。

2.4　多项式回归

在使用模型时，其实隐含了一个潜在要求：模型能力和数据分布相匹配。只有在模型能力和数据分布相匹配时，模型才能得到较好的效果。用机器学习术语来描述，就是归纳偏置（Inductive Bias），即算法对所要学习的问题做出的一些假设。

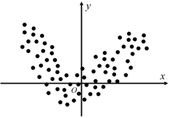
归纳偏置也称为先验（Priors）。在使用线性回归时，默认数据和模型其实是匹配的，即数据尽量在一条直线（在高维空间中对应的是平面）上。但是，如果数据本身不满足模型的归纳偏置，那么在线性回归时数据点将不在一条直线上，如图2-8所示。

图2-8

这时，如果仍然拿线性回归模型去拟合数据，那么无论如何训练，效果都是非常差的。其原因在于，如果模型和数据不匹配，就不可能找出一条直线来很好地拟合抛物线。

我们可以改变模型，使其能尽可能贴近真实数据。例如，可以对线性回归进行扩展，增加一个二次项，使其变为如下抛物线模型。

y^'=w_2 x^2+w_1 x+w_0

这个模型对应的是一条抛物线，该抛物线与数据的分布相吻合，因此可以得到不错的效果。

我们可以从以下两个角度看待这个新模型。

如果把 x^2 和 x 看成两个独立的变量，那么该模型仍然是线性回归，只不过输入有两个维度（x^2 和 x）。

如果把 x 看成一个变量，那么模型就是一个抛物线回归模型（非线性多项式回归模型）。

如果点的分布更加复杂，就可以通过提高拟合函数的阶次来取得更好的效果，例如引入 x^3、x^4 等。阶次越高，函数在训练集上的效果就越好，能够拟合的曲线的种类就越多，模型的复杂度就越高、容量就越大。这里的容量是指模型的潜在能力，即能够拟合的曲线的种类有多少。

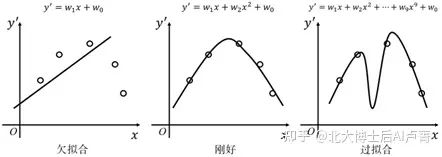
当然，模型的复杂度不能一味提高（避免发生过拟合）。一方面，高阶次函数的引入会带来输入的轻微变化，导致输出迅速增大，引起震荡。另一方面，当函数的阶次过高时，拟合曲线可能会经过训练样本中所有的点，同时把噪声学到了，导致过拟合。例如，使用线性回归拟合一条二次曲线：在只采用一次项时，会发生欠拟合，在训练集上 Loss 的值过大；如果采用二次项，就可以拟合得刚好（这正是我们需要的）；如果继续增加高阶项，如增加到9阶，就会发生严重过的过拟合（尽管曲线会将所有训练数据完美匹配，但曲线已不是二阶抛物线了），在测试集上的效果必然很差。

上述分析，如图2-9所示。

图2-9

因此，不仅在线性回归上，在任何模型的选择上，复杂度和容量的添加一定要适可而止，切忌画蛇添足。

在机器学习领域有一条“金科玉律”，即没有免费午餐定理（No Free Lunch Theorem）。没有免费午餐定理是由Wolpert和Macerday在最优化理论中提出的，它证明了：对基于迭代的最优化算法，不会存在某种算法对所有问题（在有限的搜索空间内）都有效的情况。如果一种算法对某些问题有效，那么它一定在另一些问题上比纯随机搜索算法的效果差。也就是说，任何算法都有自己的优势和劣势，不能脱离具体问题讨论算法的优劣，必须“具体问题具体分析”。没有免费午餐定理告诉我们：没有绝对好的模型，模型在一些问题上“好”的表现一定是以在另一些问题上“坏”的表现为代价的。

在上述例子中：如果数据天然是以线性分布的，那么线性回归的效果就比较好，其代价是在非线性分布的数据上欠拟合；如果数据本身是以多项式分布的，那么阶次合适的多项式回归就能很好地完成任务，其代价是在线性分布和低阶次数据上过拟合。

2.5　线性回归的高级技巧

2.5.1　特征敏感性研究

在一维线性回归中，x 是输入，y^' 是输出，模型为 y^'=wx+w_0。现在，将输入数据增加1维，使其变成 [x_1,x_2 ]^T，x_1 为原来的输入 x，x_2 为符合 N(0,σ^2) 的随机数，模型将变为 y^'=w_1 x_1+w_2 x_2+w_0。例如，我们希望通过模型预测一个人的退休金是多少，x_1 表示他的工龄，x_2 表示他的身高，可以看出，x_2 对预测结果毫无帮助，纯粹是一个随机变量。

通过实验可以发现，当训练的数据量足够大时，经过训练，w_2 将趋近于0。假如原来的学习结果为

y^'=400x+1000

那么维度扩增后的学习结果为

y^'=4〖00x〗_1+0.001x_2+1000

可以看出，x_2 对于曲线的拟合基本没有帮助——这符合我们的认知。这同时说明，线性回归具有对抗噪声的能力，即无关的随机输入不会对模型的效果产生影响。

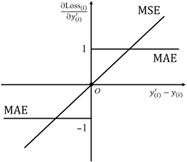
值得注意的是：当样本量较小时，随机特征 x_2 很难相互抵消（这会造成负面影响）。例如，只有A、B两个样本，恰好“A_退休金>B_退休金”“A_身高

换一个角度看，如果某维度特征所对应的 w 在数值上接近0，就可以从侧面反映出该特征不是特别重要，或者和其他特征放在一起时出现了冗余现象，即不同的特征代表了相同的信息，那么，该特征可以被剔除，从而降低运算量。

接下来我们讨论特征冗余现象。假设有一个2维特征，其第二维特征不是随机的，而是通过简单复制第一维特征得到的，即输入特征为 [x_1,x_2 ]^T，x_1 和 x_2 均为原有特征，x_1=x_2。可以看出，虽然增加了1维特征，但没有增加信息量，x_1 和 x_2 仍是相互冗余的。

假如原来的学习结果为

y^'=400x+1000

那么维度扩增后的学习结果为

y^'=ax_1+bx_2+1000

通过实验可以发现，如果满足 a+b=400 这一约束条件，那么 a 和 b 可以是任意值。特别地，如果在训练时使用L2正则（将在3.4节详细介绍），那么 a=b=200。由此可知，如果特征出现了冗余现象，那么权重将会分散到各个冗余维度上。因此，我们不能简单地通过权重来衡量特征的重要性。特征所对应的权重低，虽然可能是该特征不重要造成的，但不能排除其他维度的特征和它形成冗余现象从而造成权重被稀释的情况。

由上面两个例子可知：如果单纯增加噪声，那么在样本量足够时，虽然不会对最终的学习结果产生很大的影响，但会增加运算量；如果样本量不足，那么为特征增加噪声会对模型产生误导。如果发生了特征冗余，那么不仅无法提升最终的学习效果，还会稀释权重。

上面两个例子有哪些应用场景呢？首先需要说明的是，在这两个例子中，冗余现象（完全复制）和噪声（完全随机）的假设过于极端。在真实场景中，除非刻意，这样的情况是不太可能出现的。但是，一定程度的冗余现象和噪声经常会出现。例如，婚介场景使用的特征为月收入、房产（房屋数量和面积）、汽车品牌、天气。月收入、房产、汽车之间存在一定程度的冗余现象，但不是完全冗余的，例如汽车品牌除了和月收入有关，还和个人喜好及品味相关。而天气对相亲成功与否来说是无关因素，因此作为噪声出现。

在企业里做项目，涉及的特征往往会达到上千维甚至更多。大量特征难免相互冗余，或者有些特征因为对任务的帮助不大而被当作噪声。因此，弄清楚冗余现象和噪声这两个问题，对特征提取和模型的可解释性都会有帮助。

2.5.2　损失函数的选择

一般来说，线性回归的损失函数为MSE。MSE用于衡量预测值和真实值之间的差别，并且是恒大于0的。可能有读者会问：是否有其他形式呢？当然有。例如，将MSE换成平均绝对误差（Mean Absolute Error，MAE），损失函数的公式如下。

Loss=1/N ∑_(i=1)^N▒Loss_((i)) =1/N ∑_(i=1)^N▒| y_((i))^'-y_((i)) |

上式也能用来衡量实际值 y_i 和预测值 y_i^' 之间的差异，并能保证值不小于0。但是，在真实场景中，几乎不会将绝对值函数作为损失函数，原因大体如下。

在模型求解时一般采用梯度下降法，这就要求损失函数的导数是存在的，如果导数不

存在，后续的步骤就无从谈起。但是，由于 Loss_((i))=|y_((i))^'-y_((i)) |，在 y_((i))^'=y_((i)) 这个点

导数不存在，因此，使用梯度下降法会遇到障碍。在机器学习中，对于导数不存在的点，一般可以根据经验为其设置一个导数，从而在一定程度上解决这个问题。

然而，更麻烦的是下面这一点。

当 y_((i))^'≠y_((i))，Loss 分别为MSE和MAE时，(∂Loss_((i)))/(∂y_((i))^' ) 的函数图像如图2-10所示。可以发现，在将MSE作为损失函数时，对距离目标点 y_((i)) 较远的数据点的导数 〖∂Loss〗_((i))/(∂y_((i))^' ) 较大，所以更新幅度 〖∂Loss〗_((i))/∂w=〖∂Loss〗_((i))/(∂y_((i))^' ) 〖∂y〗_((i))/∂w 较大。而在将MAE作为损失函数时，无论误差是多少，更新“力度”都是一致的，即 〖∂Loss〗_((i))/(∂y_((i))^' )=1 或 〖∂Loss〗_((i))/(∂y_((i))^' )=-1。因此，MSE更智能，更看重误差较大的数据点。

图2-10

我们还可以从最大似然估计的角度来论证将MSE作为损失函数的合理性。正如前面分析的，假设数据的产生过程如下。

y_((i))=w^T x_((i))+w_0+ε

在上式中，ε 为随机变量，满足0均值正态分布，即

P(ε=e)=1/(σ√2π) exp^(-e^2/(2σ^2 ))

因此，y_((i)) 也是一个随机变量，符合正态分布，即当 x_((i)) 已知时，满足

P(y=y_((i)) |x_((i)) )=1/(σ√2π) exp^(-〖(y_((i) )-w^T x_((i) )-w_0)〗^2/(2σ^2 ))

机器学习的目标是从数据中找到最优的 w 和 w_0。量化最优除了可以让预测的 y^' 和真

实的 y 的差别最小，还可以从统计学的角度，通过调整参数使训练样本 〖{x_((i)),y_((i))}〗_(i=1)^N 出现

的概率最大，即使真实的 y 所对应的似然函数最大。因此，对于所有训练样本，似然函数为

likehood=∏_(i=1)^N▒〖P(y=y_((i) ) |x_((i) ) )=∏_(i=1)^N▒〖1/(σ√2π) exp^(-〖(y_((i) )-w^T x_((i) )-w_0)〗^2/(2σ^2 )) 〗〗

为了运算方便，我们对似然函数取对数，使似然函数变为

likehood=log⁡[∏_(i=1)^N▒〖1/(σ√2π) e^(-〖(y_((i) )-w^T x_((i) )-w_0)〗^2/(2σ^2 )) 〗]=∑_(i=1)^N▒[-〖(y_((i) )-w^T x_((i) )-w_0)〗^2/(2σ^2 )-logσ√2π]

模型学习的目标就是最大化似然函数 likehood，即已经发生的事实，因此，其对应的概率应该最大。

max⁡(likehood) 即最小化 min⁡(-likehood)，因此，优化目标为最小化下式。

∑_(i=1)^N▒[〖(y_((i) )-w^T x_((i) )-w_0)〗^2/(2σ^2 )+logσ√2π]

由于在似然函数中，只有 w 和 w_0 为变量是我们希望求解的，其他无关项均可去除，所以，优化目标变为最小化下式。

∑_(i=1)^N▒〖〖(y_((i) )-w^T x_((i) )-w_0)〗^2=∑_(i=1)^N▒〖(y_((i) )-y_((i))^')〗^2 〗

可以发现，上式就是前面所讲的MSE。可见，当数据符合正态分布时，使用MSE优化线性回归模型等价于最大似然估计。

---

对机器学习感兴趣的读者可以去主页关注我；本人著有《速通深度学习》以及《速通机器学习数学基础》二书，想要完整版电子档可以后台私信我；想一起学习机器学习的话也可以后台私信，本人所做机器学习0基础教程已有60余章还未公开；想了解的话也是后台私信或者评论区留言。