密码学理论07:密码哈希函数
哈希函数 H : {0, 1}^∗ → {0, 1}^n 将长字符串映射到短“摘要”,不同的上下文有不同的概念。
- 非密码学的:最初为数据结构(哈希链表)发明的通用/k-wise 独立哈希函数。用于信息论加密(一次性 MAC)或作为加密方案的构建块(hash然后加密/Carter-Wegman MAC)。【目标:尽可能减少碰撞但不追求抗碰撞】
- 密码学的:哈希函数(抗冲突性、单向性等)广泛用于密码学应用程序(例如数字指纹、区块链、哈希然后验证)。【目标:抗碰撞】
- 理想的:哈希函数,又名 “随机预言模型”,其中 H 被建模为随机函数,在标准假设不充分时用于密码安全证明。
抗碰撞性
非正式地,如果 PPT 算法无法找到冲突,即 x≠ x′ s.t. H(x)=H(x ′ )。则 H : {0, 1}^∗ → {0, 1}^n(或 H : {0, 1}^m → {0, 1}^n , m ≥ n)是抗冲突的。
碰撞始终存在(因为 m > n),这个直观的概念是无法实现的。
实用解决方案:可以使用可以破坏原语的算法来查找 H 的碰撞,并且据信这对于像 SHA256 这样的特定结构来说很难。
理论解决方案:考虑一系列哈希函数,一定很难从这个族中找到任意随机哈希函数的碰撞。
【定长哈希函数/压缩函数】
【抗碰撞性】
较弱的安全概念
- 抗第二原像攻击或抗目标碰撞:
给定 s 和随机 x,很难找到 x ′ ≠ x s.t. H(s, x) = H(s, x ′ )。
-
原像抵抗或单向性:给定 s 和 y,其中 y:= H(s, x) 。对于随机 x,很难找到 x′(不一定 x′≠x)s.t. H(s, x′ ) = y。
与抗碰撞不同,1.和 2. 对固定 H(·) 有意义,即没有s;抗碰撞性隐含1.& 2.。满足 1. 或 2. 的函数可以从任何单向函数构造。
CRHFs的域扩展
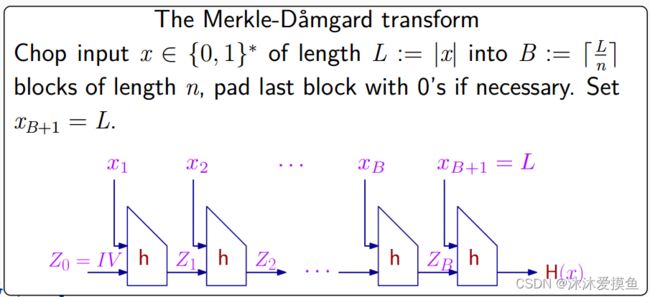
在实践中,散列函数是通过首先设计一个压缩函数来构造的,比如 h : {0, 1}^2n → {0, 1}^n ,然后使用 h 的操作模式进行域扩展,最终得到一个 H : {0, 1}^∗ → {0, 1}^n,对于无限长度输入。
MD变换:
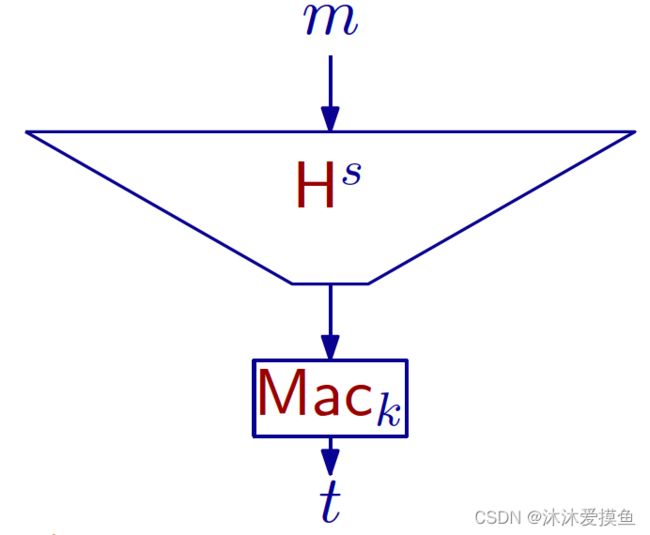
Hash-and-MAC
如果 Π 是长度为 ℓ 的消息的安全 MAC,并且 H 是抗冲突性的,则 Π ′ 是安全 MAC(对于任意长度的消息)。
使用hash函数作为 MAC
使用加密散列函数的临时构造曾经(现在?)大量用于身份验证,因为:
- 有可用的哈希函数的快速实现。
- 通常由对加密不太了解的人完成实施。
HMAC
(嵌套 MAC)NMACk1,k2 (m) = H(k2||H(k1, m)) 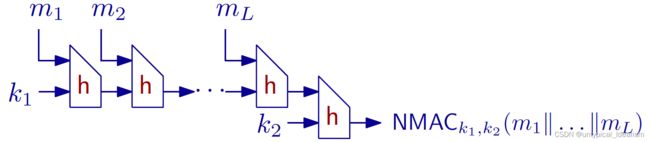
如果 h(·,·) 是 PRF(第一个输入是密钥),则 NMAC 是 PRF(因此是 MAC)。
HMACk(m) = H(k ⊕ opad||H(k ⊕ ipad||m))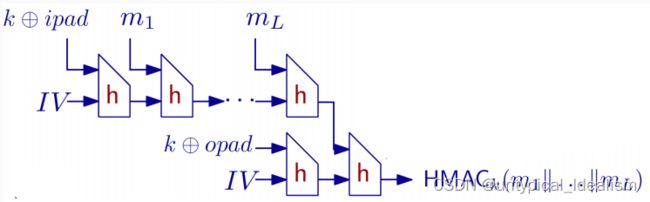
HMAC 是实践中使用的 NMAC 的更实用的变体:
- 通过对固定的 ipad、opad 进行异或运算,从单个密钥 k 派生密钥。
- 假定级联固定 IV
- 除了作为 PRF 之外,安全性证明还需要对 h 做一些额外的假设。(抗碰撞性)
对hash函数的通用攻击
在 q 不同的 x1, ..., xq 上查询 H(·)时
鸽笼原理:如果 q = 2 ℓ + 1 则 ∃i ≠ j s.t. H(xi) = H(xj);
生日悖论:如果 q 个元素 y1, ..., yq 从大小为 N 的集合中独立均匀地随机采样,则: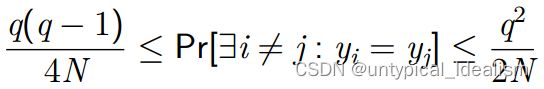
——必要不充分条件:ℓ > 2log(q)
哈希函数的应用
随机预言机模型
有部分基于加密哈希函数的构造示例,仅基于哈希函数具有抗冲突或原像抗性的假设无法证明其安全。
随机预言机模型是 一种在实践中取得成功的方法,它在完全严格的安全证明和没有任何证明之间提供了一个“中间地带”:引入一个理想化的模型来证明密码方案的安全性。
- 假设随机函数 H: {0, 1} ∗ → {0, 1} n 存在于“天上”,可以被所有人查询。
- 在安全实验开始之前采样的“fresh”H。
随机预言机方法:
- 在 RO 中设计并证明方案的安全性。
- 在现实世界中,RO 是用加密哈希函数实例化的。( H 实现了一个伪随机生成器)
这是一种启发式,而不是证明。表明方案结构没有固有的设计缺陷。
总比没有证据好,而且在实践中出人意料地可靠。
数字指纹和重复数据删除
病毒指纹识别:病毒扫描程序仅存储计算机病毒的哈希值。足以识别它们。为了避免被发现,计算机病毒可以“变异”。
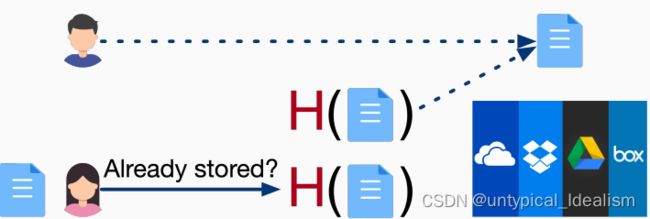
重复数据删除:云存储提供商将所有存储文件的哈希值保存在一个小型数据库中。如果用户要上传新文件 x,将检查服务器是否存储了 H(x):
- 如果是,文件已经存在,不需要上传,只存储一个指针。节省带宽和存储空间。
- -如果 H 是抗冲突的,恶意客户端就不能使服务器返回错误的文件。
Merkle Tree
——防篡改(验证文件完整性)
如果客户端存储了很多文件 F1, F2, ..., Fℓ 他可以存储所有 hi := H(Fi)。——线性的空间复杂度
在本地只存储一个散列 ϕ = H(h1, ..., hℓ)。——检索所有 h1, ..., hℓ 需要线性通信复杂度。
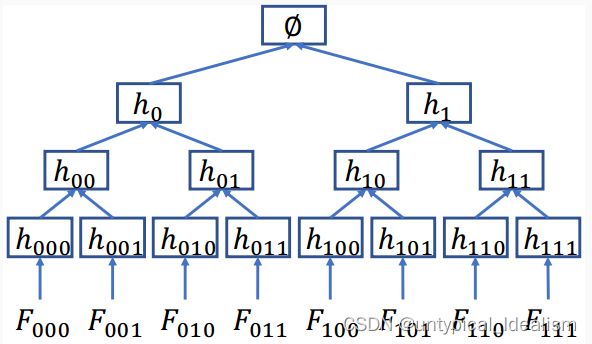
MTt (F1, ..., Ft) = ϕ 其中 hx = H(Fx),hx = H(hx||0, hx||1),根 ϕ = H(h0, h1)。
定理:如果 (Gen, H) 是抗碰撞的,那么 (Gen, MTt ) 也是抗碰撞的(对于固定的 t)。
客户端存储 ϕ,服务器存储 Fi 和所有 h。
如果客户端请求文件,比如 F010,服务器会发送 F010 以及计算根所需的所有 log(ℓ) h 值【F011、h011、h00、h1】。如果重新计算的根值仍是 ϕ,它会接受。
基本密码协议
pwd:有限的密码集
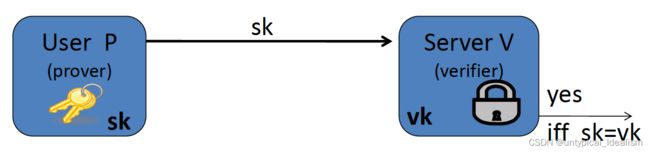
算法 G (KeyGen): 选择 pw ← PWD。输出sk=vk=pw。
问题:vk 必须保密。
——服务器的妥协会暴露所有密码!
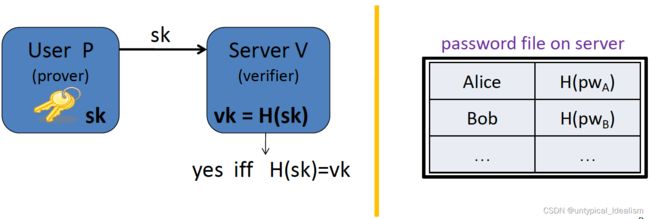
H:从 PWD 到 X 的单向哈希函数
问题:弱密码选择(用户经常选择弱密码)——口令猜测攻击。
在线字典攻击:攻击者有一个用户名列表。对于每个用户名,攻击者都会尝试密码“123456”——平均 33 次尝试后成功。
离线字典攻击:假设攻击者从服务器获得单个 vk = H(pw)。hash字典中的所有单词,直到找到满足 H(w) = vk 的单词 w。
时间复杂度:每个密码 O(|Dict|)。
批量离线字典攻击:假设攻击者窃取了整个 pwd 文件 F,获取所有用户的散列密码。对于每个 w ∈ Dict:测试 H(w) 是否出现在 F 中(使用快速查找)。
时间复杂度:O(|Dict|+|F|)
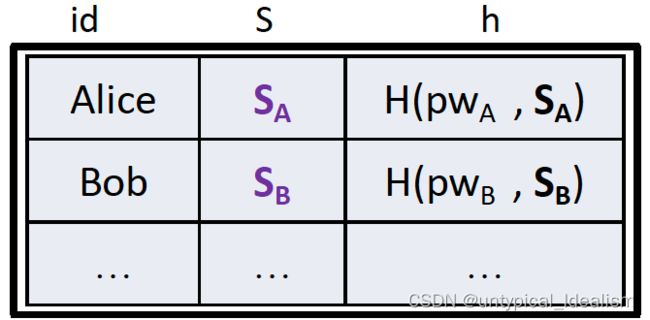
防止批量字典攻击:public salt——设置密码时,随机选择一个n位salt S,当验证A 的pw 时,测试是否H(pw, SA)=hA。
攻击者必须为每个用户重新散列字典。批量攻击时间复杂度:O(|Dict|×|F|)。
缓解离线字典攻击:使用“慢速”散列函数,或通过使用多次迭代来减慢现有散列函数的速度;设置salt;使用服务器辅助方式。