插入排序详解

插入排序详解

​ 摘要：插入排序是一种非常有意思且比较高效的排序方法，同时插入排序是希尔排序的基础，现在我们来看看插入排序。

1.插入排序算法详解

​ 插入排序和选择排序有一个异曲同工的地方在于他们都存在一个：在原数组上创建子数组的思想，这两种排序方法都会将原数组分为两个部分：待排序数组与已排好序的数组，但是这两种算法的内核思想却截然不同，现在我们来理解一下插入排序是怎么实现的。

​ 首先我们得到了一个无序的数组，现在我们将这个数组视为两部分，无序数组，已排好序的数组：

​ 蓝色部分代表未排好序的数组，而绿色部分代表已排好序的数组，这两个数组都位于这个全部的数组之上，当然现在全部数组都是一个无序数组，因此我们看不见绿色，整个数组都是蓝色的，但是我们可以想想：在数组的首元素之前，有一个虽然不存在，但是在概念上存在的有序数组区域，它一直存在，只不过它现在是空的而已，接下来我们要做的，就是从无序数组中取得元素，并插入到这个有序数组中去。

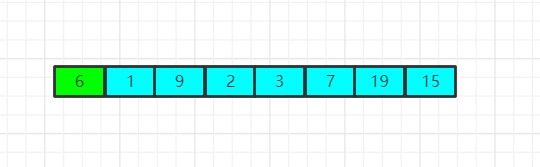
​ 如下图所示，我们拿到了无需数组中的第一个元素：6，并将其插入到有序数组中去，此时有序数组中什么都没有，因此不需要对6这个元素进行任何操作，直接放进去，这个有序数组的有序性没有被改变，其仍是一个有序数组，因为只有一个元素的数组，谈不上有没有顺序概念，我们完全可以将其视为一个有序数组：

​ 现在，有序数组和无序数组的分解开始显现出来了，现在我们继续从无序数组中取值，并放进无序数组中去。不同的是，这次，我们取到的数字是1，我们如果直接将1放进有序数组是不行的，因为直接放进去的话会导致有序数组变为无序数组：

​ 因此我们需要让1进行移动，让它在有序数组中进行移动，直到它移动到合适自己的位置即可，因为我们已知有序数组是有序的，因此对于新加进来的元素1，我们应该让它开始和有序数组中的最后一个元素开始往前进行比较，直到找到了一个比它还小的元素后才停止，这里，1应该移动到6后边：

​ 这样一来有序数组就又变得有序了，之后我们继续将无序数组的元素向有序数组中加，下一个元素是9，我们在经过对比后，发现9是大于当前有序数组的最后一个数字：6的，因此9无需后移：

​ 我们继续将无序数组中的元素往有序数组中放，这次我们取得的元素是2，我们发现2是比当前有序数组的最后一个数组小的，因此要往前移动一次，在移动一次之后，我们发现2仍然比它前一个元素小，因此这时2仍然会使这个有序数组变得无序，因此我们还需要让2进行前移，知道2移动到了1后边，经过对比我们发现2比1大，这时2无需继续移动了，因此此时数组是这样：

​ 我们继续重复上面的行为，发现了下一个要加入有序数组中的数字为3，同样，我们重复上述的对比行为，如果3前边的数字比3大，就要将它往前移动，因此在移动好之后，我们会得到这样的数组：

​ 下一个数字是7，我们现在要将7放入到有序数组中去，7放到有序数组中之后要开始和它前边的元素进行对比，发现当前7前边的数字是9，因此7需要往前移动，移动之后，我们发现7前边的数字是6，这是7大于6，因此不再需要移动了：

​ 我们继续从无序数组中向有序数组中插入元素，发现下一个是19，显然插入19之后，我们发现19大于其前边的元素值：9，因此19不需要进行前移了：

​ 现在我们继续将无序数组中的元素向有序数组中插入，发现此时无序数组中还剩一个：15，因此我们将其插入到有序数组的尾部，这时我们发现15比它前边的数字19小，因此15需要往前移动，在移动之后我们会发现15后边的数字是9，这是15大于9，因此15遍不再需要移动了，而这时无序数组也从原数组空间上消失了，整个数组变成了一个有序数组：

2.算法总结

​ 根据图解，我们现在可以理解插入排序的过程了(以从小到大排序为例)：我们将原数组空间看成两个部分，前边是有序部分，后边是无序部分，有序部分我们默认为它就已经是排好序的，它内部已经是从小到大有序的状态了，即使当前它是空的，它也具备这个特征。然后我们不断的取无序数组的首元素，向有序数组的尾部添加，我们在这里并没有真正的将它取出，并且再添加回来，因为根据我们的定义，有序数组的尾部正好就和无序数组的头部相邻，这只是一个更改标记的事情，我们只要把有序数组的长度加1，无序数组的长度减一，并且将有序数组的头部元素指针指向它的下一个，就可以完全准确的代表这个行为。因此这时我们已经将无序数组的首元素取出，并插入在了有序数组的尾部，然而这时，在尾部新加入的元素有可能会导致整个有序数组变得无序，因此我们需要进行调整。而调整方式就是将新加入的元素进行对比并根据对比结果往前移动，这个移动过程有点像冒泡排序的过程：新加入元素和它前边的元素进行对比，如果它比它前边的元素小，则二者互换位置，重复这个行为，直到它前边的元素小于它才会停止，这样一来，有序数组就仍然是有序数组了。我们重复这个向有序数组中插入不断插入数据，并在插入之后通过操作使其变得有序的行为，在这个过程中我们会一个一个的拿走无序数组中的首节点并一个一个单位的减少无序数组的规模，并一个一个的向有序数组中添加并扩大有序数组的规模，直到最后整个无需数组被掏空，有序数组占据了原数组空间的所有空间时，整个数组排序宣告完成。

3.代码分析

​ 接下来我们来看看插入排序的具体代码：

public static void insertSort(int[] arr){
        for (int i = 1; i<arr.length; i++){//①
            for (int j = i-1; j>=0; j--){//②
                if(arr[j]>arr[j+1]){
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }else
                    break;
            }
        }
        System.out.println(Arrays.toString(arr));
    }

​ ①标记了外部的大循环，这个循环实际上就是驱动有序数组一个一个增加，无序数组一个一个减少的动力，在此，i就代表了无序数组的首节点位置，因为当数组中有一个元素时它必定有序，所以我们在这里可以忽略掉往插入第一个元素的行为，直接从第二个开始插入。

​ ②标记了外部循环中的一个内循环，外循环的每次执行，实际上都代表了我们将无序数组中的首元素拿下来放到有序数组的尾部，而这里这个内循环，实际上就是移动这个新来的元素，使有序数组重新变得有序的机制，我们可以看到，j指向的是i-1，这个位置就是当前有序数组没有插入新元素之前的尾部位置，在这个循环中，j要一直和j+1进行对比，j+1指向的就是新加入的元素，如果j指向的元素大于j+1指向的元素的话，二者就要进行一个类似冒泡排序的互换，将j+1指向的元素和j指向的元素进行互换，在互换之后，j指向了新加入的元素，而j+1则指向了之前新元素前边的元素，也就是之前的数组尾部，这时j自减一次，这就导致j+1又重新指向了新加入的元素，而j也又指向了新加入的元素的前一个元素，新元素得以继续同它前边的元素进行对比，当经过对比发现，新加入的元素已经大于前边的元素之后，说明新加入的元素已经移动到了自己正确的位置，这个移动行为就可以终止了。

​ 插入排序的精髓在于设置一个有序的空数组，从它为空的时候就认定其为有序数组，并在不断的插入新元素的过程中维护其有序性，这样一来，我们实际上一直在干的事情就是向一个有序数组中不断地插入新元素，这比进行直接排序的操作手法会简单的多。以上就是插入排序。