leetcode刷题笔记_二叉树相关
二叉树相关
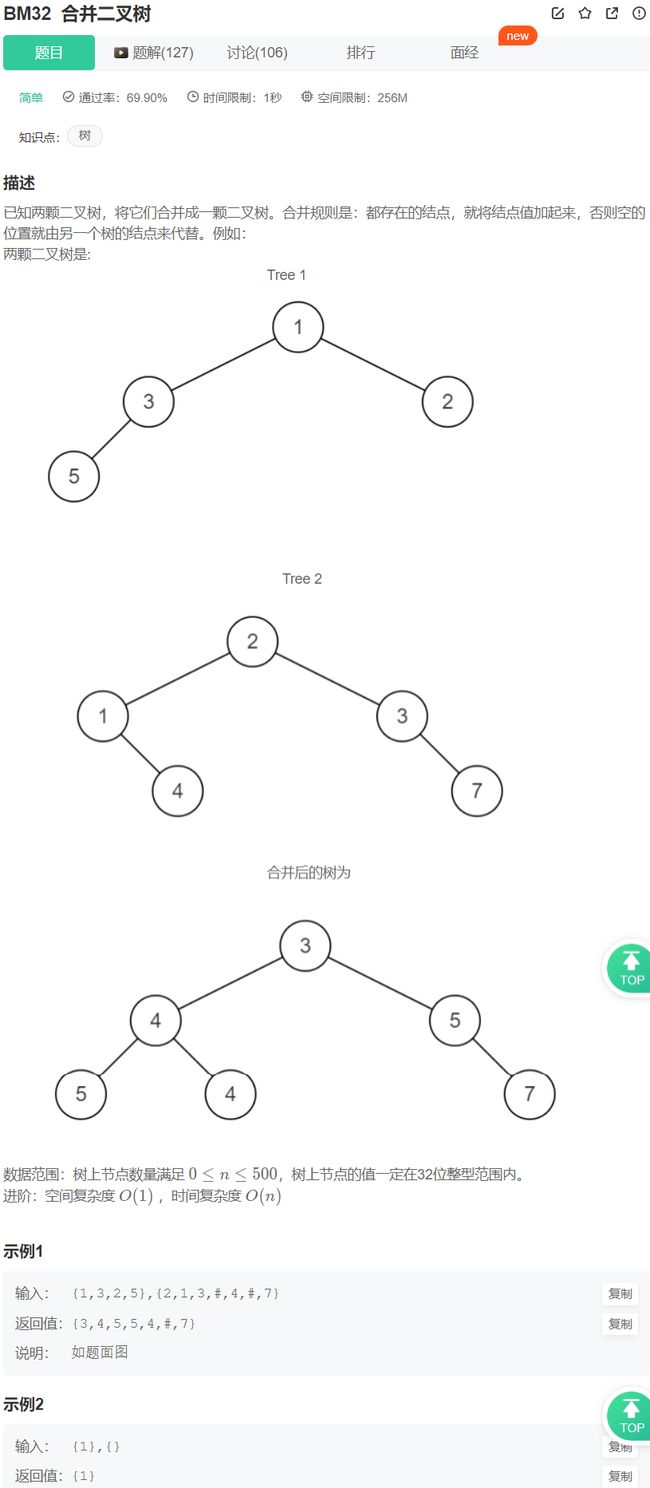
- 合并二叉树:
- 二叉搜索树相关
-
- 第98题 验证二叉搜索树
- 第99题 恢复二叉搜索树
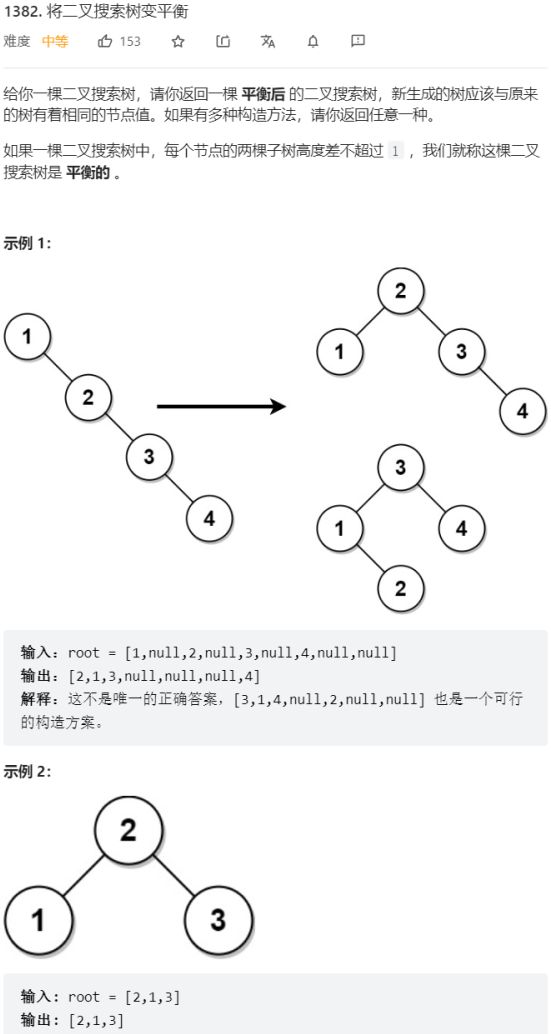
- 第1382题 将二叉搜索树变平衡
-
- 中序遍历+有序数组构建AVL树:
- *通过递归,自下而上不断地旋转,直到二叉搜索树满足平衡树AVL的条件:
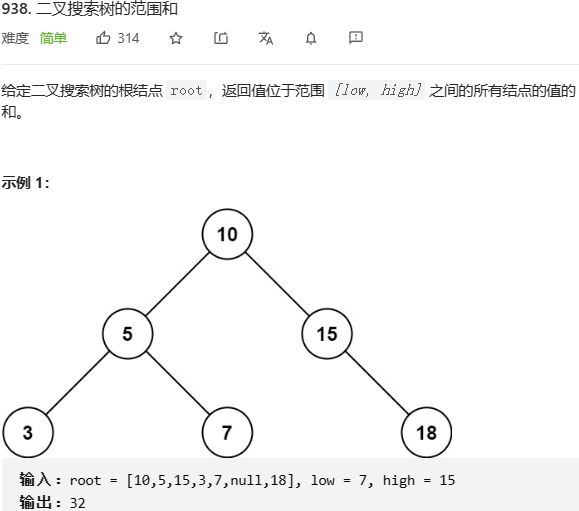
- 第938题 二叉搜索树的范围和
- 第110题 高度平衡的二叉树
-
- 自顶向下递归:
- 自底向上递归:
- 不同的二叉搜索树:
-
- 第96题 不同的二叉搜索树
-
- 动态规划DP:
- *第95题 不同的二叉搜索树II
-
- 递归回溯:
- *第222题 完全二叉树的节点个数
- 树的子结构:
- 与树的遍历有关:
-
- 第199题 二叉树的右视图
-
- 层序遍历+队列:
- 第230题 二叉搜索树中第k小的数
-
- 中序遍历+递归:
- 中序遍历+迭代(无需全树遍历):
- 第144题 二叉树的前序遍历
-
- 递归/DFS:
- 迭代(借助栈):
- 第94题 二叉树的中序遍历
-
- 递归形式:
- _迭代形式:
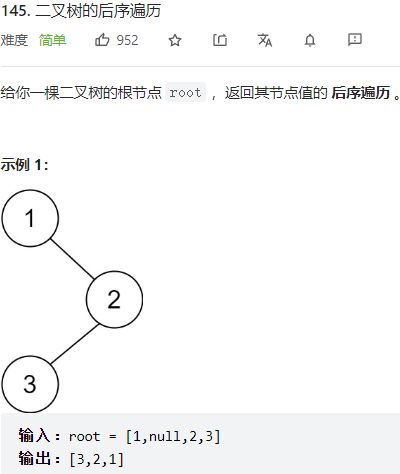
- 第145题 二叉树的后序遍历
-
- 递归/DFS:
- 迭代:
- 后序遍历相关:
-
- 验证二叉搜索树的后序遍历序列
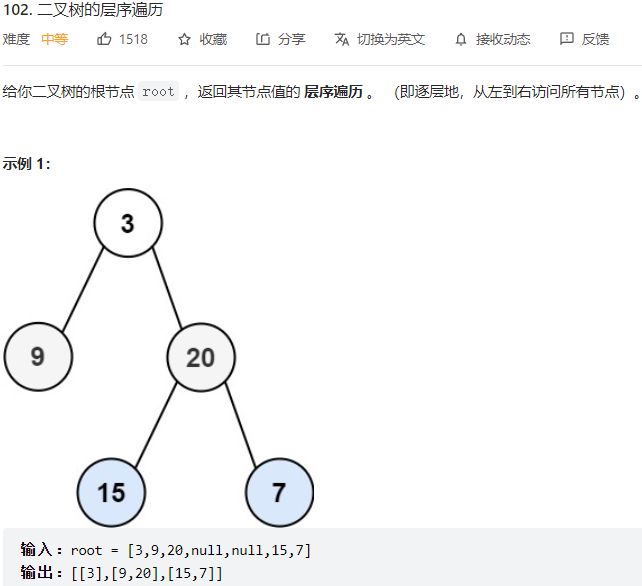
- 第102题 二叉树的层序遍历
-
- 借助队列:
- 层序遍历相关:
-
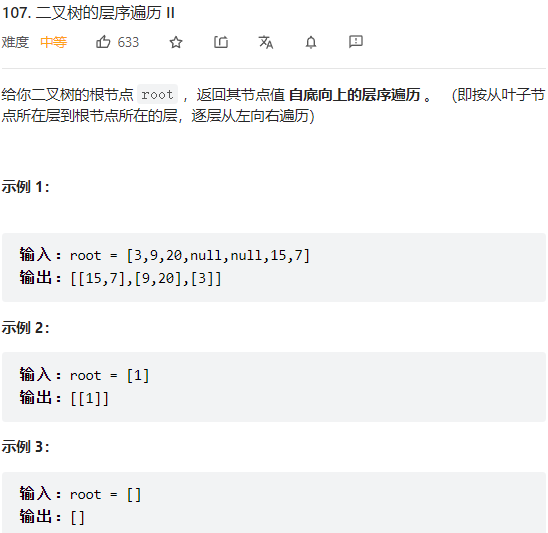
- 第107题 二叉树的层序遍历II
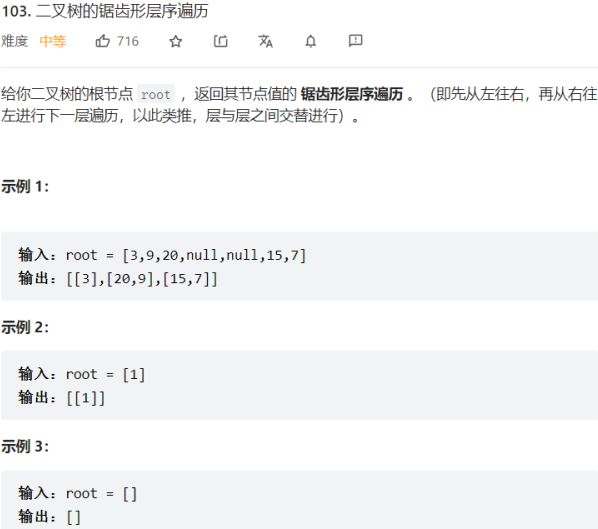
- 第103题 二叉树的锯齿形层序遍历
- 第116题 填充每个节点的下一个右侧结点指针
- 根据遍历结果重建二叉树:
-
- *第105题 从前序与中序遍历序列构造二叉树
- *第106题 从中序与后序遍历序列构造二叉树
- 二叉树路径相关:
-
- 第257题 二叉树的所有路径
- 二叉树的路径和:
-
- 自顶向下:
-
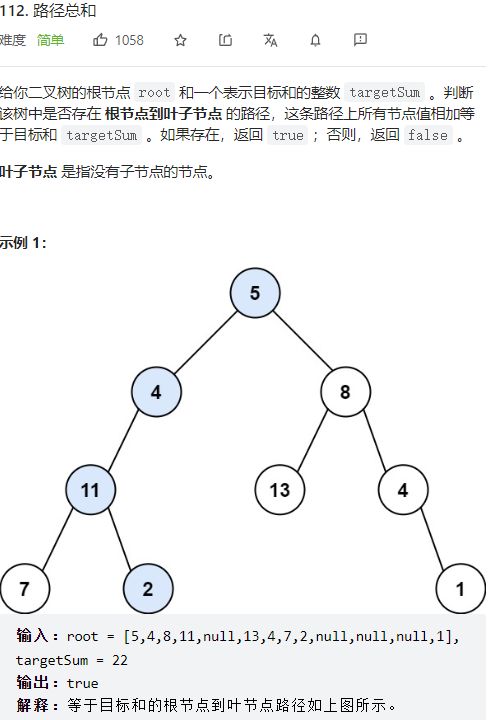
- 第112题 路径总和
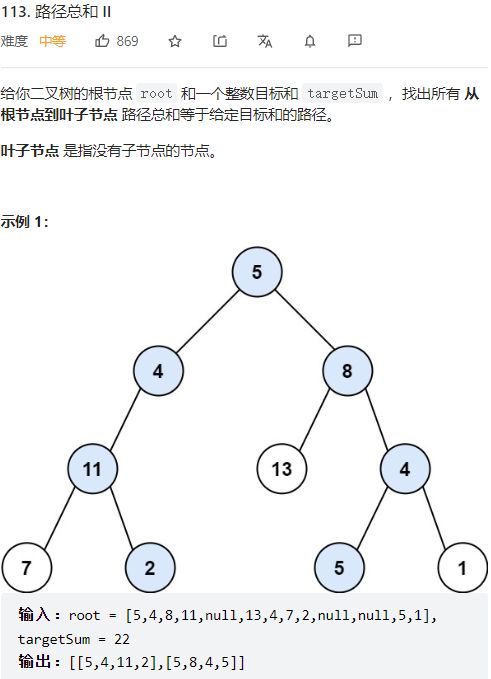
- 第113题 路经总和II
- 非自顶向下:
-
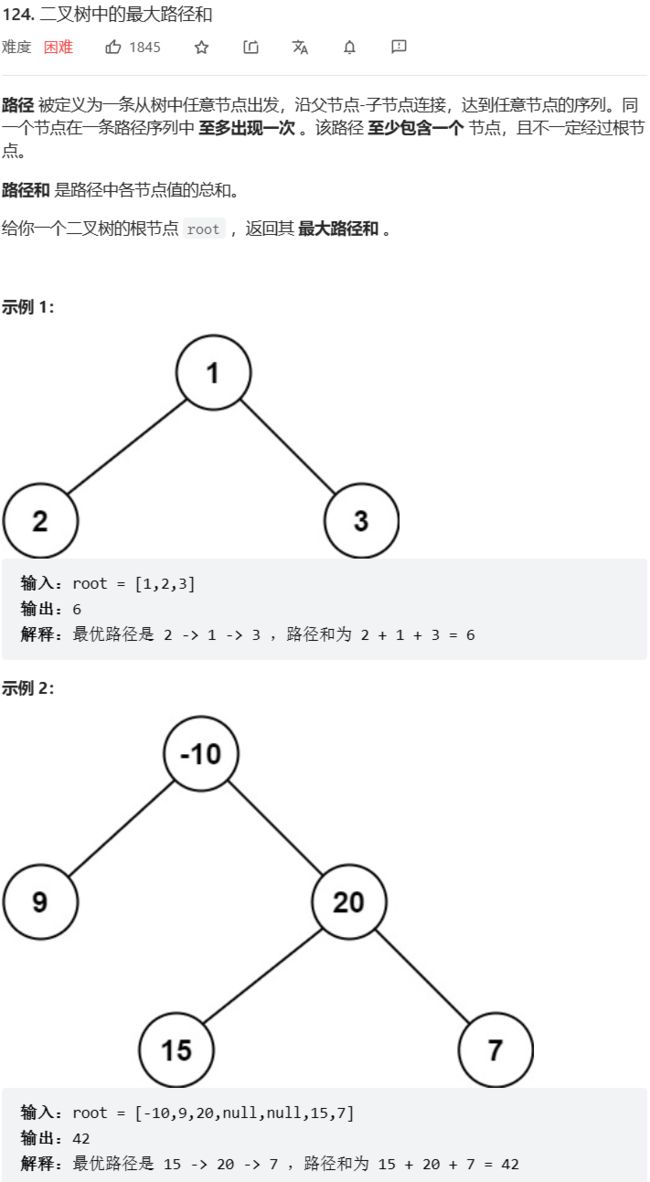
- *第124题 二叉树中的最大路径和
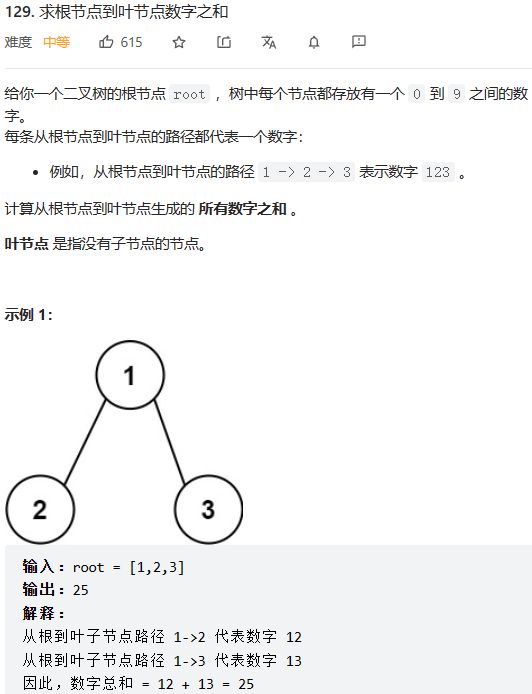
- 第129题 求根节点到叶子节点数字之和
-
- DFS(有返回值):
- BFS+队列:
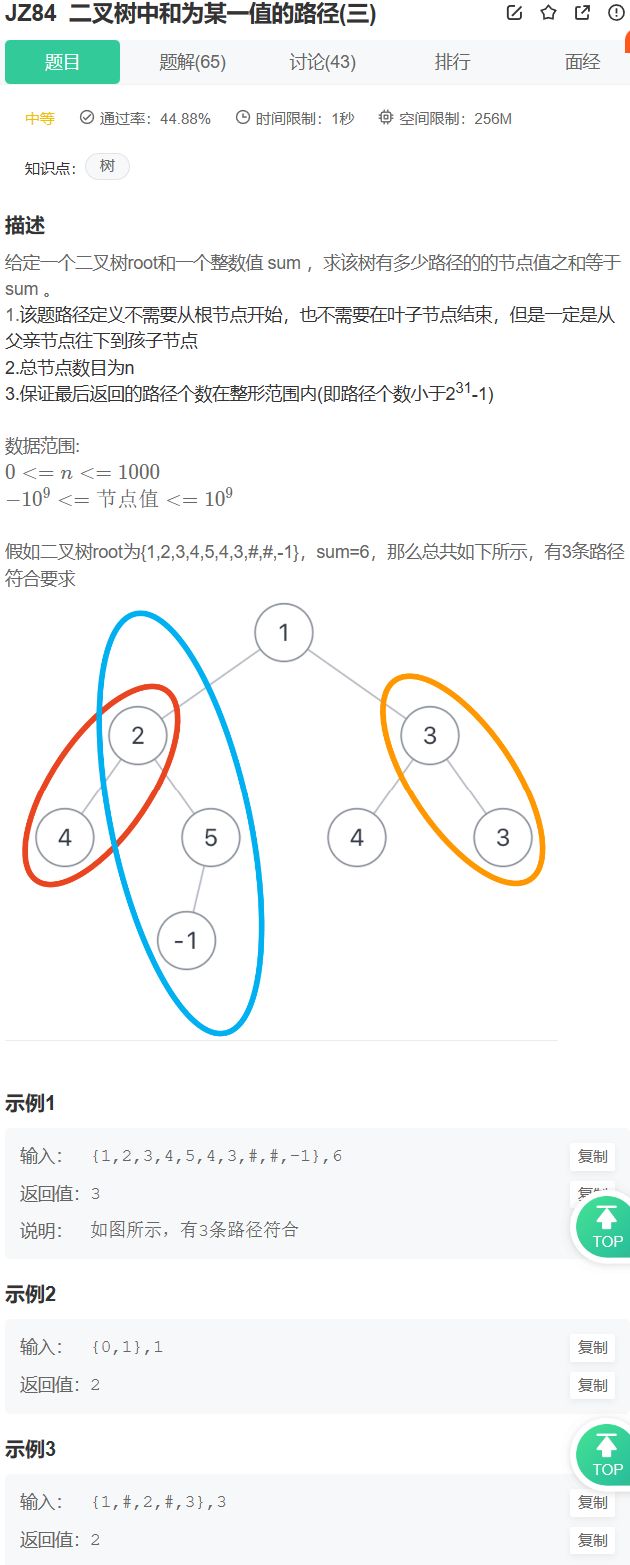
- 二叉树中和为某一值的路径(三)
- 有序序列与二叉树相互转换:
-
- 第114题 二叉树展开为链表
-
- 借助额外的空间:
- 原地构建(经典):
- 第108题 有序数组转换为二叉搜索树
-
- 递归 / DFS(有返回值):
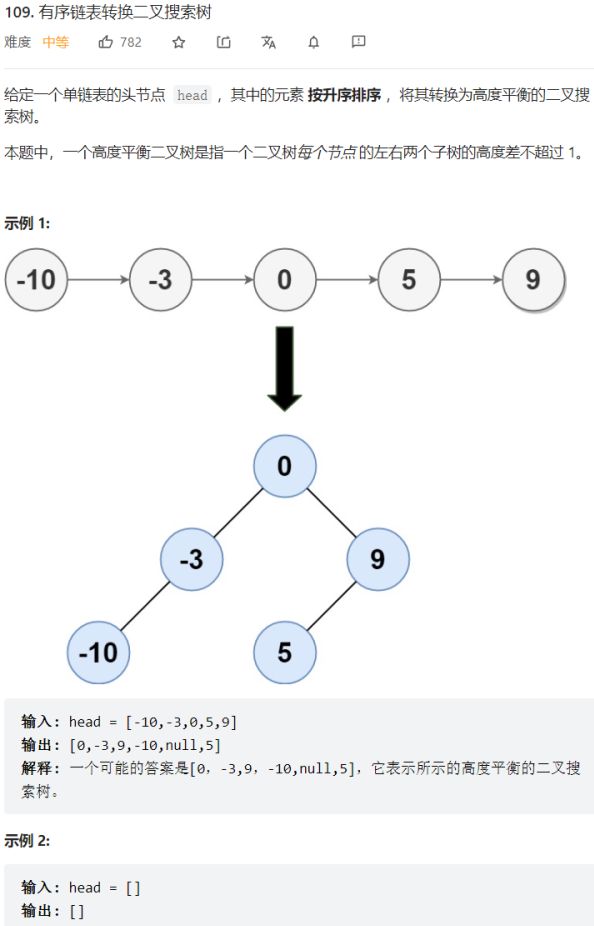
- 第109题 有序链表转换为二叉搜索树
-
- 递归 / DFS:
- 序列化二叉树:
-
- 前序序列 <--> 二叉树:
- 层序序列 <--> 二叉树:
- 第104题 二叉树的最大深度
-
- DFS(有返回值):
- BFS:
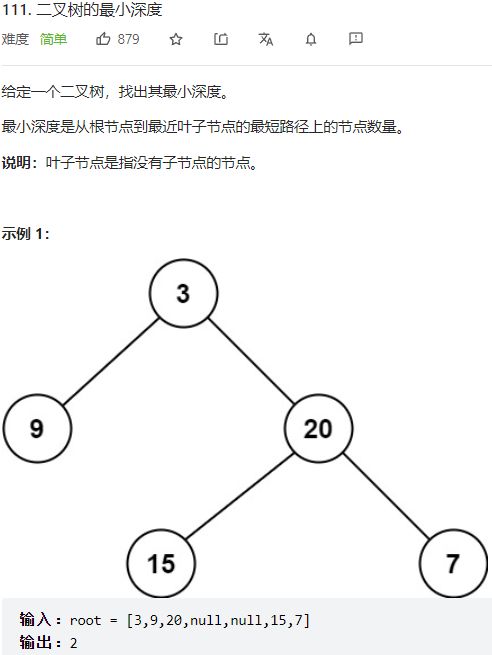
- 第111题 二叉树的最小深度
-
- BFS:
- _DFS:
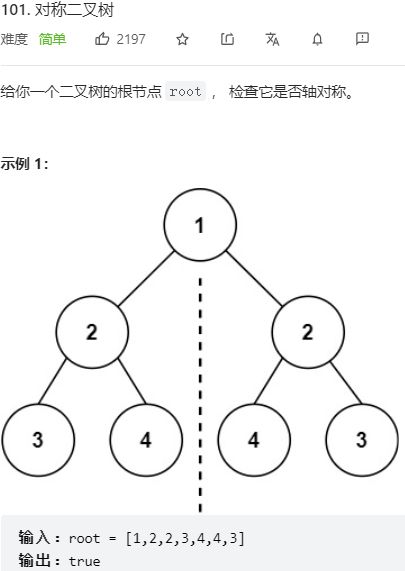
- 第101题 对称二叉树
-
- 递归/DFS(有返回值):
- 迭代BFS+队列:
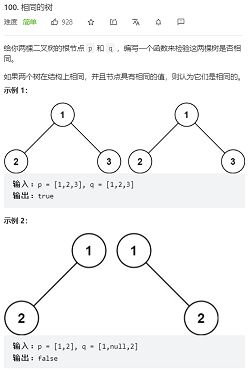
- 第100题 相同的树
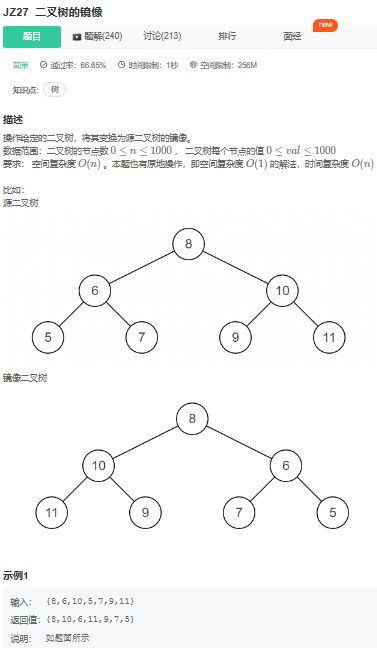
- 二叉树的镜像:
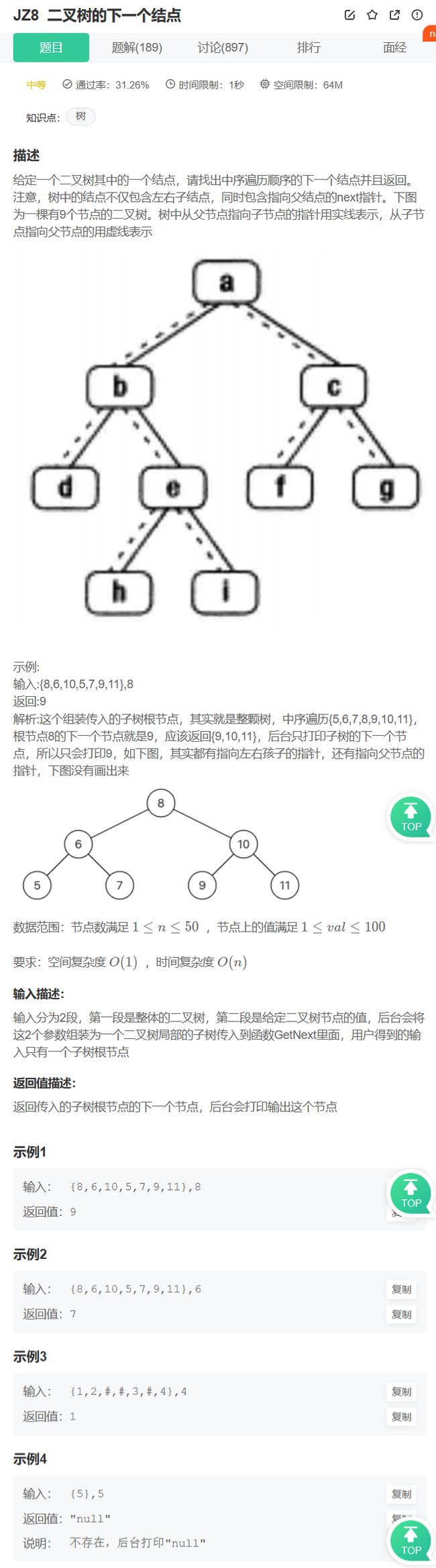
- 二叉树的下一个节点
- 二叉树的镜像
-
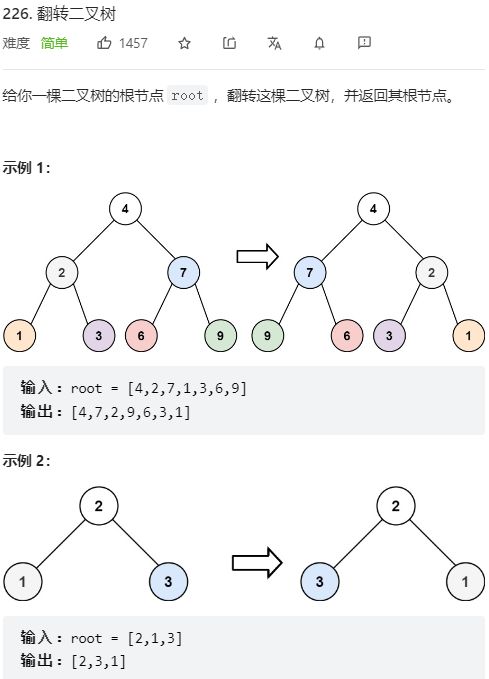
- 第226题 翻转二叉树
- 第951题 翻转等价二叉树
- 第236题 二叉树的最近公共祖先
-
- 找到根节点到p、q的两条路径,并得到其交点:
- 递归:(不太理解)
合并二叉树:
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == nullptr)
{
return t2;
}
if (t2 == nullptr)
{
return t1;
}
TreeNode* root = new TreeNode(t1->val + t2->val);
root->left = mergeTrees(t1->left, t2->left);
root->right = mergeTrees(t1->right, t2->right);
return root;
}
};
二叉搜索树相关
对二叉搜索树进行中序遍历时,得到的结果是一个有序的序列。
第98题 验证二叉搜索树

利用二叉搜索树的中序遍历必然为升序的特性,先生成中序遍历结果,再判断是否为升序。
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
// 二叉搜索树的中序遍历必然为升序的
bool isValidBST(TreeNode* root) {
vector<int> inorders;
inorderTraversal(root, inorders);
for (int i = 0; i < inorders.size() - 1; ++i)
{
if (inorders[i] >= inorders[i + 1])
{
return false;
}
}
return true;
}
vector<int> inorderTraversal(TreeNode* root, vector<int>& result)
{
stack<TreeNode*> simStack;
TreeNode* curr = root;
while (curr != nullptr || !simStack.empty())
{
// 先将curr结点的所有左节点入栈
while (curr != nullptr)
{
simStack.push(curr);
curr = curr->left;
}
// 此时curr没有左节点,即可放入result中,并将令curr=curr->right即开始访问curr的右节点
if (!simStack.empty())
{
curr = simStack.top(); simStack.pop();
result.push_back(curr->val);
curr = curr->right;
}
}
return result;
}
};
如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
stack<int> allNodes;
bool isBST;
public:
bool isValidBST(TreeNode* root) {
this->isBST = true;
validByInorderTraverse(root);
return this->isBST;
}
void validByInorderTraverse(TreeNode* node)
{
if (node == nullptr)
{
return;
}
validByInorderTraverse(node->left);
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (!this->allNodes.empty() && this->allNodes.top() >= node->val)
{
this->isBST = false;
return;
}
this->allNodes.push(node->val);
validByInorderTraverse(node->right);
}
};
第99题 恢复二叉搜索树
中序遍历得到遍历结果 -> 对其升序排列 -> 将升序后的结果重新挂载到二叉搜索树上。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<int> allNodes;
int usedIdx;
public:
void recoverTree(TreeNode* root) {
this->usedIdx = 0;
// 先中序遍历二叉搜索树:
InorderTraverse(root);
// 对中序遍历结果进行排序:
sort(allNodes.begin(), allNodes.end());
// 重新将排序后的中序遍历结果,赋给对应的二叉搜索树的对应位置
recoverByInorderTraverse(root);
}
void recoverByInorderTraverse(TreeNode* node)
{
if (node == nullptr)
{
return;
}
recoverByInorderTraverse(node->left);
node->val = this->allNodes[usedIdx++];
recoverByInorderTraverse(node->right);
}
void InorderTraverse(TreeNode* node)
{
if (node == nullptr)
{
return;
}
InorderTraverse(node->left);
this->allNodes.push_back(node->val);
InorderTraverse(node->right);
}
};
第1382题 将二叉搜索树变平衡
中序遍历+有序数组构建AVL树:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<int> nums; // 存放二叉搜索树的中序遍历结果,即升序序列
// 先将二叉树搜索树的中序遍历结果,存放在nums中
void inorderTraverse(TreeNode* root)
{
if (root == nullptr)
{
return;
}
inorderTraverse(root->left);
nums.push_back(root->val);
inorderTraverse(root->right);
}
public:
// 根据二叉搜索树的中序遍历结果,构造平衡二叉树AVL
TreeNode* balanceBST(TreeNode* root) {
inorderTraverse(root);
return subTree(0, nums.size() - 1);
}
TreeNode* subTree(int left, int right)
{
if (left > right)
{
return nullptr;
}
int mid = left + (right - left) / 2;
return (new TreeNode(nums[mid], subTree(left, mid - 1), subTree(mid + 1, right)));
}
};
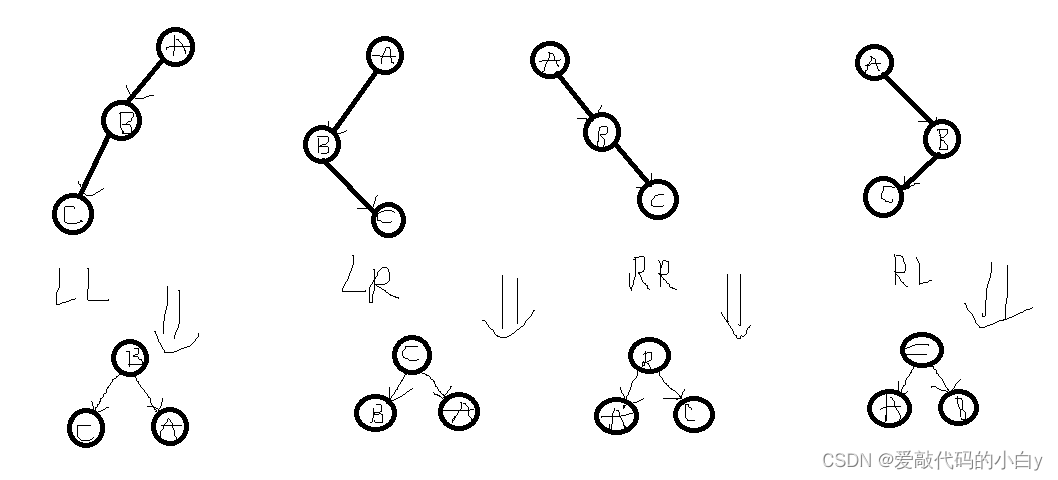
*通过递归,自下而上不断地旋转,直到二叉搜索树满足平衡树AVL的条件:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
/* 获取某个节点在树中的高度 */
unordered_map<TreeNode*, int> heights;
int GetHeight(TreeNode* root)
{
return (root == nullptr ? 0 : heights[root]);
}
int height(TreeNode* root)
{
if (root == nullptr)
{
return 0;
}
heights[root] = max(GetHeight(root->left), GetHeight(root->right)) + 1;
return heights[root];
}
/*
四种旋转构型:LL、LR、RR、RL
参数node是三层构型中的爷爷结点
*/
TreeNode* ll_rotate(TreeNode* node)
{
// 先调整交换后,node和node->left结点的高度的变化
// heights[node] = max(heights[node->right], heights[node->left->right]) + 1;
// heights[node->left] = max(heights[node], heights[node->left->left]) + 1;
// 旋转树,即调整结点的关系
TreeNode* tmp = node->left;
node->left = tmp->right;
tmp->right = node;
return tmp;
}
TreeNode* rr_rotate(TreeNode* node)
{
// // 先调整交换后,node和node->left结点的高度的变化
// heights[node] = max(heights[node->left], heights[node->right->left]) + 1;
// heights[node->left] = max(heights[node], heights[node->right->right]) + 1;
// 旋转树,即调整结点的关系
TreeNode* tmp = node->right;
node->right = tmp->left;
tmp->left = node;
return tmp;
}
TreeNode* lr_rotate(TreeNode* node)
{
node->left = rr_rotate(node->left);
return ll_rotate(node);
}
TreeNode* rl_rotate(TreeNode* node)
{
node->right = ll_rotate(node->right);
return rr_rotate(node);
}
public:
TreeNode* balanceBST(TreeNode* root) {
if (root == nullptr)
{
return nullptr;
}
root->left = balanceBST(root->left);
root->right = balanceBST(root->right);
int left_height = height(root->left), right_height = height(root->right);
if (left_height - right_height > 1) // 为LL/LR旋转
{
if (right_height >= height(root->left->left))
{
root = lr_rotate(root);
}
else
{
root = ll_rotate(root);
}
}
else if (right_height - left_height > 1) // 为RR/RL旋转
{
if (left_height >= height(root->right->right))
{
root = rl_rotate(root);
}
else
{
root = rr_rotate(root);
}
}
// 到这里时,需要再重新检查一遍
root->left = rebalanceBST(root->left);
root->right = rebalanceBST(root->right);
root = rebalanceBST(root);
return root;
}
private:
TreeNode* rebalanceBST(TreeNode* root) {
if (height(root) <= 1)
{
return root;
}
int left_height = height(root->left), right_height = height(root->right);
if (left_height - right_height > 1) // LL / LR旋转
{
if (height(root->left->right) >= height(root->left->left))
{
root = lr_rotate(root);
}
else
{
root = ll_rotate(root);
}
}
else if (right_height - left_height > 1) // RR / RL旋转
{
if (height(root->right->left) >= height(root->right->right))
{
root = rl_rotate(root);
}
else
{
root = rr_rotate(root);
}
}
// 到这里时,需要再重新检查一遍
root->left = rebalanceBST(root->left);
root->right = rebalanceBST(root->right);
root = rebalanceBST(root);
return root;
}
};
第938题 二叉搜索树的范围和
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<int> rangeBST;
void getRangeBST(TreeNode* root, int low, int high)
{
if (root == nullptr)
{
return;
}
if (low < root->val)
{
getRangeBST(root->left, low, high);
}
if (low <= root->val && root->val <= high)
{
rangeBST.push_back(root->val);
}
if (high > root->val)
{
getRangeBST(root->right, low, high);
}
}
public:
int rangeSumBST(TreeNode* root, int low, int high) {
// 先得到整个二叉搜索树中,满足[low, high]范围的所有结点的值,并存放在rangeBST中
getRangeBST(root, low, high);
// 对rangeBST中所有元素进行求和
return accumulate(rangeBST.begin(), rangeBST.end(), 0);
}
};
第110题 高度平衡的二叉树
自顶向下递归:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
// 可以通过将之前计算过的结点的高度保存,来降低复杂度
unordered_map<TreeNode*, int> heights;
int height(TreeNode* root)
{
if (root == nullptr)
{
return 0;
}
if (heights.find(root) != heights.end())
{
return heights[root];
}
heights[root] = max(height(root->left), height(root->right)) + 1;
return heights[root];
}
public:
// DFS,即自顶向下递归
bool isBalanced(TreeNode* root) {
if (root == nullptr)
{
return true;
}
return (abs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right));
}
};
自底向上递归:
class Solution {
private:
// height∈{[1, ~), -1} : -1表示该节点的左右不平衡;其他值表示节点的左右平衡且该值为该节点的高度
int height(TreeNode* node) {
if (node == nullptr)
{
return 0;
}
int left_height = height(node->left);
if (left_height == -1)
{
return -1;
}
int right_height = height(node->right);
if (right_height == -1)
{
return -1;
}
return ((abs(left_height - right_height) <= 1) ? (max(left_height, right_height) + 1) : -1);
}
public:
bool isBalanced(TreeNode* root) {
return (height(root) >= 0);
}
};
不同的二叉搜索树:
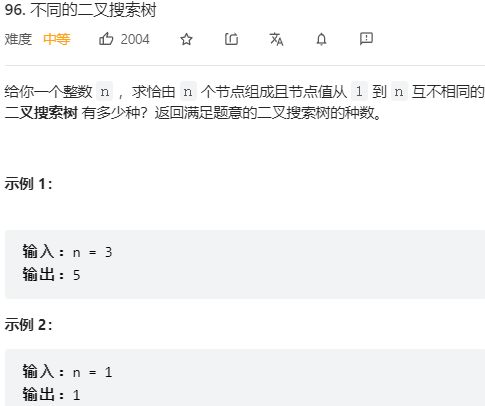
第96题 不同的二叉搜索树
动态规划DP:
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1; dp[1] = 1;
for (int i = 2; i <= n; ++i)
{
for (int j = 1; j <= i; ++j)
{
dp[i] += (dp[j - 1] * dp[i - j]);
}
}
return dp[n];
}
};
*第95题 不同的二叉搜索树II
递归回溯:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<TreeNode*> BSTs;
public:
vector<TreeNode*> generateTrees(int n) {
if (n <= 0)
{
return {};
}
return generateTree(1, n);
}
// 返回序列 [start,end] 生成的所有可行的二叉搜索树
vector<TreeNode*> generateTree(int start, int end)
{
if (start > end)
{
return { nullptr };
}
vector<TreeNode*> allBSTs;
// 分别找到以[start,end]中每个数为根节点的所有二叉搜索树的组合
for (int i = start; i <= end; ++i)
{
// [start, i-1]区间内元素,能形成的所有二叉搜索树的根节点的数组
vector<TreeNode*> leftSubtrees = generateTree(start, i - 1);
// [i+1, end]区间内元素,能形成的所有二叉搜索树的根节点的数组
vector<TreeNode*> rightSubtrees = generateTree(i + 1, end);
// 从可行左子树集合、可行右子树集合中,各选一棵拼接到根节点上,并将生成的二叉搜索树放入答案数组即可
for (auto leftSubtree : leftSubtrees)
{
for (auto rightSubtree : rightSubtrees)
{
allBSTs.push_back(new TreeNode(i, leftSubtree, rightSubtree));
}
}
}
return allBSTs;
}
};
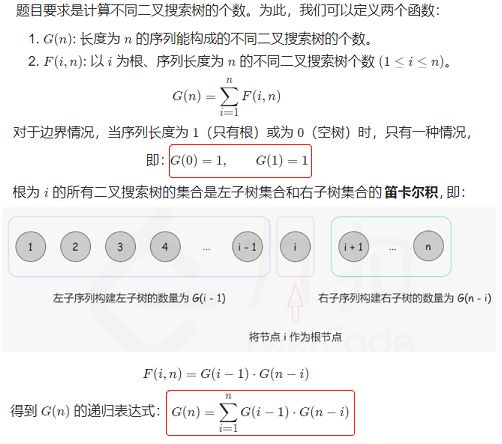
*第222题 完全二叉树的节点个数
层序遍历/深度搜索,时间复杂度为O(n)。
二分法+深度搜索DFS,时间复杂度为O(logn)。
注意:完全二叉树,从根节点到(有层序编号的)目标节点的路径寻找。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr)
{
return 0;
}
int _height = height(root);
int level = _height - 1;
// 完全二叉树的总的可能节点个数范围 [2^(height - 1), 2^height - 1](范围的上下界,按照层序遍历的结果给出)
// 通过二分法查找,直到找到某个节点上述范围中,分界点(存在与不存在的分界点)
int left = 1 << level, right = (1 << (level + 1)) - 1;
while (left < right)
{
int mid = left + ((right - left + 1) >> 1);
if (IsExits(root, level, mid) == true) {
left = mid;
} else {
right = mid - 1;
}
}
return left;
}
private:
/* 难点!!! */
// 1、将目标叶子节点的编号转换为二进制数,去掉最高位的1,得到一个长度为k-1的二进制数
// 2、从根节点开始遍历该二进制数的每一位,如果该位是1,则向右子节点方向移动,否则向左子节点方向移动
bool IsExits(TreeNode* root, int level, int k)
{
int bits = 1 << (level - 1);
TreeNode* node = root;
while (node != nullptr && bits > 0)
{
if ((bits & k) == 0) {
node = node->left;
} else {
node = node->right;
}
bits >>= 1;
}
return node != nullptr;
}
// 计算完全二叉树的高度,第0层...,height = pow(2, n) + 1,其中n = 0、1、...
// 找到完全二叉树的最左下的节点所走的步数,即为完二叉树的高度
int height(TreeNode* root)
{
int steps = 0;
TreeNode* curr = root;
while (curr != nullptr)
{
++steps;
curr = curr->left;
}
return steps;
}
};
树的子结构:
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
if (pRoot2 == nullptr || pRoot1 == nullptr) // 空树不是任意一个树的子结构
{
return false;
}
return recursive(pRoot1, pRoot2) || HasSubtree(pRoot1->left, pRoot2) || HasSubtree(pRoot1->right, pRoot2);
}
private:
bool recursive(TreeNode* root1, TreeNode* root2) {
if (root2 == nullptr)
{
return true;
}
else if (root1 != nullptr)
{
if (root1->val == root2->val)
{
return recursive(root1->left, root2->left) && recursive(root1->right, root2->right);
}
return false;
}
else
{
return false;
}
}
};
与树的遍历有关:
第199题 二叉树的右视图
层序遍历+队列:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<int> results;
public:
// 层序遍历:需要“尾插”“头取”“访问队尾元素”,故用队列来实现
vector<int> rightSideView(TreeNode* root) {
if (root == nullptr)
{
return results;
}
queue<TreeNode*> levelOrders;
levelOrders.push(root);
results.push_back(root->val);
while (true)
{
queue<TreeNode*> _levelOrders;
while (!levelOrders.empty())
{
TreeNode* node = levelOrders.front(); levelOrders.pop();
if (node->left != nullptr)
{
_levelOrders.push(node->left);
}
if (node->right != nullptr)
{
_levelOrders.push(node->right);
}
}
if (!_levelOrders.empty()) {
levelOrders = _levelOrders;
results.push(levelOrders.back()->val);
} else {
break;
}
}
return results;
}
};
第230题 二叉搜索树中第k小的数
中序遍历+递归:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 中序遍历:递归完成
int kthSmallest(TreeNode* root, int k) {
DFS(root);
int count = 0;
for (auto middleOrder_ : middleOrder)
{
if (++count == k)
{
return middleOrder_;
}
}
return -1;
}
private:
vector<int> middleOrder;
void DFS(TreeNode* node)
{
if (node == nullptr)
{
return;
}
DFS(node->left);
middleOrder.push_back(node->val);
DFS(node->right);
}
};
中序遍历+迭代(无需全树遍历):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
stack<TreeNode*> middleOrder;
middleOrder.push(root);
TreeNode* tmp = root;
while (!middleOrder.empty() && tmp != nullptr)
{
tmp = middleOrder.top(); middleOrder.pop();
while (tmp != nullptr)
{
middleOrder.push(tmp);
tmp = tmp->left;
}
--k;
if (k == 0)
{
break;
}
tmp = middleOrder.top(); middleOrder.pop();
middleOrder.push(tmp->right);
}
return middleOrder.top()->val;
}
};
第144题 二叉树的前序遍历
递归/DFS:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<int> results;
public:
// 递归得到前序遍历结果:
vector<int> preorderTraversal(TreeNode* root) {
DFS(root);
return results;
}
void DFS(TreeNode* root)
{
if (root == nullptr)
{
return;
}
results.push_back(root->val);
DFS(root->left);
DFS(root->right);
}
};
迭代(借助栈):
class Solution {
public:
// 迭代得到前序遍历结果:
vector<int> preorderTraversal(TreeNode* root) {
if (root == nullptr)
{
return {};
}
vector<int> results;
stack<TreeNode*> preorderTraverseProcess;
preorderTraverseProcess.push(root);
while (!preorderTraverseProcess.empty())
{
TreeNode* node = preorderTraverseProcess.top(); preorderTraverseProcess.pop();
results.push_back(node->val);
if (node->right != nullptr)
{
preorderTraverseProcess.push(node->right);
}
if (node->left != nullptr)
{
preorderTraverseProcess.push(node->left);
}
}
return results;
}
};
第94题 二叉树的中序遍历
递归形式:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
DFS(root, result);
return result;
}
void DFS(TreeNode* root, vector<int>& result)
{
if (root == nullptr)
{
return;
}
DFS(root->left, result);
result.push_back(root->val);
DFS(root->right, result);
}
};
_迭代形式:
递归和迭代两种方式是等价的,区别在于递归隐式地维护了一个栈,而在迭代的时需要显式地将这个栈模拟出来,其他都相同。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> simStack;
TreeNode* curr = root;
while (curr != nullptr || !simStack.empty())
{
// 先将curr结点的所有左节点入栈
while (curr != nullptr)
{
simStack.push(curr);
curr = curr->left;
}
// 此时curr没有左节点,即可放入result中,并将令curr=curr->right即开始访问curr的右节点
if (!simStack.empty())
{
curr = simStack.top(); simStack.pop();
result.push_back(curr->val);
curr = curr->right;
}
}
return result;
}
};
第145题 二叉树的后序遍历
递归/DFS:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<int> results;
public:
// 递归得到后序遍历结果:
vector<int> postorderTraversal(TreeNode* root) {
DFS(root);
return results;
}
void DFS(TreeNode* root)
{
if (root == nullptr)
{
return;
}
DFS(root->left);
DFS(root->right);
results.push_back(root->val);
}
};
迭代:
class Solution {
public:
// 迭代得到后序遍历结果:
vector<int> postorderTraversal(TreeNode* root) {
if (root == nullptr)
{
return {};
}
vector<int> results;
stack<TreeNode*> postorderTraverseProcess; postorderTraverseProcess.push(root);
TreeNode* curr = nullptr;
while (!postorderTraverseProcess.empty())
{
curr = postorderTraverseProcess.top(); postorderTraverseProcess.pop();
if (curr != nullptr)
{
// 每次在给栈中,压入父节点时,都要另外再压入一个nullptr数据;用于表示nullptr数据的下一个数据是一个父节点;
postorderTraverseProcess.push(curr); postorderTraverseProcess.push(nullptr);
if (curr->right != nullptr)
{
postorderTraverseProcess.push(curr->right);
}
if (curr->left != nullptr)
{
postorderTraverseProcess.push(curr->left);
}
}
else
{
// 只有在父节点没有子节点,即是叶子节点时,才能在出栈后将其值存入results中
curr = postorderTraverseProcess.top(); postorderTraverseProcess.pop();
results.push_back(curr->val);
}
}
return results;
}
};
后序遍历相关:
验证二叉搜索树的后序遍历序列
class Solution {
public:
// 输入序列的任意两个数字都互不相同
bool VerifySquenceOfBST(vector<int> sequence) {
if (sequence.empty()) // 空树不是二叉搜索树
{
return false;
}
return divideAndConquer(sequence, 0, sequence.size() - 1);
}
// 检查sequence[left, ..., right]之前的序列是否为二叉搜索树的后序序列
bool divideAndConquer(const vector<int>& sequence, int left, int right)
{
if (left >= right)
{
return true;
}
int& rootIdx = right; int& leftIdx = left; int rightIdx = leftIdx;
// 从leftIdx开始,找到右子树的边界rightIdx
while (rightIdx < rootIdx && sequence[rightIdx] < sequence[rootIdx])
{
++rightIdx;
}
// 验证sequence[rightIdx, ..., rootIdx - 1]是否均为大于sequence[rootIdx]
for (int i = rightIdx; i < rootIdx; ++i)
{
if (sequence[i] < sequence[rootIdx])
{
return false;
}
}
// 此时索引对应的关系:左子树[leftIdx, rightIdx - 1],右子树[rightIdx, rootIdx - 1],根节点rootIdx
//,故开始分别验证左右子树是否为二叉搜索树
return divideAndConquer(sequence, leftIdx, rightIdx - 1) && divideAndConquer(sequence, rightIdx, rootIdx - 1);
}
};
第102题 二叉树的层序遍历
借助队列:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (root == nullptr)
{
return {};
}
vector<vector<int>> levelOrderResult;
queue<TreeNode*> traverseProcess;
traverseProcess.push(root);
while (!traverseProcess.empty())
{
vector<int> result;
int size = traverseProcess.size(); // 记录上层中的结点数
for (int i = size; i > 0; --i)
{
TreeNode* node = traverseProcess.front(); traverseProcess.pop();
if (node != nullptr)
{
if (node->left != nullptr)
{
traverseProcess.push(node->left);
}
if (node->right != nullptr)
{
traverseProcess.push(node->right);
}
result.push_back(node->val);
}
}
levelOrderResult.push_back(result);
}
return levelOrderResult;
}
};
层序遍历相关:
第107题 二叉树的层序遍历II
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
if (root == nullptr)
{
return {};
}
stack<vector<int>> results;
queue<TreeNode*> traverseLevelOrder;
traverseLevelOrder.push(root); results.push({root->val});
while (!traverseLevelOrder.empty())
{
vector<int> result;
int size = traverseLevelOrder.size(); // 记录上层中的结点数
for (int i = size; i > 0; --i)
{
TreeNode* node = traverseLevelOrder.front(); traverseLevelOrder.pop();
if (node->left != nullptr)
{
result.push_back(node->left->val);
traverseLevelOrder.push(node->left);
}
if (node->right != nullptr)
{
result.push_back(node->right->val);
traverseLevelOrder.push(node->right);
}
}
if (result.empty()) // 避免上一层的父节点的子节点为空的现象
{
break;
}
results.push(result);
}
// 将results栈,逐个弹出,存入levelOrderBottomResults中
vector<vector<int>> levelOrderBottomResults;
while (!results.empty())
{
levelOrderBottomResults.push_back(results.top());
results.pop();
}
return levelOrderBottomResults;
}
};
第103题 二叉树的锯齿形层序遍历
层序遍历+判断:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
if (root == nullptr)
{
return {};
}
vector<vector<int>> results;
queue<TreeNode*> inorderTraverse;
inorderTraverse.push(root); results.push_back({root->val});
while (!inorderTraverse.empty())
{
vector<int> result;
int size = inorderTraverse.size();
for (int i = size; i > 0; --i)
{
TreeNode* node = inorderTraverse.front(); inorderTraverse.pop();
if (node->left != nullptr)
{
inorderTraverse_tmp.push(node->left);
result.push_back(node->left->val);
}
if (node->right != nullptr)
{
inorderTraverse_tmp.push(node->right);
result.push_back(node->right->val);
}
}
if (!result.empty())
{
if (results.size() % 2 == 1)
{
reverse(result.begin(), result.end());
}
results.push_back(result);
}
}
return results;
}
};
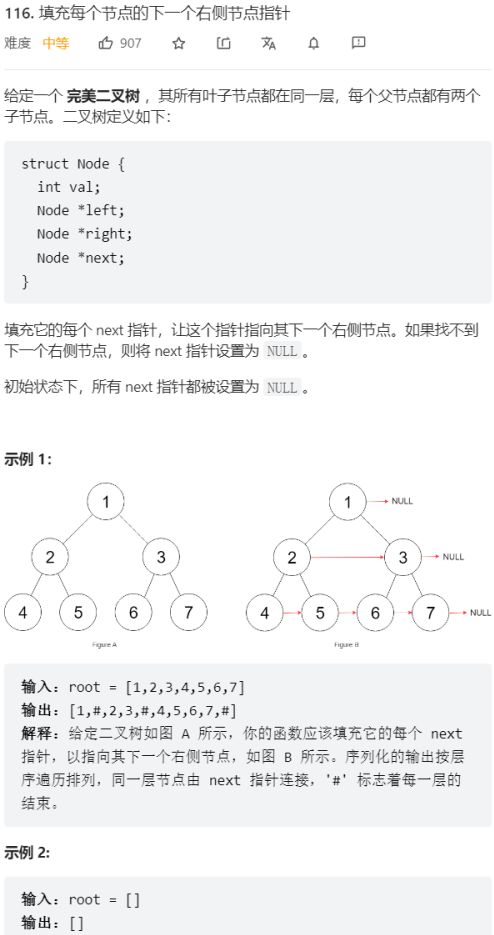
第116题 填充每个节点的下一个右侧结点指针
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr)
{
return nullptr;
}
queue<Node*> levelorder;
levelorder.push(root);
while (!levelorder.empty())
{
int size = levelorder.size();
for (int i = 0; i < size; ++i)
{
Node* node = levelorder.front(); levelorder.pop();
if (i != size - 1)
{
node->next = levelorder.front();
}
if (node->left != nullptr)
{
levelorder.push(node->left);
}
if (node->right != nullptr)
{
levelorder.push(node->right);
}
}
}
return root;
}
};
根据遍历结果重建二叉树:
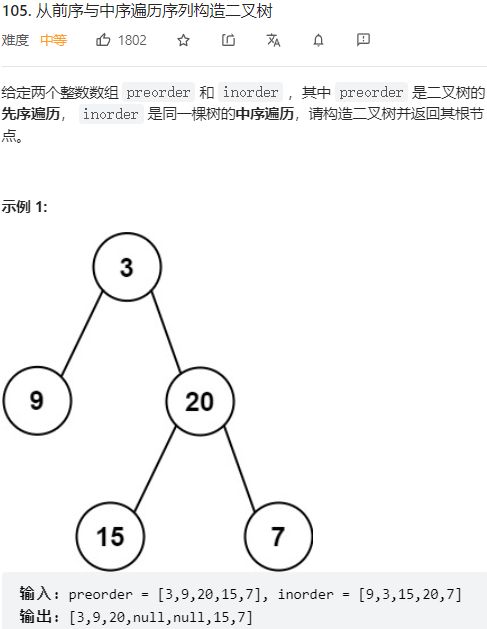
*第105题 从前序与中序遍历序列构造二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return buildBinaryTree_(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1);
}
TreeNode* buildBinaryTree_(const vector<int>& preOrder, int left1, int right1, const vector<int>& inOrder, int left2, int right2)
{
if (left1 > right1 || left2 > right2)
{
return nullptr;
}
TreeNode* root = new TreeNode(preOrder[left1]);
int rootIndex_inOrder = 0;
for (int i = left2; i <= right2; ++i)
{
if (inOrder[i] == preOrder[left1])
{
rootIndex_inOrder = i;
break;
}
}
int leftsize = rootIndex_inOrder - left2;
int rightsize = right2 - rootIndex_inOrder;
root->left = buildBinaryTree_(preOrder, left1 + 1, left1 + leftsize, inOrder, left2, rootIndex_inOrder - 1);
root->right = buildBinaryTree_(preOrder, right1 - rightsize + 1, right1, inOrder, rootIndex_inOrder + 1, right2);
return root;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 将前序看作子树根节点的集合,前序的第一个元素是用来在inorder划分左右子树的,故可以用递归不断的向下构建二叉树
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
TreeNode* root = nullptr;
CreateBTByPreIn(&root, preorder.begin(), inorder.begin(), inorder.size());
return root;
}
private:
void CreateBTByPreIn(TreeNode** root, vector<int>::iterator preorder_iter, vector<int>::iterator inorder_iter, int size)
{
if (size == 0)
{
return;
}
(*root) = new TreeNode(*preorder_iter);
// 在inorder中,找到preorder[0]在的索引位置i
int i = 0;
auto tmp_inorder_iter = inorder_iter;
auto tmp_preorder_iter = preorder_iter;
while (*preorder_iter != *tmp_inorder_iter)
{
++tmp_inorder_iter;
++tmp_preorder_iter;
++i;
}
// 此时,左子树在inorder∈[inorder_iter, inorder_iter + i - 1]中
// 此时,右子树在inorder∈[tmp_inorder_iter + 1, inorder.end() - 1]中
CreateBTByPreIn(&((*root)->left), preorder_iter + 1, inorder_iter, i);
CreateBTByPreIn(&((*root)->right), tmp_preorder_iter + 1, tmp_inorder_iter + 1, size - 1 - i);
}
};
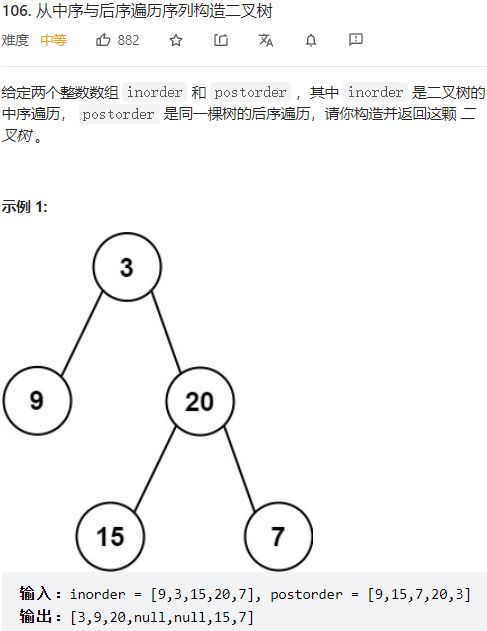
*第106题 从中序与后序遍历序列构造二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
// 记录所有节点值,对应的中序序列的索引
for (int i = 0; i < inorder.size(); ++i)
{
positions[inorder[i]] = i;
}
return buildBinaryTree_(inorder, 0, inorder.size() - 1, postorder, 0, postorder.size() - 1);
}
private:
unordered_map<int, int> positions;
TreeNode* buildBinaryTree_(const vector<int>& inOrder, int left1, int right1, const vector<int>& postOrder, int left2, int right2)
{
if (left1 > right1 || left2 > right2)
{
return nullptr;
}
int rootIndex_inOrder = positions[postOrder[right2]];
TreeNode* root = new TreeNode(postOrder[right2]);
root->left = buildBinaryTree_(inOrder, left1, rootIndex_inOrder - 1, postOrder, left2, left2 + rootIndex_inOrder - 1 - left1);
root->right = buildBinaryTree_(inOrder, rootIndex_inOrder + 1, right1, postOrder, left2 + rootIndex_inOrder - 1 - left1 + 1, right2 - 1);
return root;
}
};
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
TreeNode* root = nullptr;
InAndPostOrderToBT(&root, inorder, postorder, inorder.size());
return root;
}
void InAndPostOrderToBT(TreeNode** root, vector<int> inorder, vector<int> postorder, int size)
{
if (size == 0) { return; } // 递归结束的条件
(*root) = new TreeNode(postorder[size - 1]);
// 找到根节点元素在中序中的位置i
int i = 0;
vector<int>::iterator inorder_iter = inorder.begin();
vector<int>::iterator postorder_iter = postorder.begin();
while (inorder[i] != postorder[size - 1])
{
++inorder_iter;
++postorder_iter;
++i;
}
InAndPostOrderToBT(&((*root)->left), inorder, postorder, i); // 左子树递归求解
++inorder_iter;
InAndPostOrderToBT(&((*root)->right), vector<int>(inorder_iter, inorder.end()), vector<int>(postorder_iter, postorder.end()), size - i - 1); // 右子树递归求解
}
};
二叉树路径相关:
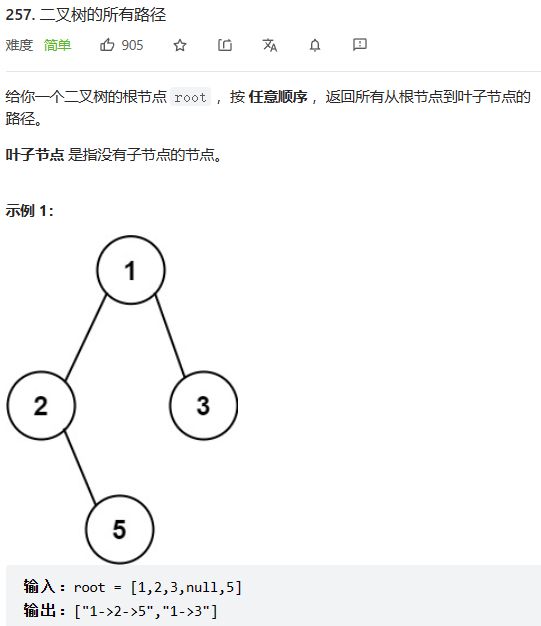
第257题 二叉树的所有路径
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<string> results;
public:
vector<string> binaryTreePaths(TreeNode* root) {
if (root == nullptr)
{
return {};
}
if (root->left == nullptr && root->right == nullptr)
{
return (vector<string>){ to_string(root->val) };
}
DFS(root->left, to_string(root->val));
DFS(root->right, to_string(root->val));
return results;
}
private:
void DFS(TreeNode* node, string result)
{
if (node == nullptr)
{
return;
}
result += ("->" + to_string(node->val));
if (node->left == nullptr && node->right == nullptr)
{
results.push_back(result);
return;
}
DFS(node->left, result);
DFS(node->right, result);
}
};
二叉树的路径和:
自顶向下:
第112题 路径总和
递归 / DFS:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr)
{
return false;
}
if (root->left == nullptr && root->right == nullptr)
{
return (targetSum == root->val);
}
return (hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val));
}
};
第113题 路经总和II
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<vector<int>> routes;
public:
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<int> route;
DFS(root, route, targetSum);
return routes;
}
void DFS(TreeNode* root, vector<int> route, int residual_sum)
{
if (root == nullptr)
{
return;
}
if (root->left == nullptr && root->right == nullptr)
{
if (root->val == residual_sum)
{
route.push_back(root->val);
routes.push_back(route);
}
return;
}
route.push_back(root->val);
DFS(root->left, route, residual_sum - root->val);
DFS(root->right, route, residual_sum - root->val);
return;
}
};
非自顶向下:
*第124题 二叉树中的最大路径和
递归:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int result = INT_MIN;
public:
int maxPathSum(TreeNode* root) {
Recursion(root);
return result;
}
// 从root节点出发的最大的路径和
int Recursion(TreeNode* root)
{
if (root == nullptr)
{
return 0;
}
// 如果当前root节点的左右子节点,出现了最大路径和 < 0,则直接将其置零(避免负收益)
int left = max(Recursion(root->left), 0);
int right = max(Recursion(root->right), 0);
// result = 根节点的值 + 左边子节点的最大路径和(非负) + 右边子节点的最大路径和(非负)
result = max(result, left + right + root->val);
// DFS(TreeNode* root)函数的返回值,表示从 root出发 走 左或右子节点 能获得的最大路径和
return root->val + max(left, right);
}
};
第129题 求根节点到叶子节点数字之和
DFS(有返回值):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
/* 方法一:自己写的版本 */
class Solution {
private:
vector<vector<int>> results;
public:
int sumNumbers(TreeNode* root) {
// 先找到二叉树的所有路径
DFS(root, {});
// 对每条路径进行计算
int sum = 0;
for (int i = 0; i < results.size(); ++i)
{
int bitNum = results[i].size();
for (int j = 0; j < bitNum; ++j)
{
sum += results[i][j] * pow(10, bitNum - j - 1);
}
}
return sum;
}
void DFS(TreeNode* node, vector<int> result)
{
if (node == nullptr)
{
return;
}
result.push_back(node->val);
if (node->left == nullptr && node->right == nullptr)
{
results.push_back(result);
return;
}
DFS(node->left, result);
DFS(node->right, result);
}
};
/* 方法二:难以想到 */
class Solution {
private:
int sum;
public:
int sumNumbers(TreeNode* root) {
return DFS(root, 0);
}
int DFS(TreeNode* node, int prevSum)
{
if (node == nullptr)
{
return 0;
}
int sum = (prevSum * 10 + node->val);
if (node->left == nullptr && node->right == nullptr)
{
return sum;
}
return DFS(node->left, sum) + DFS(node->right, sum);
}
};
BFS+队列:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int sum;
public:
int sumNumbers(TreeNode* root) {
sum = 0;
// 用两个队列来分别保存遍历过的节点和该节点前其所在路径的数字和(一一对应)
queue<TreeNode*> levelOrders; levelOrders.push(root);
queue<int> numlevelOrders; numlevelOrders.push(root->val);
while (!levelOrders.empty())
{
TreeNode* currNode = levelOrders.front(); levelOrders.pop();
int currNodePathSum = numlevelOrders.front(); numlevelOrders.pop();
if (currNode->left != nullptr)
{
levelOrders.push(currNode->left);
numlevelOrders.push(currNodePathSum * 10 + currNode->left->val);
}
if (currNode->right != nullptr)
{
levelOrders.push(currNode->right);
numlevelOrders.push(currNodePathSum * 10 + currNode->right->val);
}
if (currNode->left == nullptr && currNode->right == nullptr)
{
sum += currNodePathSum;
}
}
return sum;
}
};
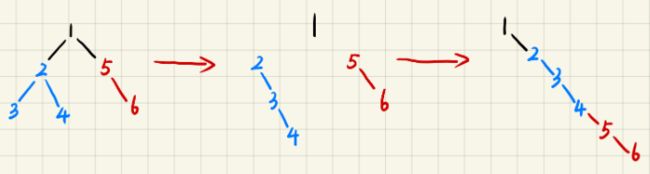
二叉树中和为某一值的路径(三)
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
private:
int result;
// 查询以某个节点为根节点,是否存在一条和为sum的路径,存在则result+1
void DFS(TreeNode* root, int sum)
{
if (root == nullptr)
{
return;
}
if (sum == root->val)
{
++result;
}
DFS(root->left, sum - root->val);
DFS(root->right, sum - root->val);
}
public:
Solution() : result(0)
{}
// 从整棵树的根节点root开始,以每个节点为路径的起点传入DFS函数,判断路径是否存在
int FindPath(TreeNode* root, int sum) {
if (root == nullptr)
{
return result;
}
// 以root为新路径起点,查找和为sum的路径是否存在
DFS(root, sum);
// 分别以root的左、右子节点为新路径的起点,查找和为sum的路径是否存在
FindPath(root->left, sum);
FindPath(root->right, sum);
return result;
}
};
有序序列与二叉树相互转换:
第114题 二叉树展开为链表
借助额外的空间:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
vector<TreeNode*> preorder;
public:
// 将preorder中的各个节点串联起来,每个节点的left=nullptr
void flatten(TreeNode* root) {
DFS(root);
int size = preorder.size();
if (size == 0) {
root = nullptr;
} else if (size == 1) {
root = preorder[0];
} else {
for (int i = 0; i < size - 1; ++i)
{
preorder[i]->left = nullptr;
preorder[i]->right = preorder[i + 1];
}
root = preorder[0];
}
}
// 前序遍历:
void DFS(TreeNode* bt_root)
{
if (bt_root == nullptr)
{
return;
}
preorder.push_back(bt_root);
DFS(bt_root->left);
DFS(bt_root->right);
}
};
原地构建(经典):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 原地构造:在写递归时,“内部调用时只关注函数的输入和输出,并不用关注内部的逻辑实现”
void flatten(TreeNode* root) {
if (root == nullptr)
{
return;
}
// 将root的左/右子树都变成链表
flatten(root->left);
flatten(root->right);
// root连接root->left的链表,root->left链表的末端连接的root->right的链表
TreeNode* tmp = root->right;
if (root->left == nullptr)
{
return;
}
root->right = root->left;
TreeNode* tmp2 = root->left;
root->left = nullptr;
while (tmp2->right != nullptr)
{
tmp2 = tmp2->right;
}
tmp2->right = tmp;
tmp2->left = nullptr;
}
};
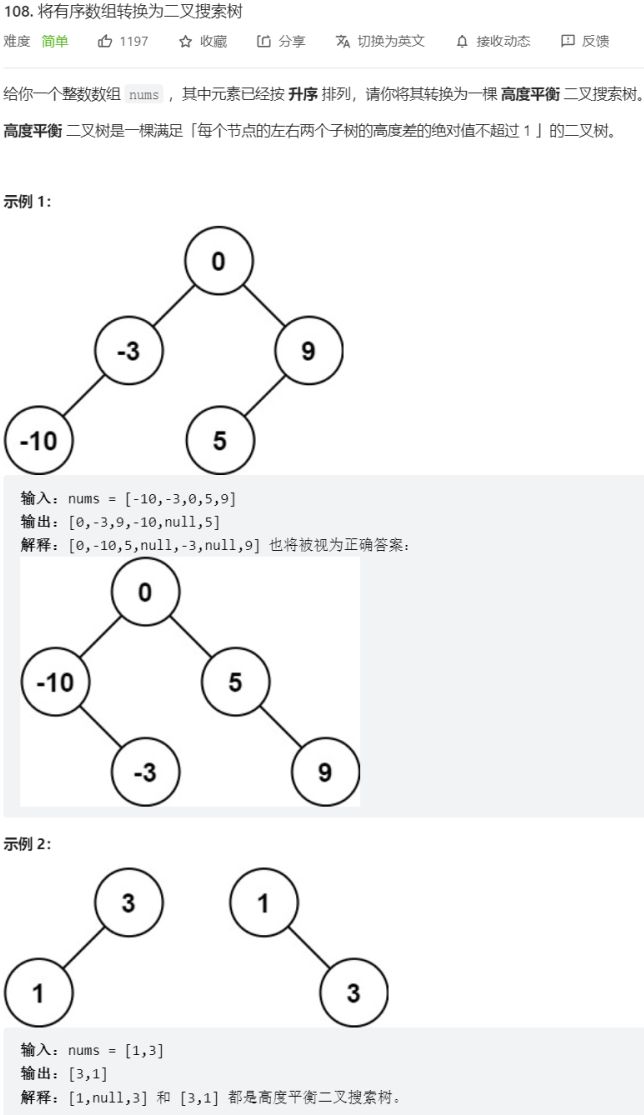
第108题 有序数组转换为二叉搜索树
递归 / DFS(有返回值):
有序数组 --> 二叉搜索树的两种写法。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return subTree(nums, 0, nums.size() - 1);
}
TreeNode* subTree(vector<int>& nums, int left, int right)
{
if (left > right) {
return nullptr;
}
// 为保证父节点出发,都是平衡二叉搜索树,即左右子节点的高度差<=1,故必须每次用[left, right]的中间mid并所在位置的值作为结点值
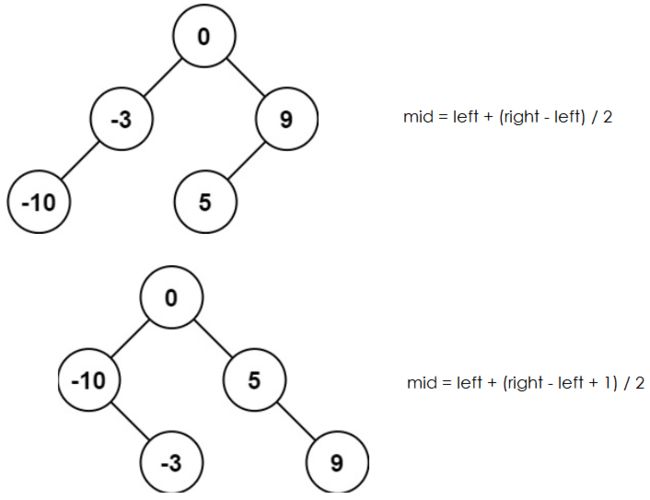
int mid = (left + right) / 2;
return new TreeNode(nums[mid], subTree(nums, left, mid - 1), subTree(nums, mid + 1, right));
}
};
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return subTree(nums, 0, nums.size() - 1);
}
TreeNode* subTree(vector<int>& nums, int left, int right)
{
if (left > right) {
return nullptr;
}
// 为保证父节点出发,都是平衡二叉搜索树,即左右子节点的高度差<=1,故必须每次用[left, right]的中间mid并所在位置的值作为结点值
int mid = left + (right - left + 1) / 2;
return new TreeNode(nums[mid], subTree(nums, left, mid - 1), subTree(nums, mid + 1, right));
}
};
第109题 有序链表转换为二叉搜索树
递归 / DFS:
两种写法,与 “有序数组->二叉搜索树” 写法相似。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
if (head == nullptr)
{
return nullptr;
}
// len = 链表的长度-1,即最后一个非空节点的索引
for (ListNode* tmp = head, int len = 0; tmp->next != nullptr; tmp = tmp->next)
{
++len;
}
return subTree(head, 0, len);;
}
TreeNode* subTree(ListNode* head, int start, int end)
{
if (start > end)
{
return nullptr;
}
int mid = start + (end - start + 1) / 2;
ListNode* tmp = head;
for (int cnt = 0; cnt != mid; ++cnt)
{
tmp = tmp->next;
}
return (new TreeNode(tmp->val, subTree(head, start, mid - 1), subTree(head, mid + 1, end)));
}
};
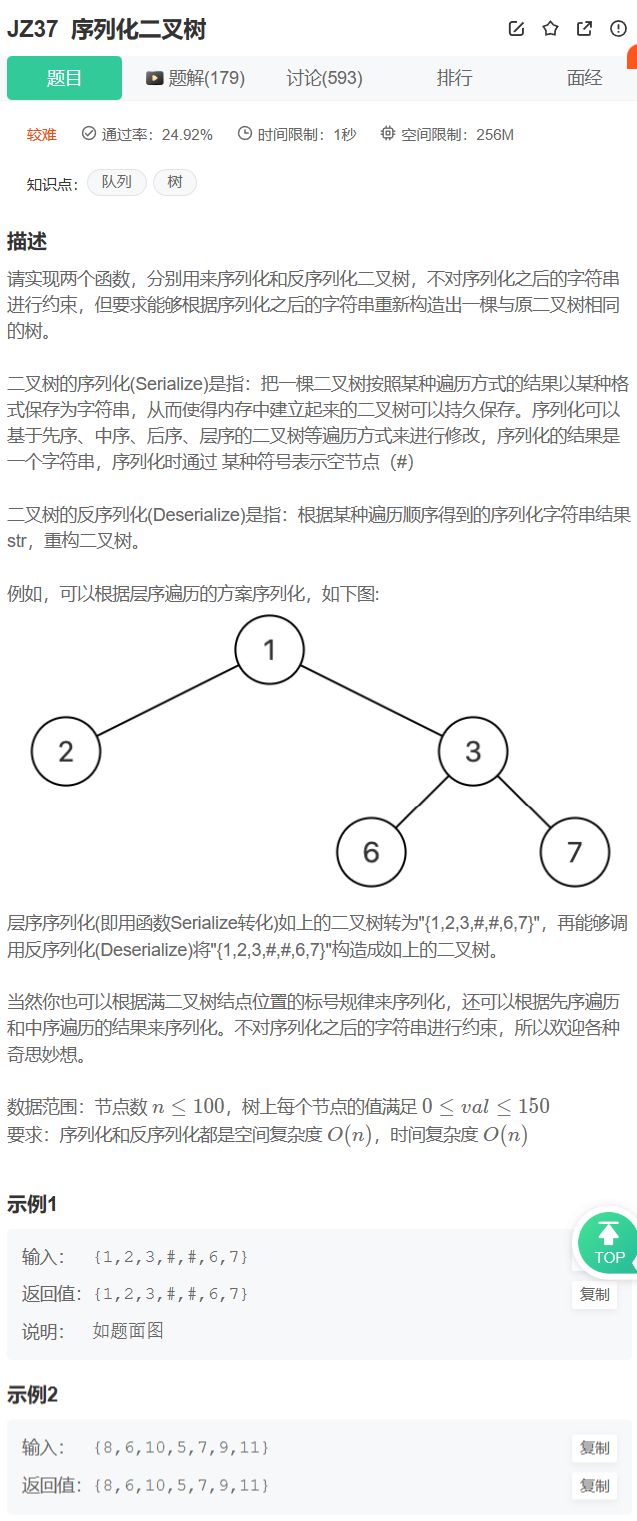
序列化二叉树:
前序序列 <–> 二叉树:
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
// 序列化可以基于先序、中序、后序、层序的二叉树等遍历方式来进行修改,这里选择最简单的先序遍历完成序列化和反序列化。
class Solution {
private:
void preorder(TreeNode *root, string& ret){
if(root == nullptr) // 若为空节点用'#'表示
{
ret += "#";
return;
}
ret += to_string(root->val) + ",";
preorder(root->left, ret);
preorder(root->right, ret);
}
public:
char* Serialize(TreeNode *root) {
string ret;
preorder(root, ret);
// string --> char*
char* ans = new char[ret.size() + 1];
strcpy(ans, ret.c_str());
return ans;
}
private:
TreeNode* deserialize(char *str, int& p) {
if(str[p] == '#')
{
++p;
return nullptr;
}
bool sign = true; // sign标志当前结点的正负
if(str[p] == '-')
{
sign = false;
++p;
}
int val = 0; // 当前结点的绝对值
while(str[p] != ',')
{
val = val * 10 + (str[p] - '0');
++p;
}
if(!sign)
{
val = 0 - val;
}
++p; // 此时str[p] == ',',故要向后再走一步
TreeNode* root = new TreeNode(val);
root->left = deserialize(str, p);
root->right = deserialize(str, p);
return root;
}
public:
TreeNode* Deserialize(char *str) {
int p = 0; // 指向str中待处理的位置
return deserialize(str, p);
}
};
层序序列 <–> 二叉树:
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
// 序列化可以基于先序、中序、后序、层序的二叉树等遍历方式来进行修改,这里选择层序遍历完成序列化和反序列化。
class Solution {
public:
char* Serialize(TreeNode *root) {
if (root == nullptr)
{
return nullptr;
}
string result = "";
levelOrderRecursive(root, result);
// 本质上,通过拷贝完成,const char* ==> char* 的转换
char* ret = new char[result.size() + 1]; // 分配内存空间
strcpy(ret, result.c_str());
return ret;
}
private:
void levelOrderRecursive(TreeNode* root, string& result)
{
queue<TreeNode*> level;
level.push(root); result += (to_string(root->val) + ",");
while (!level.empty())
{
TreeNode* tmp = level.front(); level.pop();
if (tmp->left != nullptr) {
level.push(tmp->left);
result += (to_string(tmp->left->val) + ",");
} else {
result += ("#");
}
if (tmp->right != nullptr) {
level.push(tmp->right);
result += (to_string(tmp->right->val) + ",");
} else {
result += ("#");
}
}
}
public:
TreeNode* Deserialize(char *str) {
if(!str)
{
return nullptr;
}
// 将str中的'#'和具体的节点数据"val",保存在vector中
string data = string(str);
vector<string> nodeVals; // 先对data预处理一下
for(int i = 0; i < data.size(); i++)
{
if(data[i] == '#')
{
nodeVals.push_back(string("#")); // 为空则用"#"表示
}
else
{
int j = i;
while(data[j] != ',')
{
++j;
}
nodeVals.push_back(data.substr(i, j - i)); // 不为空则用"val"表示
i = j;
}
}
// 用层序遍历的方式,取出nodeVals中节点的值,用来构建整个二叉树上
// stoi()函数可以将string转换为int
TreeNode* root = new TreeNode(stoi(nodeVals[0])); // 创建根节点
queue<TreeNode*> nodes;
nodes.push(root); // 根节点入队
for (int k = 1; k < nodeVals.size(); k += 2)
{
TreeNode* tmp = nodes.front(); nodes.pop();
TreeNode *l = nullptr, *r = nullptr;
if(nodeVals[k] != "#")
{
l = new TreeNode(stoi(nodeVals[k]));
nodes.push(l);
}
tmp->left = l;
if(nodeVals[k + 1] != "#")
{
r = new TreeNode(stoi(nodeVals[k + 1]));
nodes.push(r);
}
tmp->right = r;
}
return root;
}
};
第104题 二叉树的最大深度
DFS(有返回值):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// DFS:
int maxDepth(TreeNode* root) {
if (root == nullptr)
{
return 0;
}
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
BFS:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// BFS:
int maxDepth(TreeNode* root) {
if (root == nullptr)
{
return 0;
}
int depth = 0;
queue<TreeNode*> traverseLevelOrder; traverseLevelOrder.push(root);
while (!traverseLevelOrder.empty())
{
queue<TreeNode*> traverseLevelOrder_tmp;
while (!traverseLevelOrder.empty())
{
TreeNode* node = traverseLevelOrder.front(); traverseLevelOrder.pop();
if (node->left != nullptr)
{
traverseLevelOrder_tmp.push(node->left);
}
if (node->right != nullptr)
{
traverseLevelOrder_tmp.push(node->right);
}
}
++depth;
traverseLevelOrder = traverseLevelOrder_tmp;
}
return depth;
}
};
第111题 二叉树的最小深度
BFS:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// BFS,借助队列实现:
int minDepth(TreeNode* root) {
int depth = 0;
if (root == nullptr)
{
return depth;
}
queue<pair<int, TreeNode*>> BFSProcess; // pair表示value所在的结点的key层数
BFSProcess.push({1, root});
while (!BFSProcess.empty())
{
pair<int, TreeNode*> node = BFSProcess.front(); BFSProcess.pop();
// 如果node结点的两个左右子结点都为nullptr,则node为叶子节点
if ((node.second)->left == nullptr && (node.second)->right == nullptr)
{
depth = node.first;
break;
}
if ((node.second)->left != nullptr)
{
BFSProcess.push({node.first + 1, (node.second)->left});
}
if ((node.second)->right != nullptr)
{
BFSProcess.push({node.first + 1, (node.second)->right});
}
}
return depth;
}
};
_DFS:
class Solution {
public:
// DFS:
int minDepth(TreeNode* root) {
int depth = 0;
if (root == nullptr)
{
return depth;
}
int left_minDepth = minDepth(root->left);
int right_minDepth = minDepth(root->right);
/*
如果root结点两个子结点,则从root结点向叶子节点时的最小深度是min(left_minDepth, right_minDepth) + 1
如果root结点只有一个子结点,则从root结点向叶子节点时的最小深度是left_minDepth + right_minDepth + 1 = left_minDepth 或 right_minDepth + 1
如果root结点只有一个子结点,则从root结点向叶子节点时的最小深度是left_minDepth + right_minDepth + 1 = 1
*/
return (root->left == nullptr || root->right == nullptr) ? left_minDepth + right_minDepth + 1 : min(left_minDepth, right_minDepth) + 1;
}
};
第101题 对称二叉树
递归/DFS(有返回值):
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
bool isSymmety;
public:
bool isSymmetric(TreeNode* root) {
this->isSymmety = true;
DFS(root->left, root->right);
return isSymmety;
}
void DFS(TreeNode* root1, TreeNode* root2)
{
if (root1 == nullptr && root2 == nullptr)
{
return;
}
else if ((root1 != nullptr && root2 == nullptr) || (root1 == nullptr && root2 != nullptr))
{
isSymmety = false;
return;
}
DFS(root1->left, root2->right);
if (root1->val != root2->val)
{
isSymmety = false;
return;
}
DFS(root1->right, root2->left);
}
};
/* 角度二: */
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return DFS(root, root);
}
private:
bool DFS(TreeNode* root1, TreeNode* root2)
{
if (root1 == nullptr && root2 != nullptr || root1 != nullptr && root2 == nullptr)
{
return false;
}
if (root1 == nullptr && root2 == nullptr)
{
return true;
}
return (root1->val == root2->val && DFS(root1->left, root2->right) && DFS(root1->right, root2->left));
}
};
迭代BFS+队列:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
bool isSymmety;
public:
bool isSymmetric(TreeNode* root) {
this->isSymmety = true;
queue<TreeNode*> root_left; queue<TreeNode*> root_right;
root_left.push(root->left); root_right.push(root->right);
while (!root_left.empty() || !root_right.empty())
{
if ((!root_left.empty() && root_right.empty()) && (root_left.empty() && !root_right.empty()))
{
return false;
}
TreeNode* node1 = root_left.front(); root_left.pop();
TreeNode* node2 = root_right.front(); root_right.pop();
if ((node1 != nullptr && node2 == nullptr) || (node1 == nullptr && node2 != nullptr))
{
return false;
}
else if (node1 == nullptr && node2 == nullptr)
{
continue;
}
else
{
if (node1->val == node2->val)
{
root_left.push(node1->left); root_left.push(node1->right);
root_right.push(node2->right); root_right.push(node2->left);
}
else
{
return false;
}
}
}
return true;
}
};
第100题 相同的树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == nullptr && q == nullptr)
{
return true;
}
if ((p == nullptr && q != nullptr) || (p != nullptr && q == nullptr))
{
return false;
}
return ((p->val == q->val) && isSameTree(p->left, q->left) && isSameTree(p->right, q->right));
}
};
二叉树的镜像:
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
* @return TreeNode类
*/
TreeNode* Mirror(TreeNode* pRoot) {
if (pRoot == nullptr)
{
return nullptr;
}
pRoot->left = Mirror(pRoot->left);
pRoot->right = Mirror(pRoot->right);
swap(pRoot->left, pRoot->right);
return pRoot;
}
};
二叉树的下一个节点
/*
struct TreeLinkNode {
int val;
struct TreeLinkNode *left;
struct TreeLinkNode *right;
struct TreeLinkNode *next;
TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {
}
};
*/
class Solution {
public:
// 返回中序序列中,pNode的下一个节点
TreeLinkNode* GetNext(TreeLinkNode* pNode) {
// pNode存在右子树
if (pNode->right != nullptr)
{
// 只需找到右子树中最左下的节点
TreeLinkNode* rightRoot = pNode->right;
while (rightRoot->left != nullptr)
{
rightRoot = rightRoot->left;
}
return rightRoot;
}
// pNode不存在右子树
// 1. 当前节点为其父节点的左子节点,故只需返回pNode的父节点即可
if (pNode->next != nullptr && pNode->next->left == pNode)
{
return pNode->next;
}
// 2. 当前节点为其父节点的右子节点
if (pNode->next != nullptr && pNode->next->right == pNode)
{
// pNode向左上不断移动,直到parentNode所处节点的父节点为根节点
TreeLinkNode* parentNode = pNode->next;
while (parentNode->next != nullptr && parentNode->next->right == parentNode)
{
parentNode = parentNode->next;
}
return parentNode->next;
}
return nullptr;
}
};
二叉树的镜像
第226题 翻转二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == nullptr)
{
return nullptr;
}
TreeNode* tmp = root->left;
root->left = invertTree(root->right);
root->right = invertTree(tmp);
return root;
}
};
第951题 翻转等价二叉树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool flipEquiv(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr && root2 == nullptr)
{
return true;
}
if (root1 == nullptr || root2 == nullptr || (root1->val != root2->val))
{
return false;
}
return (flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right)) || (flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left));
}
};
第236题 二叉树的最近公共祖先
找到根节点到p、q的两条路径,并得到其交点:
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
// 哈希表中保存了每个节点的直接父节点
unordered_map<int, TreeNode*> nodeParent;
void DFS(TreeNode* root)
{
if (root == nullptr)
{
return;
}
if (root->left != nullptr)
{
nodeParent[root->left->val] = root;
DFS(root->left);
}
if (root->right != nullptr)
{
nodeParent[root->right->val] = root;
DFS(root->right);
}
}
private:
unordered_set<int> visited;
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 将所有结点和其对应的父节点存放在哈希表中
if (root != nullptr)
{
// 根节点的父节点为nullptr
nodeParent[root->val] = nullptr;
}
DFS(root);
// 从哈希表中,不断地从p和q开始分别向上找,最后相当于找到两个路径(根节点到p和q地两条路径),故找到该两条路径存在地交点即可
//,具体实现时,先不断地向上找p的父节点直到最后父节点为空;之后,从q开始向上找,如果出现了与p找到的路径有交点,则返回交点即可
while (p != nullptr)
{
visited.insert(p->val);
p = nodeParent[p->val];
}
while (q != nullptr)
{
if (visited.count(q->val))
{
return q;
}
q = nodeParent[q->val];
}
return nullptr;
}
};
递归:(不太理解)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
TreeNode* lca;
bool DFS(TreeNode* root, TreeNode* p, TreeNode* q)
{
if (root == nullptr)
{
return false;
}
// leftSubTree表示root结点的左子树是否包含p或q
// rightSubTree表示root结点的右子树是否包含p或q
bool leftSubTree = DFS(root->left, p, q);
bool rightSubTree = DFS(root->right, p, q);
// root结点是p,q的公共祖先 || root结点就是p或者q,且root结点左右子树中含有q或p
if ((leftSubTree && rightSubTree) || ((leftSubTree || rightSubTree) && (root->val == p->val || root->val == q->val)))
{
lca = root;
}
return leftSubTree || rightSubTree || (root->val == p->val || root->val == q->val);
}
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
DFS(root, p, q);
return lca;
}
};