三篇论文联合复现：高比例新能源下考虑需求侧响应和智能软开关的配电网重构程序代码！

适用平台：Matlab+Yalmip+Cplex

程序在高比例新能源接入的情况下提出了考虑需求响应（DR）和智能软开关（SOP）的多时段主动配电网重构策略，进一步降低配电系统重构费用，减少弃风率和弃光率；基于混合整数二阶锥规划对配电网重构模型进行求解，将模型转化为MISOCP问题，并在调用CPLEX求解器进行求解。程序中算例丰富、注释清晰、干货满满，可扩展性和创新性很高！下面对文章和程序做简要介绍！

程序创新点：

1）配电网重构; 2）高比例可再生能源；

3）需求响应DR；4）智能软开关SOP。

主要工作：

程序提出了高比例新能源接入下考虑需求侧响应(DR)和智能软开关(SOP)的配电网重构策略。首先，构建了配电网重构下的DR和SOP模型；然后，综合考虑网损费用、弃风费用、弃光费用和开关费用，以社会利益最大化为优化目标，构建高比例新能源接入下多时段配电网重构模型；再次，通过大M法和二阶锥松弛将配电网重构模型转化为混合整数二阶锥规划问题，并采用Matlab调用YALMIP和CPLEX对转化后的模型进行求解；最后，采用改进的IEEE33节点配电系统进行了算例仿真，并进行了灵敏度分析和不同配电网重构策略的对比分析，验证了模型的有效性。所提考虑DR和SOP的配电网重构策略，可以有效提高配电系统的新能源消纳能力，平抑负荷峰谷差，提升配电网运行的经济性。

（1）智能软开关（SOP）

智能软开关(soft open point , SOP)是一种电力电子装置,用于替代传统联络开关,能有效解决配电系统中功率调节能力不足的问题。SOP可在馈线之间实现快速、动态和持续的有功无功潮流控制,起到平衡负载潮流并优化系统电压分布的作用。SOP的应用提高了配电网潮流的可控性,可有效解决高渗透率DG接入配电网带来的一系列问题,从而改善系统运行的经济性、灵活性和可靠性。

（2）需求响应

DR是指电力用户根据价格信号或激励机制做出响应，以此改变用户的常规电力消费行为。DR往往采用峰谷电价的形式引导用户的用电行为，从而将高峰时段的部分负荷转移到低谷时段，达到削峰填谷、平衡负荷的目的。政府制定的峰谷电价是一个长效机制，考虑到电价政策的调控变动在中国实施的难度，针对用户电价体系中的分时电价，现阶段已有一些研究工作通过积分制和电价套餐的方式来实现。

（3）Distflow潮流约束

dist-flow 潮流方程是基于Kirchhoff电流定律和Kirchhoff电压定律建立的。它考虑了配电系统中各节点之间的阻抗和功率负荷，通过求解一组非线性方程，得到各节点的电压和功率的分布情况，在dist-flow潮流方程中，首先需要确定各节点的电压幅值和相角，然后，根据节点电压和阻抗，计算节点注入功率和节点注入电流根据Kirchhoff电流定律和Kirchhoff电压定律，可以得到一组非线性方程。通过求解这组非线性方程，可以得到各节点的电压和功率的分布情况。相比于传统的基于节点功率的潮流计算法，Distflow 潮流模型更适用于辐射状配电系统的潮流计算。

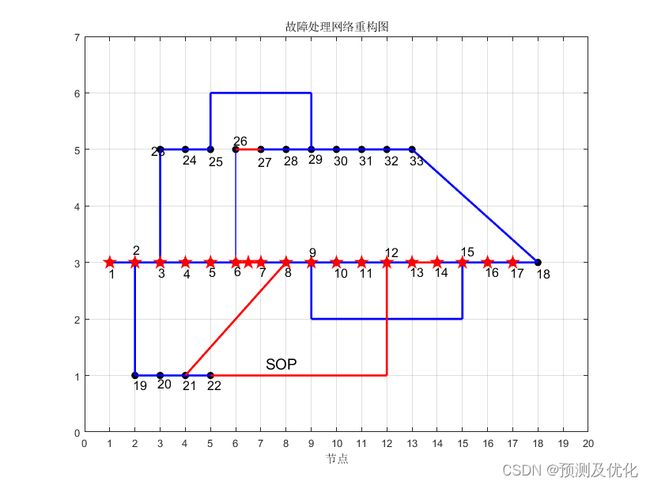
程序结果：

部分程序：

delta_T=1;  N=1;S_sopi1=1;    S_sopj1=1;%SOP容量 
nl=37;nc=5;%37条线 5条联络线
xb=[33 12 22 0.1 0.1;34 8 21 0.1 0.1;35 15 9 0.1 0.1;36 25 29 0.1 0.1;37 18 33 0.1 0.1];%联络线的Branch矩阵
Branch=[Branch;xb];r_ij=Branch(:,4);   x_ij=Branch(:,5);
p_Solar=zeros(33,1);p_Wind=zeros(33,1);p_Load=p_load;
p_Solar(5)=0.05;p_Solar(11)=0.05;p_Solar(15)=0.05;p_Solar(22)=0.05;p_Solar(31)=0.05;%分布式功率  
q_Solar=p_Solar.*0.05;%无功按照有功的0.05倍 
lamda=sdpvar(33,N,'full');
x_Iij_square=sdpvar(37,N,'full');   x_ui_square=sdpvar(33,N,'full');
x_pij=sdpvar(37,N,'full');      x_qij=sdpvar(37,N,'full');
x_p_sop1=sdpvar(2,N,'full');    x_q_sop1=sdpvar(2,N,'full');
opt_num=1;beta=binvar(37,37,'full');Zij=binvar(nl,1);%网架结构
Z0=[ones(nl-nc,1);zeros(nc,1)];%初始拓扑 32条全连接 5条断开
assign(Zij,Z0);%为Zij与Z0赋初始值x_sop_L=sdpvar(2,N,'full');%sop损失
Constraints=[];%for opt_num=1:N    
Constraints = [Constraints, sum(Zij) == 32];%网架结构
Constraints = [Constraints, 0<= x_pij(33:37) <= 0.1.*Zij(33:37)];
Constraints=[Constraints,
    implies(Zij(i)==0,[beta(Branch(i,2),Branch(i,3))==0,beta(Branch(i,3),Branch(i,2))==0]),%非联通情况下的参数关系
    implies(Zij(i)==1,[beta(Branch(i,2),Branch(i,3))+beta(Branch(i,3),Branch(i,2))==1])];%联通情况下的参数关系
        if ~ismember([i,j],Branch(:,[2,3]))
Constraints=[Constraints,beta(i,j)==0];%非联通节点的参数beta设置为0
Constraints=[Constraints,sum(beta(1:37,:),2)==1];%公式6c
Constraints=[Constraints,beta(1,2)==0];%6d
%% 定义目标函数
  f=r_ij'*x_Iij_square(:,opt_num)+100*sum(p_load)+100*sum(-lamda.*p_load);
  Constraints=[Constraints,x_ui_square(1,opt_num)==12.66^2];
  Constraints=[Constraints,0<=lamda<=1];
% Constraints=[Constraints,x_Iij_square(7,opt_num)==0];%设置故障线路1
  Constraints=[Constraints,Zij(6)==0];Constraints=[Constraints,Zij(35)==0];

欢迎感兴趣的小伙伴关注，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！