数据结构之图的定义与存储

  数据结构是程序设计的重要基础，它所讨论的内容和技术对从事软件项目的开发有重要作用。学习数据结构要达到的目标是学会从问题出发，分析和研究计算机加工的数据的特性，以便为应用所涉及的数据选择适当的逻辑结构、存储结构及其相应的操作方法，为提高利用计算机解决问题的效率服务。
  数据结构是指数据元素的集合及元素间的相互关系和构造方法。元素之间的相互关系是数据的 逻辑结构，数据元素及元素之间关系的存储称为 存储结构(或物理结构)。数据结构按照逻辑关系的不同分为 线性结构和 非线性结构两大类，其中，非线性结构又可分为树结构和图结构。
  图是比树结构更复杂的一种数据结构。在线性结构中，除首结点没有前驱、末尾结点没有后继外，一个结点只有唯一的一个直接前驱和唯一的一个直接后继。在树结构中，除根结点没有前驱结点外，其余的每个结点只有唯一的一个前驱(双亲) 结点和多个后继 (子树) 结点。而在图中，任意两个结点之间都可能有直接的关系，所以图中一个结点的前驱结点和后继结点的数目是没有限制的。

1、图的定义

  图G 是由集合V和E构成的二元组，记作 G=(V,E)，其中，V是图中顶点的非空有限集合，E 是图中边的有限集合。从数据结构的逻辑关系角度来看，图中任一顶点都有可能与其他顶点有关系，而图中所有顶点都有可能与某一顶点有关系。在图中，数据元素用顶点表示，数据元素之间的关系用边表示。
  （1）有向图。若图中每条边都是有方向的，那么顶点之间的关系用i,v_j>表示，它说明从v_i到v_j有一条有向边(也称为弧)。v_i是有向边的起点，称为弧尾；v_j是有向边的终点，称为弧头。所有边都有方向的图称为有向图。
  （2）无向图。若图中的每条边都是无方向的，顶点 v_i和v_j之间的边用(v_i,v_j)表示。因此，在有向图中i,v_j>与j,v_i>分别表示两条边，而在无向图中(v_i,v_j) 与(v_j,v_i)表示的是同条边。
  （3）完全图。若一个无向图具有 n 个顶点，而每一个顶点与其他 n-1 个顶点之间都有边，则称之为无向完全图。显然，含有 n 个顶点的无向完全图共有$\frac{n(n-1)}{2}$条边。类似地，有n个顶点的有向完全图中弧的数目为 n(n-1)，即任意两个不同顶点之间都有方向相反的两条弧存在。
  （4）度、出度和入度。顶点v的度是指关联于该顶点的边的数目，记作 D(v)。若 G 为有向图，顶点的度表示该顶点的入度和出度之和。顶点的入度是以该顶点为终点的有向边的数目，而顶点的出度指以该顶点为起点的有向边的数目，分别记为 ID(v)和 OD(v)。无论是有向图还无向图，顶点数n、边数 e与各顶点的度之间有以下关系
$$e=\frac{1}{2}{\Sigma }_{i=1}^{n}D(v_i)$$
  （5）路径。在无向图 G 中，从顶点v_p到顶点v_q 的路是指在一个顶点序列 v_p，v_i1，v_i2，···，v_in，v_q，使得(v_p，v_i1)，(v_i1， v_i2)，···，(v_in，v_q)均属于 E(G)。若G 是有向图，其路径也是有方向的，它由 E(G)中的有向边p，v_i1>，i1， v_i2>，···，in，v_q>组成。路径长度是路径上边或弧的数目。第一个顶点和最后一个顶点相同的路径称为回路或环。若一条路径上除了v_p和v_q可以相同外，其余顶点均不相同，则称其为简单路径。
  （6）子图。若有两个图 G=(V，E) 和 G’=(V’，E’)，如果 V’⊆V 且 E’⊆E，则称G’为G的子图。
  （7）连通图与连通分量。在无向图 G 中，若从项点 v_i 到项点 v_j 有路径，则称顶点和顶点是连通的。如果无向图 G 中任意两个顶点都是连通的，则称其为连通图。无向图 G 的极大连通子图称为 G的连通分量。
  （8）强连通图与强连通分量。在有向图 G 中，如果对于每一对顶点 v_i，v_j∈V 且 v_i≠v_j， 从顶点v_i到顶点v_j 和从顶点 v_j 到顶点 v_i 都存在路径，则称图 G 为强连通图。有向图中的极大连通子图称为有向图的强连通分量。
  （9）网。边(或弧) 带权值的图称为网。
  （10）有向树。如果一个有向图恰有一个顶点的入度为 0，其余顶点的入度均为 1，则是棵有向树。
  从图的逻辑结构的定义来看，图中的顶点之间不存在全序关系(即无法将图中的顶点排列成一个线性序列)，任何一个顶点都可被看成第一个顶点；另一方面，任一顶点的邻接点之间也不存在次序关系。为了便于运算，给图中的每个顶点赋予一个序号值。

2、图的存储结构

  图的基本存储结构有邻接矩阵表示法和邻接链表表示法两种。
  （1）邻接矩阵表示法
  图的邻接矩阵表示法是指用一个矩阵来表示图中顶点之间的关系。对于具有n个顶点的图G=(V,E)，其邻接矩阵是一个 n 阶方阵，且满足：
$$A[i][j]={\{}_{0若(v_i,v_j)或<v_i,v_j>不是E中的边}^{1若(v_i,v_j,)或<v_i,v_j>是E中的边}$$
  由邻接矩阵的定义可知，无向图的邻接矩阵是对称的，有向图的邻接矩阵则不一定对称。借助于邻接矩阵容易判定任意两个顶点之间是否有边(或弧)相连，并且容易求得各个顶点的度。对于无向图，顶点 v_i 的度是邻接矩阵第 i 行(或列)中值不为 0的元素个数；对于有向图，第 i 行(或列)中值不为 0的元素个数是顶点 v_i 的出度 OD(v_i)，第 j 列的非0元素个数是顶点v_j 的入度ID(v_j)。
  网（赋权图）的邻接矩阵可定义为:
$$A[i][j]={\{}_{\infty 若(v_i,v_j)或<v_i,v_j>不属于E}^{W_{ij}若(v_i,v_j,)或<v_i,v_j>属于E}$$
其中，W_ij是边(弧) 上的权值。
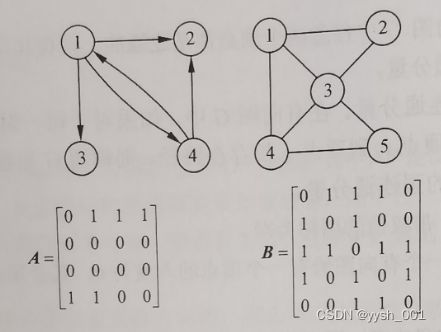
  下图所示的有向图和无向图的邻接矩阵分别为A和B。

  下图 所示的是一个网及其邻接矩阵 C。

  若用邻接矩阵表示图，则对应的数据类型可定义为:

#define MaxN 30							/*图中顶点数目的最大值*/
typedef int AdjMatrix[MaxN][MaxN]:
或
typedef double AdjMatrix[MaxN][MaxN]	/*邻接矩阵*/
typedef struct {
	int Vnum;								/*图中的顶点数目*/
	AdjMatrix Arcs;
}Graph;

  （2）邻接链表表示法
  邻接链表表示法指的是为图的每个顶点建立一个单链表，第i个单链表中的结点表示依附于顶点v_i 的边(对于有向图是以 v_i 为尾的弧)。邻接链表中的结点有表结点(或边结点) 和表头结点两种类型，如下所示。

  其含义如下。
   ● adjvex： 指示与顶点v_i邻接的顶点的序号。
   ● nextarc：指示下一条边或弧的结点。
   ● info： 存储与边或弧有关的信息，如权值等
   ● data： 存储顶点 v_i的名或其他有关信息。
   ● firstarc：指示链表中的第一个结点(邻接顶点)。
  这些表头结点通常以顺序的形式存储，以便随机访问任一顶点的邻接链表。若图用邻接链表来表示，则对应的数据类型可定义如下：

#define MaxN 50					/*图中顶点数目的最大值*/
typedef struct ArcNode{			/*邻接链表的表结点*/
	int adjvex;					/*邻接顶点的顶点序号*/
	double weight;				/*边(弧)上的权值*/
	struct ArcNode *nextarc;	/*指向下一个邻接顶点的指针*/
}EdgeNode;
typedef struct VNode{			/*邻接链表的头结点*/
	char data;					/*顶点表示的数据，以一个字符表示*/
	struct ArcNode *firstarc;	/*指向第一条依附于该顶点的边或弧的指针*/
}AdjList[MaxN];
typedef struct {
	int Vnum;					/*图中顶点的数目*/
	AdjList Vertices;
}Graph;

  显然，对于有 n 个顶点、e 条边的无向图来说，其邻接链表需用 n 个头结点和 2e 个表结点。
  对于无向图的邻接链表，顶点 v_i 的度恰为第 i 个邻接链表中表结点的数目，而在有向图中，为求顶点的入度，必须扫描逐个邻接表，这是因为第 i 个邻接链表中表结点的数目只是顶点 v_i 的出度。为此，可以建立一个有向图的逆邻接链表。有向图的邻接表和逆邻接表如下图所示。