BP网络逼近仿真实例详解

题目

使用BP网络逼近对象
采样时间取1ms。输入信号为u(k) = 0.5sin(6πt)。神经网络为2-6-1结构，权值为W_1，W_2的初始值取[-1,+1]之间的随机值，取η=0.50，α=0.05。

解题思路

我们知道用于逼近的BP网络如下图所示

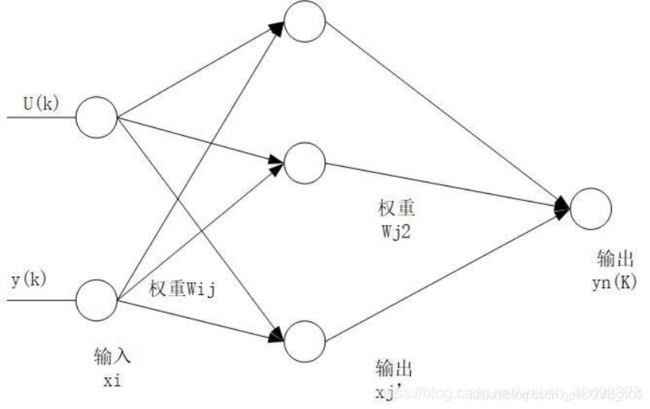
BP网络工作流程也如下图所示

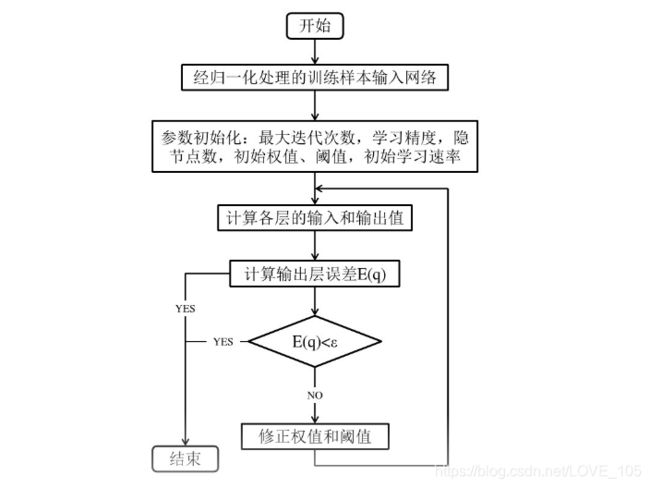
通过这两张图我们可以得到
隐含层神经元的输入即为所有输入信号的加权和

隐含层的输出 x j ′

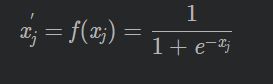
输出层神经元的输出为隐含层输出加权和：

误差为：

准则函数为
Δw_j0(图中的j2应为j0
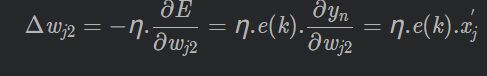Δw_ij

该题的权值修改公式为
w_j0 (k+1)=w_j0 (k) +Δw_j0+α(w_j0 (k)-w_j0 (k-1))
w_ij (k+1)=w_ij (k) +Δw_ij+α(w_ij (k)-w_ij (k-1))

代码

BP网络逼近。

clear all;
close all;
xite = 0.50;
alfa = 0.05;
w2 = rands(6,1);
w2_1 = w2;
w2_2 = w2_1;
w1 = rands(2,6);
w1_1 = w1;
w1_2 = w1;
dw1 = 0 * w1;
x = [0,0]';
u_1 = 0;
y_1 = 0;
I = [0,0,0,0,0,0]';
Iout = [0,0,0,0,0,0]';
FI = [0,0,0,0,0,0]';
ts = 0.001;
for k = 1:1:1000
    time(k) = k*ts;
    u(k) = 0.5*sin(6*pi*ts*k);
    y(k) = u_1^3 + y_1/(1+y_1^2);
    for j = 1:1:6
        I(j) = x' * w1(:,j);
        Iout(j) = 1/(1+exp(-I(j)));
    end
    yn(k) = w2' * Iout;
    e(k) = y(k) - yn(k);
    w2 = w2_1 + (xite*e(k))* Iout + alfa *(w2_1 - w2_2);
    for j = 1:1:6
        FI(j) = exp(-I(j))/(1+exp(-I(j)))^2;
    end
    for i = 1:1:2
        for j = 1:1:6
            dw1(i,j) = e(k) * xite * FI(j) * w2(j) *x(i);
        end
    end
    w1 = w1_1 + dw1 +alfa * (w1_1 - w1_2);
    yu = 0;
    for j = 1:1:6
        yu = yu + w2(j) * w1(1,j) * FI(j);
    end
    dyu(k) = yu;
    x(1) = u(k);
    x(2) = y(k);
    w1_2 = w1_1;
    w1_1 = w1;
    w2_2 = w2_1;
    w2_1 = w2;
    u_1 = u(k);
    y_1 = y(k);
end
figure(1);
plot(time,y,'r',time,yn,'b');
xlabel('times');ylabel('y and yn');
figure(2);
plot(time,y-yn,'r');
xlabel('times');ylabel('error');
figure(3);
plot(time,dyu);
xlabel('times');ylabel('dyu');

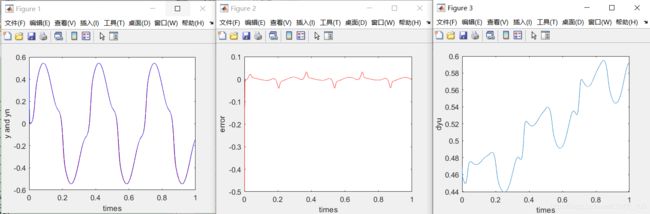
运行结果

代码详解

首先是确定初始W_1,W_2,得到权值，
我们知道被控对象是实际输出，而u(k),y(k)则是输入，因为知道了u(k)则我们也就可以得到实际输出y(k)。
之后就是根据公式进行计算了。
隐含层的输出 x j ′

  for j = 1:1:6
        I(j) = x' * w1(:,j);
        Iout(j) = 1/(1+exp(-I(j)));
  end

输出层神经元的输出

  yn(k) = w2' * Iout;

误差

   e(k) = y(k) - yn(k);

w_j0 (k+1)和w_ij (k+1)′

   w2 = w2_1 + (xite*e(k))* Iout + alfa *(w2_1 - w2_2);
   for j = 1:1:6
        FI(j) = exp(-I(j))/(1+exp(-I(j)))^2;
    end
    for i = 1:1:2
        for j = 1:1:6
            dw1(i,j) = e(k) * xite * FI(j) * w2(j) *x(i);
        end
    end
    w1 = w1_1 + dw1 +alfa * (w1_1 - w1_2);

y_n

    for j = 1:1:6
        yu = yu + w2(j) * w1(1,j) * FI(j);
    end

通过不断调整权值得到比较好的理想输出函数。