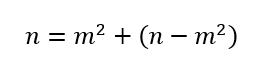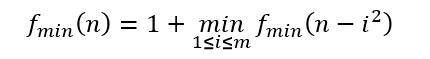- 【LeetCode 热题100】 23. 合并 K 个升序链表的算法思路及python代码
pljnb
LeetCode热题100算法leetcode链表
23.合并K个升序链表给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。示例1:输入:lists=[[1,4,5],[1,3,4],[2,6]]输出:[1,1,2,3,4,4,5,6]解释:链表数组如下:[1->4->5,1->3->4,2->6]将它们合并到一个有序链表中得到。1->1->2->3->4->4->5->6示例2:输入:lists=[
- 【Leetcode刷题随笔】59 螺旋矩阵
Poor_DayDreamer
leetcode数组篇MediumTagleetcode矩阵算法
1.题目描述给定一个正整数n,生成一个包含1到n2所有元素,且元素按顺时针顺序螺旋排列的nxn正方形矩阵matrix。可结合以下原题链接阅读。原题链接:59螺旋矩阵2.解题思路本题为模拟矩阵填充过程,不需要设计算法,只要完成正确的填充过程即可。首先初始化一个nxn的二维矩阵(涉及到动态内存分配),从矩阵左上角开始往顺时针填充,关键在于填充的转角处不要重复填充,所以对于每条边都要遵循严格的统一规则,
- 【Leetcode刷题随笔】203移除链表元素
Poor_DayDreamer
leetcode链表篇leetcode链表算法
1.题目描述题意:删除链表中等于给定值val的所有节点。示例1:输入:head=[1,2,6,3,4,5,6],val=6输出:[1,2,3,4,5]示例2:输入:head=[],val=1输出:[]示例3:输入:head=[7,7,7,7],val=7输出:[]原题链接:203移除链表元素2.解题思路由于链表本身的性质,移除链表的某个节点a,只需要将前一个节点的next指针指向a的下一个节点即可
- 【Leetcode刷题随笔】844 比较含退格的字符串
Poor_DayDreamer
移除元素篇字符串篇leetcode算法职场和发展
1.题目描述给定s和t两个字符串,比较s和t是否在删除所有由#字符表示的退格操作后相等。退格操作会删除其前面(不包括#本身)的一个字符,如果前面没有字符则忽略该#。如果字符串的末尾有多个退格符,它们会相互抵消,直到没有退格符剩余或者所有字符都被删除。示例1:输入:s=“ab#c”,t=“ad#c”输出:true解释:s和t都会变成“ac”,因为#前面的b和d都被删除。示例2:输入:s=“ab##”
- 【Leetcode刷题随笔】2765最长交替子数组
Poor_DayDreamer
leetcode数组篇leetcode算法职场和发展
1.题目描述:该题目标是在一个整数数组nums中寻找最长的“交替子数组”。这种交替子数组的特点是:其元素按照“递增1,递减1,递增1…”的模式循环排列,且子数组的长度必须大于1,例如数组nums=[2,3,4,3,4],交替子数组有[2,3],[3,4],[3,4,3]和[3,4,3,4]。最长的子数组为[3,4,3,4],长度为4。详细题目描述见原题:原题。2.1解题思路一(双层循环):这道题有
- LeetCode刷题笔记
小李李李李腊八
leetcode算法java
leetcode_01两数之和斐波那契数列三个数最大乘积反转链表x的平方根环形列表LeetCode随笔两数之和给定一个整数数组nums和一个整数目标值target,请你在该数组中找出和为目标值target的那两个整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。暴力法记录下数组第一个数值,对数组进行循环,将之后的值
- 高频SQL50题 第一天 | 1757. 可回收且低脂的产品、584. 寻找用户推荐人、595. 大的国家、1683. 无效的推文、1148. 文章浏览 I
榛果咖啡有点苦
高频SQL50题mysql
1757.可回收且低脂的产品题目链接:https://leetcode.cn/problems/recyclable-and-low-fat-products/description/?envType=study-plan-v2&envId=sql-free-50状态:已完成考点:无selectproduct_idfromProductswherelow_fats='Y'andrecyclable
- 动态规划问题
慕雪_mx
动态规划算法数据结构
动态规划问题最长回文子串题目:给你一个字符串s,找到s中最长的回文子串,并输出.(leetcode5)示例1:输入:s="babad"输出:"bab"解释:"aba"同样是符合题意的答案。示例2:输入:s="cbbd"输出:"bb"代码实现:char*longestPalindrome(char*s){intn=strlen(s);if(n=n)break;if(s[i]!=s[j]){dp[i]
- 动态规划算法优化在资源分配问题中的应用
suyang199312
课程设计
摘要资源分配问题广泛存在于各类生产与管理场景,合理分配资源以实现效益最大化至关重要。本文深入剖析动态规划算法在资源分配问题中的应用,详细阐述其基本原理与常规解法,针对常规解法的不足提出创新优化思路,并给出具体实现步骤。通过实际案例分析与实验验证,展示优化后的动态规划算法在提升资源分配效率和效益方面的显著优势,为相关领域的决策制定提供有力支持。引言在经济、工程、计算机科学等众多领域,资源分配问题无处
- LeetCode 热题 100_跳跃游戏(78_55_中等_C++)(贪心算法)
Dream it possible!
LeetCode热题100leetcodec++贪心算法算法
LeetCode热题100_跳跃游戏(78_55)题目描述:输入输出样例:题解:解题思路:思路一(贪心算法):代码实现代码实现(思路一(贪心算法)):以思路一为例进行调试题目描述:给你一个非负整数数组nums,你最初位于数组的第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标,如果可以,返回true;否则,返回false。输入输出样例:示例1:输入:num
- leetcode501-二叉搜索树中的众数
记得早睡~
算法小课堂leetcode算法javascript数据结构
leetcode501思路由于是二叉搜索树,那么我们知道它的特性:使用中序遍历得到的是从小到大排序的,所以我们利用这个规则,使用count来统计每次出现一个新的数的总个数,maxCount统计最大的个数值,result来存储二叉树中的众数,也就是要得到的结果值,pre用于统计前一个节点值初始化定义好值以后,我们需要使用中序遍历,中间处理逻辑值当pre还不存在的时候或者前一个节点跟后一个节点不相同时
- leetcode530-二叉搜索树的最小绝对值
记得早睡~
算法小课堂leetcodetypescriptjavascript算法数据结构
leetcode530思路这里题目有确切说明这个二叉树是:二叉搜索树那么我们可以想到二叉搜索树的特性,利用中序遍历:左中右得到的结果是从小到达排列的所以我们就只需要计算出每一个节点和前一个节点之间的差值,然后保存最小的差值就是本题答案所以我们在中序遍历的过程中需要存储最小的差值,我们首先初始化result为无穷大,还需要存储前一个节点,用于进行比较,每次遍历到一个节点的时候,我们比较resul和r
- LeetCode98-验证二叉搜索树
学习的学习者
LeetCodePython二叉搜索树
上个星期和导师去了华农一趟名义上是和导师去参加一个国家级的项目其实没我啥事都是我导师在那口若悬河当时和那边的本科生去了另一间会议室交流了关于GAN的知识偶然听说大家都在用pytorch好像最新版的也挺好用的反正就是学术界目前主要用这个框架工业界主要用Tensorflow(没办法,Google出品)这两天也拿来瞧了瞧好像也确实可以的!!!98-验证二叉搜索树给定一个二叉树,判断其是否是一个有效的二叉
- LeetCode第89题_格雷编码
@蓝莓果粒茶
算法leetcode算法职场和发展c++pythonunity游戏程序
LeetCode第89题:格雷编码题目描述n位格雷码序列是一个由2^n个整数组成的序列,其中:每个整数都在范围[0,2^n-1]内(含0和2^n-1)第一个整数是0一个整数在序列中出现不超过一次每对相邻整数的二进制表示恰好一位不同,且第一个和最后一个整数的二进制表示恰好一位不同给你一个整数n,返回任一有效的n位格雷码序列。难度中等问题链接格雷编码示例示例1:输入:n=2输出:[0,1,3,2]解释
- 动态规划 43. 最长回文子序列
Mophead_Zarathustra
小白的代码随想录刷题笔记Mophead的小白刷题笔记leetcodepython代码随想录动态规划
动态规划43.最长回文子序列516.最长回文子序列-力扣(LeetCode)代码随想录难度5-中等太难了,依然不会做。看完题解只觉得恍然大悟原来如此,但是不看直接做就感觉定义和递推就跟挤牙膏一样挤不出,挤出来了也不一定对。与动态规划42.回文子串-CSDN博客要形成对比注意本题中,子序列的要求是:不一定连续思路:(摘录、修改自代码随想录)dp定义:(重要,因为这道题求的是长度,而不是回文子序列个数
- 力扣SQL题记录(持续)
Dxecozy
leetcodesql
此贴用于个人写SQL题记录,主要是用于记录新的知识和一些个人觉得的难题思路,便于复习目录Leetcode高频SQL50题基本题基本条件筛选多表连接新知识CHAR_LENGTH()函数的使用,用于计算字符长度Leetcode高频SQL50题基本题基本条件筛选1757.可回收且低脂的产品584.寻找用户推荐人595.大的国家1148.文章浏览I多表连接1378.使用唯一标识码替换员工ID新知识CHAR
- 【Leetcode】11. 盛最多水的容器
Leuanghing
leetcode算法python
一、题目描述给定一个长度为n的整数数组height。有n条垂线,第i条线的两个端点是(i,0)和(i,height[i])。找出其中的两条线,使得它们与x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明:你不能倾斜容器。示例1:输入:[1,8,6,2,5,4,8,3,7]输出:49解释:图中垂直线代表输入数组[1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示
- 【Leetcode】12. 整数转罗马数字
Leuanghing
leetcode算法python
一、题目描述七个不同的符号代表罗马数字,其值如下:罗马数字是通过添加从最高到最低的小数位值的转换而形成的。将小数位值转换为罗马数字有以下规则:如果该值不是以4或9开头,请选择可以从输入中减去的最大值的符号,将该符号附加到结果,减去其值,然后将其余部分转换为罗马数字。如果该值以4或9开头,使用减法形式,表示从以下符号中减去一个符号,例如4是5(V)减1(I):IV,9是10(X)减1(I):IX。仅
- LeetCode135☞分糖果
fantasy_4
LeetCode刷题javapythonleetcode贪心算法算法
关联LeetCode题号135本题特点贪心两次遍历,一次正序遍历,只比较左边,左边比右边大的情况i-1i一次倒序遍历,只比较右边的,右边比左边大i+1i本题思路classSolution:defcandy(self,ratings:List[int])->int:candy=[1]*len(ratings)#右大于左foriinrange(1,len(ratings)):ifratings[i]>
- LeetCode134☞加油站
fantasy_4
LeetCode刷题pythonleetcodejava算法贪心算法
关联LeetCode题号134本题特点贪心局部最优解-部分差值如果小于0(消耗大于油站油量)就从下一个加油站开始,因为如果中间有小于0的情况当前站就不可能是始发站,整体最优解-整体差值如果小于0,那么就是不能有始发站本题思路classSolution:defcanCompleteCircuit(self,gas:List[int],cost:List[int])->int:curSum=0tota
- LeetCode56☞合并区间
fantasy_4
LeetCode刷题leetcodepythonjava算法贪心算法
关联LeetCode题号56本题特点贪心本题思路将二维数组排序按照左边界排序。排序后,右边界的大小成为找到局部最大值的关键。由题意合并区间可知,应该取数组的’并集‘,局部最优解推出全局最优解,每次找到局部最大的范围,整体就会合并成一个大区间Python写法defmerge(self,intervals):result=[]iflen(intervals)==0:returnresult#区间集合为
- 【Leetcode】430. 扁平化多级双向链表
海绵波波107
#算法和leetcodeleetcode链表算法
目录一、题目二、思路2.1解题思路2.2代码尝试2.3疑难问题2.4AI复盘三、解法四、收获4.1心得4.2举一反三一、题目二、思路2.1解题思路2.2代码尝试/*//DefinitionforaNode.classNode{public:intval;Node*prev;Node*next;Node*child;};*/classSolution{public:Node*flatten(Node
- 动态规划 31. 股票问题总结(类别解析)
Mophead_Zarathustra
Mophead的小白刷题笔记leetcodepython代码随想录动态规划
动态规划31.股票问题总结(类别解析)股票问题给我做的有一些混乱,因此本总结主要是借助GPT的帮助帮我解决下面的核心问题,也希望能通过这些示例与讲解,帮助各位快速厘清各种“股票问题”的通用DP思路。经典股票问题:动态规划25.买卖股票的最佳时机-CSDN博客动态规划26.买卖股票的最佳时机II-CSDN博客动态规划27.买卖股票的最佳时机III(多状态转换初遇)-CSDN博客动态规划28.买卖股票
- LeetCode 2610. 转换二维数组
迪小莫学AI
每日算法leetcode算法数据结构
LeetCode2610.转换二维数组题目描述给定一个整数数组nums,请你创建一个满足以下条件的二维数组:二维数组应该只包含数组nums中的元素。二维数组中的每一行都包含不同的整数。二维数组的行数应尽可能少。返回结果数组。如果存在多种答案,则返回其中任何一种。注意:二维数组的每一行上可以存在不同数量的元素。示例示例1:输入:nums=[1,3,4,1,2,3,1]输出:[[1,3,4,2],[1
- 算法-动态规划-最大子数组和
程序员南飞
算法动态规划leetcodejava开发语言数据结构职场和发展
力扣题目:53.最大子数组和53.描述:给你一个整数数组nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。示例1:输入:nums=[-2,1,-3,4,-1,2,1,-5,4]输出:6解释:连续子数组 [4,-1,2,1]的和最大,为 6。示例2:输入:nums=[1]输出:1示例3:输入:nums=[5,4,-1,7,8]输出:2
- 算法-合并区间
程序员南飞
算法数据结构职场和发展java动态规划
力扣题目:56.合并区间-力扣(LeetCode)题目描述:以数组intervals表示若干个区间的集合,其中单个区间为intervals[i]=[starti,endi]。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。示例1:输入:intervals=[[1,3],[2,6],[8,10],[15,18]]输出:[[1,6],[8,10],[15,18]]
- 算法通关----除自己自身以外数组乘积
fang4084
算法通关算法
题目来源:leetcode--238题目内容:给你一个整数数组nums,返回数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积。题目数据保证数组nums之中任意元素的全部前缀元素和后缀的乘积都在32位整数范围内。请不要使用除法,且在O(n)时间复杂度内完成此题。示例1:输入:nums=[1,2,3,4]输出:[24,12,8,6]示例2:输入:nums=[-
- python-leetcode-除自身以外数组的乘积
Joyner2018
pythonleetcode算法职场和发展
238.除自身以外数组的乘积-力扣(LeetCode)classSolution:defproductExceptSelf(self,nums:List[int])->List[int]:n=len(nums)#初始化结果数组answer=[1]*n#计算前缀乘积prefix=1foriinrange(n):answer[i]=prefixprefix*=nums[i]#计算后缀乘积,同时更新结果
- 力扣刷题笔记_动态规划爬楼梯问题
yma16
csp算法题目学习
题目描述假设你正在爬楼梯。需要n阶你才能到达楼顶。每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定n是一个正整数。示例一输入:2输出:2解释:有两种方法可以爬到楼顶。方法一:1阶+1阶方法二:2阶示例二输入:3输出:3解释:有三种方法可以爬到楼顶。方法一:1阶+1阶+1阶方法二:1阶+2阶方法三:2阶+1阶动态规划它的最优解可以从其子问题的最优解来有效地构建。第i阶可以由以
- LeetCode第92题_反转链表II
@蓝莓果粒茶
算法leetcode链表算法c++数据结构python后端
LeetCode第92题:反转链表II题目描述给你单链表的头指针head和两个整数left和right,其中left1->2->3->4->5|prev|curr找到left前一个节点prev(即节点1):dummy->1->2->3->4->5||prevcurr第一次头插:将节点3插入到prev之后:dummy->1->3->2->4->5||prevcurr第二次头插:将节点4插入到prev
- Java开发中,spring mvc 的线程怎么调用?
小麦麦子
springmvc
今天逛知乎,看到最近很多人都在问spring mvc 的线程http://www.maiziedu.com/course/java/ 的启动问题,觉得挺有意思的,那哥们儿问的也听仔细,下面的回答也很详尽,分享出来,希望遇对遇到类似问题的Java开发程序猿有所帮助。
问题:
在用spring mvc架构的网站上,设一线程在虚拟机启动时运行,线程里有一全局
- maven依赖范围
bitcarter
maven
1.test 测试的时候才会依赖,编译和打包不依赖,如junit不被打包
2.compile 只有编译和打包时才会依赖
3.provided 编译和测试的时候依赖,打包不依赖,如:tomcat的一些公用jar包
4.runtime 运行时依赖,编译不依赖
5.默认compile
依赖范围compile是支持传递的,test不支持传递
1.传递的意思是项目A,引用
- Jaxb org.xml.sax.saxparseexception : premature end of file
darrenzhu
xmlprematureJAXB
如果在使用JAXB把xml文件unmarshal成vo(XSD自动生成的vo)时碰到如下错误:
org.xml.sax.saxparseexception : premature end of file
很有可能时你直接读取文件为inputstream,然后将inputstream作为构建unmarshal需要的source参数。InputSource inputSource = new In
- CSS Specificity
周凡杨
html权重Specificitycss
有时候对于页面元素设置了样式,可为什么页面的显示没有匹配上呢? because specificity
CSS 的选择符是有权重的,当不同的选择符的样式设置有冲突时,浏览器会采用权重高的选择符设置的样式。
规则:
HTML标签的权重是1
Class 的权重是10
Id 的权重是100
- java与servlet
g21121
servlet
servlet 搞java web开发的人一定不会陌生,而且大家还会时常用到它。
下面是java官方网站上对servlet的介绍: java官网对于servlet的解释 写道
Java Servlet Technology Overview Servlets are the Java platform technology of choice for extending and enha
- eclipse中安装maven插件
510888780
eclipsemaven
1.首先去官网下载 Maven:
http://www.apache.org/dyn/closer.cgi/maven/binaries/apache-maven-3.2.3-bin.tar.gz
下载完成之后将其解压,
我将解压后的文件夹:apache-maven-3.2.3,
并将它放在 D:\tools目录下,
即 maven 最终的路径是:D:\tools\apache-mave
- jpa@OneToOne关联关系
布衣凌宇
jpa
Nruser里的pruserid关联到Pruser的主键id,实现对一个表的增删改,另一个表的数据随之增删改。
Nruser实体类
//*****************************************************************
@Entity
@Table(name="nruser")
@DynamicInsert @Dynam
- 我的spring学习笔记11-Spring中关于声明式事务的配置
aijuans
spring事务配置
这两天学到事务管理这一块,结合到之前的terasoluna框架,觉得书本上讲的还是简单阿。我就把我从书本上学到的再结合实际的项目以及网上看到的一些内容,对声明式事务管理做个整理吧。我看得Spring in Action第二版中只提到了用TransactionProxyFactoryBean和<tx:advice/>,定义注释驱动这三种,我承认后两种的内容很好,很强大。但是实际的项目当中
- java 动态代理简单实现
antlove
javahandlerproxydynamicservice
dynamicproxy.service.HelloService
package dynamicproxy.service;
public interface HelloService {
public void sayHello();
}
dynamicproxy.service.impl.HelloServiceImpl
package dynamicp
- JDBC连接数据库
百合不是茶
JDBC编程JAVA操作oracle数据库
如果我们要想连接oracle公司的数据库,就要首先下载oralce公司的驱动程序,将这个驱动程序的jar包导入到我们工程中;
JDBC链接数据库的代码和固定写法;
1,加载oracle数据库的驱动;
&nb
- 单例模式中的多线程分析
bijian1013
javathread多线程java多线程
谈到单例模式,我们立马会想到饿汉式和懒汉式加载,所谓饿汉式就是在创建类时就创建好了实例,懒汉式在获取实例时才去创建实例,即延迟加载。
饿汉式:
package com.bijian.study;
public class Singleton {
private Singleton() {
}
// 注意这是private 只供内部调用
private static
- javascript读取和修改原型特别需要注意原型的读写不具有对等性
bijian1013
JavaScriptprototype
对于从原型对象继承而来的成员,其读和写具有内在的不对等性。比如有一个对象A,假设它的原型对象是B,B的原型对象是null。如果我们需要读取A对象的name属性值,那么JS会优先在A中查找,如果找到了name属性那么就返回;如果A中没有name属性,那么就到原型B中查找name,如果找到了就返回;如果原型B中也没有
- 【持久化框架MyBatis3六】MyBatis3集成第三方DataSource
bit1129
dataSource
MyBatis内置了数据源的支持,如:
<environments default="development">
<environment id="development">
<transactionManager type="JDBC" />
<data
- 我程序中用到的urldecode和base64decode,MD5
bitcarter
cMD5base64decodeurldecode
这里是base64decode和urldecode,Md5在附件中。因为我是在后台所以需要解码:
string Base64Decode(const char* Data,int DataByte,int& OutByte)
{
//解码表
const char DecodeTable[] =
{
0, 0, 0, 0, 0, 0
- 腾讯资深运维专家周小军:QQ与微信架构的惊天秘密
ronin47
社交领域一直是互联网创业的大热门,从PC到移动端,从OICQ、MSN到QQ。到了移动互联网时代,社交领域应用开始彻底爆发,直奔黄金期。腾讯在过去几年里,社交平台更是火到爆,QQ和微信坐拥几亿的粉丝,QQ空间和朋友圈各种刷屏,写心得,晒照片,秀视频,那么谁来为企鹅保驾护航呢?支撑QQ和微信海量数据背后的架构又有哪些惊天内幕呢?本期大讲堂的内容来自今年2月份ChinaUnix对腾讯社交网络运营服务中心
- java-69-旋转数组的最小元素。把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个排好序的数组的一个旋转,输出旋转数组的最小元素
bylijinnan
java
public class MinOfShiftedArray {
/**
* Q69 旋转数组的最小元素
* 把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个排好序的数组的一个旋转,输出旋转数组的最小元素。
* 例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
*/
publ
- 看博客,应该是有方向的
Cb123456
反省看博客
看博客,应该是有方向的:
我现在就复习以前的,在补补以前不会的,现在还不会的,同时完善完善项目,也看看别人的博客.
我刚突然想到的:
1.应该看计算机组成原理,数据结构,一些算法,还有关于android,java的。
2.对于我,也快大四了,看一些职业规划的,以及一些学习的经验,看看别人的工作总结的.
为什么要写
- [开源与商业]做开源项目的人生活上一定要朴素,尽量减少对官方和商业体系的依赖
comsci
开源项目
为什么这样说呢? 因为科学和技术的发展有时候需要一个平缓和长期的积累过程,但是行政和商业体系本身充满各种不稳定性和不确定性,如果你希望长期从事某个科研项目,但是却又必须依赖于某种行政和商业体系,那其中的过程必定充满各种风险。。。
所以,为避免这种不确定性风险,我
- 一个 sql优化 ([精华] 一个查询优化的分析调整全过程!很值得一看 )
cwqcwqmax9
sql
见 http://www.itpub.net/forum.php?mod=viewthread&tid=239011
Web翻页优化实例
提交时间: 2004-6-18 15:37:49 回复 发消息
环境:
Linux ve
- Hibernat and Ibatis
dashuaifu
Hibernateibatis
Hibernate VS iBATIS 简介 Hibernate 是当前最流行的O/R mapping框架,当前版本是3.05。它出身于sf.net,现在已经成为Jboss的一部分了 iBATIS 是另外一种优秀的O/R mapping框架,当前版本是2.0。目前属于apache的一个子项目了。 相对Hibernate“O/R”而言,iBATIS 是一种“Sql Mappi
- 备份MYSQL脚本
dcj3sjt126com
mysql
#!/bin/sh
# this shell to backup mysql
#
[email protected] (QQ:1413161683 DuChengJiu)
_dbDir=/var/lib/mysql/
_today=`date +%w`
_bakDir=/usr/backup/$_today
[ ! -d $_bakDir ] && mkdir -p
- iOS第三方开源库的吐槽和备忘
dcj3sjt126com
ios
转自
ibireme的博客 做iOS开发总会接触到一些第三方库,这里整理一下,做一些吐槽。 目前比较活跃的社区仍旧是Github,除此以外也有一些不错的库散落在Google Code、SourceForge等地方。由于Github社区太过主流,这里主要介绍一下Github里面流行的iOS库。 首先整理了一份
Github上排名靠
- html wlwmanifest.xml
eoems
htmlxml
所谓优化wp_head()就是把从wp_head中移除不需要元素,同时也可以加快速度。
步骤:
加入到function.php
remove_action('wp_head', 'wp_generator');
//wp-generator移除wordpress的版本号,本身blog的版本号没什么意义,但是如果让恶意玩家看到,可能会用官网公布的漏洞攻击blog
remov
- 浅谈Java定时器发展
hacksin
java并发timer定时器
java在jdk1.3中推出了定时器类Timer,而后在jdk1.5后由Dou Lea从新开发出了支持多线程的ScheduleThreadPoolExecutor,从后者的表现来看,可以考虑完全替代Timer了。
Timer与ScheduleThreadPoolExecutor对比:
1.
Timer始于jdk1.3,其原理是利用一个TimerTask数组当作队列
- 移动端页面侧边导航滑入效果
ini
jqueryWebhtml5cssjavascirpt
效果体验:http://hovertree.com/texiao/mobile/2.htm可以使用移动设备浏览器查看效果。效果使用到jquery-2.1.4.min.js,该版本的jQuery库是用于支持HTML5的浏览器上,不再兼容IE8以前的浏览器,现在移动端浏览器一般都支持HTML5,所以使用该jQuery没问题。HTML文件代码:
<!DOCTYPE html>
<h
- AspectJ+Javasist记录日志
kane_xie
aspectjjavasist
在项目中碰到这样一个需求,对一个服务类的每一个方法,在方法开始和结束的时候分别记录一条日志,内容包括方法名,参数名+参数值以及方法执行的时间。
@Override
public String get(String key) {
// long start = System.currentTimeMillis();
// System.out.println("Be
- redis学习笔记
MJC410621
redisNoSQL
1)nosql数据库主要由以下特点:非关系型的、分布式的、开源的、水平可扩展的。
1,处理超大量的数据
2,运行在便宜的PC服务器集群上,
3,击碎了性能瓶颈。
1)对数据高并发读写。
2)对海量数据的高效率存储和访问。
3)对数据的高扩展性和高可用性。
redis支持的类型:
Sring 类型
set name lijie
get name lijie
set na
- 使用redis实现分布式锁
qifeifei
在多节点的系统中,如何实现分布式锁机制,其中用redis来实现是很好的方法之一,我们先来看一下jedis包中,有个类名BinaryJedis,它有个方法如下:
public Long setnx(final byte[] key, final byte[] value) {
checkIsInMulti();
client.setnx(key, value);
ret
- BI并非万能,中层业务管理报表要另辟蹊径
张老师的菜
大数据BI商业智能信息化
BI是商业智能的缩写,是可以帮助企业做出明智的业务经营决策的工具,其数据来源于各个业务系统,如ERP、CRM、SCM、进销存、HER、OA等。
BI系统不同于传统的管理信息系统,他号称是一个整体应用的解决方案,是融入管理思想的强大系统:有着系统整体的设计思想,支持对所有
- 安装rvm后出现rvm not a function 或者ruby -v后提示没安装ruby的问题
wudixiaotie
function
1.在~/.bashrc最后加入
[[ -s "$HOME/.rvm/scripts/rvm" ]] && source "$HOME/.rvm/scripts/rvm"
2.重新启动terminal输入:
rvm use ruby-2.2.1 --default
把当前安装的ruby版本设为默
![]() (根号下n需要向下取整)。那么对于在这个区间内的数 m,必然满足
(根号下n需要向下取整)。那么对于在这个区间内的数 m,必然满足![]() 表示正整数n的最少数量的完全平方和。则
表示正整数n的最少数量的完全平方和。则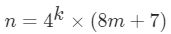 是否成立。
是否成立。