【计算机图形学】实验一 直线生成算法实现（实验报告分析+截图+源码）

可以先看一下这篇呀~【计算机图形学】专栏前言-CSDN博客https://blog.csdn.net/m0_55931547/article/details/135863062

一、实验目的

        理解基本图形元素光栅化的基本原理，掌握基本图形元素光栅化算法，利用OpenGL实现直线和圆光栅化。

二、实验内容

        (1) 根据所给的直线光栅化的示范源程序，在计算机上编译运行，输出正确结果，写入实验报告；

        (2) 指出示范程序采用的算法，以此为基础将其改造为中点线算法或Bresenham算法，写入实验报告；

        (3) 根据示范代码，将其改造为圆的光栅化算法，写入实验报告；

        (4) 了解和使用OpenGL的生成直线的命令，来验证程序运行结果。

三、实验原理

        示范代码参见教材直线光栅化一节中的DDA算法。下面介绍下OpenGL画线的一些基础知识和glutReshapeFunc()函数。

        （1）数学上的直线没有宽度，但OpenGL的直线则是有宽度的。同时，OpenGL的直线必须是有限长度，而不是像数学概念那样是无限的。可以认为，OpenGL的“直线”概念与数学上的“线段”接近，它可以由两个端点来确定。这里的线由一系列顶点顺次连结而成，有闭合和不闭合两种。

        前面的实验已经知道如何绘“点”，那么OpenGL是如何知道拿这些顶点来做什么呢？是一个一个的画出来，还是连成线？或者构成一个多边形？或是做其它事情呢？为了解决这一问题，OpenGL要求：指定顶点的命令必须包含在glBegin函数之后，glEnd函数之前（否则指定的顶点将被忽略），并由glBegin来指明如何使用这些点。

例如：

glBegin(GL_POINTS);

        glVertex2f(0.0f, 0.0f);

        glVertex2f(0.5f, 0.0f);

glEnd();

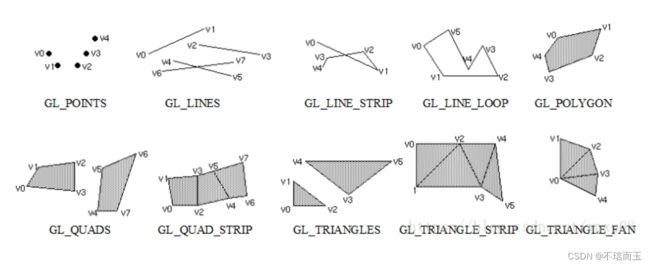
        则这两个点将分别被画出来。如果将GL_POINTS替换成GL_LINES，则两个点将被认为是直线的两个端点，OpenGL将会画出一条直线。还可以指定更多的顶点，然后画出更复杂的图形。另一方面，glBegin支持的方式除了GL_POINTS和GL_LINES，还有GL_LINE_STRIP，GL_LINE_LOOP，GL_TRIANGLES，GL_TRIANGLE_STRIP，GL_TRIANGLE_FAN等，每种方式的大致效果如图A.2所示：

图A.2 OpenGL几何图元类型

        （2）首次打开窗口、移动窗口和改变窗口大小时，窗口系统都将发送一个事件，以通知程序员。如果使用的是GLUT，通知将自动完成，并调用向glutReshapeFunc()注册的函数。该函数必须完成下列工作：

        ①重新建立用作新渲染画布的矩形区域；

        ②定义绘制物体时使用的坐标系。

如：

void Reshape(int w, int h)

{

glViewport(0, 0, (GLsizei) w, (GLsizei) h);

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);

}

        在GLUT内部，将给该函数传递两个参数：窗口被移动或修改大小后的宽度和高度，单位为像素。glViewport()调整像素矩形，用于绘制整个窗口。接下来三个函数调整绘图坐标系，使左下角位置为（0， 0），右上角为（w, h）。

四、参考实验步骤

        （1）修改DDA算法，使之适用于各种不同斜率。完成Bresenham画线法和中点线算法程序函数，替换原来的直线生成算法并将其修改成适用于Visual Studio 2010开发平台的语法格式。

         （2）然后用中点画圆法画出任意大小的圆，先设定一个点为当前点亮像素，根据判别式选择下一个在圆外或圆内的点作为下一个点亮像素，调用的点亮函数为Cirpot( )。

        （3）最后调用myDisplay( )函数将已赋值的直线、圆、矩形等图形显示到屏幕上。

五、实验过程

5.1 DDA

5.1.1 题目

        根据所给的直线光栅化的示范源程序，在计算机上编译运行，输出正确结果，写入实验报告。

5.1.2 详细分析

初始化：

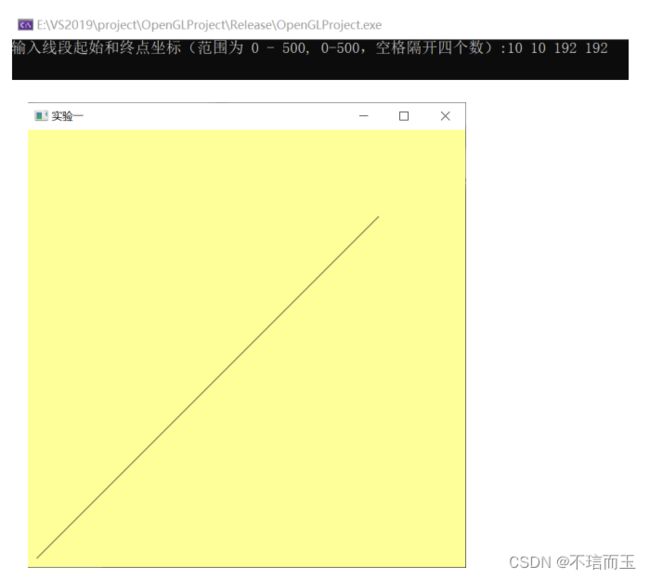
        首先由像素点的生成实验中可知，需要使用glutInit对GLUT进行初始化，这个函数必须在其它的GLUT使用之前调用一次；接着用glutInitDisplayMode设置显示方式，其中GLUT_RGB表示使用RGB颜色，GLUT_SINGLE表示使用单缓冲；接着用glutInitWindowPosition设置窗口在屏幕中的位置，glutInitWindowSize设置窗口的大小， glutCreateWindow根据前述设置的信息创建窗口，其中参数“实验一”作为窗口的标题；接着使用glClearColor将清空颜色设为黄色，用glClear(GL_COLOR_BUFFER_BIT)将窗口的背景设置为当前清空颜色，也可以理解为设置背景颜色；接着使用gluOrtho2D将窗口的左下角设为（0，0），最后在调用glutDisplayFunc进行画图之前，先通过键盘输入需要绘制的直线的端点，存放在全局变量xs， ys， xe ， ye中。（glutMainLoop进行一个消息循环，现在只需知道这个函数可以显示窗口，并且等待窗口关闭后才会返回）

画直线：

        设置一个lineSegment专门用不同的方法画直线，现在里面只有一个DDA方法，DDA的算法流程如下：

        1）已知直线的两端点坐标：(x1，y1)，(x2，y2)

        2）计算两个方向的变化量：dx=x2－x1， dy=y2－y1

        3）求出两个方向最大变化量的绝对值：

                        steps=max(|dx|，|dy|)

        4）计算两个方向的增量(考虑了生成方向)：

                        xin=dx/steps

                        yin=dy/steps

        5）设置初始象素坐标：x=x1,y=y1

        6）用循环实现直线的绘制：

for(i=1；i<=steps；i++)

{ SetPixel(HDC，x，y，color)；/*在(x，y)处，以color色画点*/

x=x+xin；

y=y+yin；

}

 5.1.3 实验截图

 5.1.4 核心代码

void LineDDA(int x0, int y0, int x1, int y1) {
	int dx, dy, epsl, k;
	float x, y, xIncre, yIncre;
	dx = x1 - x0;
	dy = y1 - y0;
	x = x0;
	y = y0;
	if (abs(dx) > abs(dy))  epsl = abs(dx);
	else epsl = abs(dy);
	xIncre = (float)dx / (float)epsl;
	yIncre = (float)dy / (float)epsl;

	for (k = 0; k <= epsl; k++) {
		glVertex2i(int(x + 0.5), int(y + 0.5));
		x += xIncre;
		y += yIncre;
	}
}

5.2 中点Bresenham

5.2.1 题目

        指出示范程序采用的算法，以此为基础将其改造为中点线算法或Bresenham算法，写入实验报告；

5.2.2 详细分析

        示范程序所采用的算法是DDA算法。这里选择的是中点Bresenham算法，该算法流程如下：

（0<=k<=1）

1. 已知直线的两端点坐标：(x0，y0)，(x1，y1)
2. 计算初始值dx和dy，d=dx-2dy，x=x0，y=y0
3. 绘制点（x，y）。判断d的符号，若d<0，则（x，y）更新为（x+1，y+1），d更新为d+2dx-2dy；否则（x，y）更新为（x+1，y），d更新为d-2dy。
4. 当直线没有画完时重复步骤3），否则结束

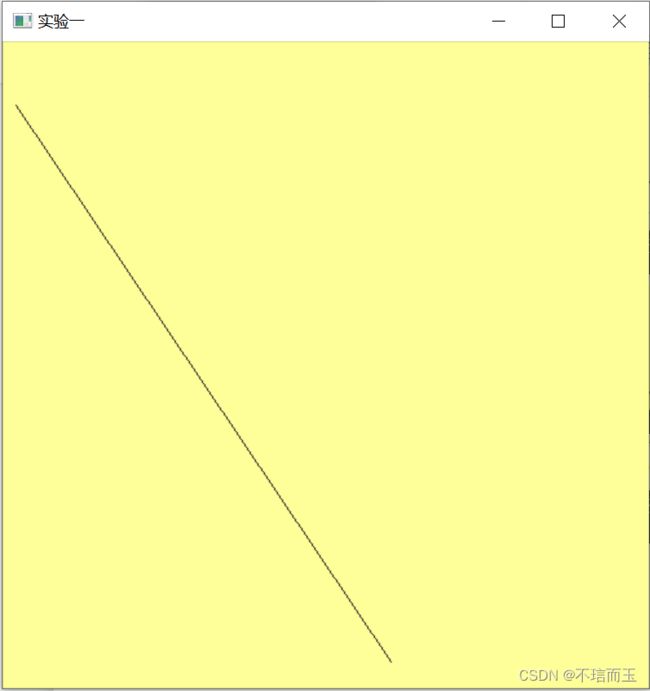
        Bresenham算法对任意斜率的直线段具有通用性，对于斜率为整且大于1的直线段，只需要交换x和y之间的规则。对于负斜率，除了一个坐标递减而另一个坐标递增外，其余程序是类似的，也即初始条件以及增量不同：        

 5.2.3 结果截图

 5.2.4 核心代码

void MidpointBresenham(int x0, int y0, int x1, int y1)    //中点Bresenham算法画线
{
    int dx, dy, d, UpIncre, DownIncre, x, y;
    //使dx总为正，方便分情况讨论
    if (x0 > x1) {
        x = x1; x1 = x0; x0 = x;
        y = y1; y1 = y0; y0 = y;
    }
    x = x0, y = y0;
    dx = x1 - x0;
    dy = y1 - y0;
    if (dy > 0 && dy <= dx) {    //0= (-dx)) && dy <= 0) //-1<=k<=0
    {
        d = dx - 2 * dy;
        UpIncre = -2 * dy;
        DownIncre = -2 * dx - 2 * dy;
        while (x <= x1)
        {
            glVertex2i(x, y);
            x++;
            if (d > 0)
            {
                y--;
                d += DownIncre;
            }
            else d += UpIncre;
        }
    }
    else if (dy < (-dx)) //k<-1
    {
        d = -dy - 2 * dx;
        UpIncre = 2 * dx + 2 * dy;
        DownIncre = 2 * dx;
        while (y >= y1)
        {
            glVertex2i(x, y);
            y--;
            if (d < 0)
            {
                x++;
                d -= UpIncre;
            }
            else d -= DownIncre;
        }
    }

    else //k>1和k不存在
    {
        d = dy - 2 * dx;
        UpIncre = 2 * dy - 2 * dx;
        DownIncre = -2 * dx;
        while (y <= y1)
        {
            glVertex2i(x, y);
            y++;
            if (d < 0)
            {
                x++;
                d += UpIncre;
            }
            else d += DownIncre;
        }
    }
}

 5.3 中点Bresenham画圆

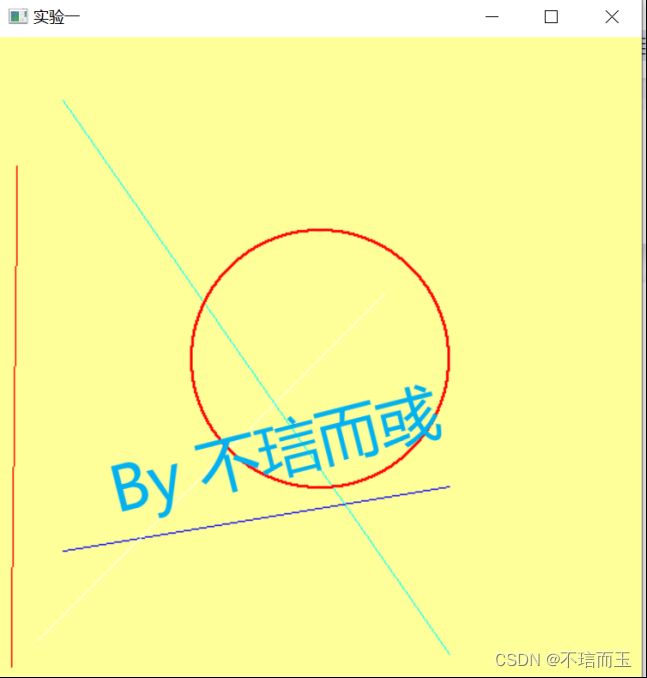
5.4 OpenGL的生成直线的命令

5.5 调用myDisplay( )函数显示

贴麻了，基本上画直线的两个重点算法都在这里了，如果还需要其他的大家自己下载资源看吧✧(≖ ◡ ≖✿)

下面这个资源仅是实验一的源码和实验报告： 

【计算机图形学】直线生成算法实现-其他文档类资源-CSDN文库https://download.csdn.net/download/m0_55931547/85811017

如果是开了专栏的朋友，实验一的和实验二的资源放到一起了哟，请移步【计算机图形学】实验二 几何变换（实验报告分析+截图+源码）_1. 本关任务 (1) 理解几何变换基本原理, 掌握平移、旋转、缩放变换的方法; (2) 根-CSDN博客https://blog.csdn.net/m0_55931547/article/details/131078982