【leetcode】55-跳跃游戏【C/C++】

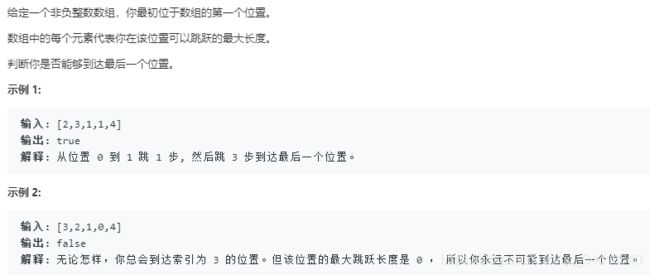
题目如下：

解题思路：

方法一：

首先想到的是从前向后遍历数组，根据当前元素的大小逐一选择跳跃位置，深度搜索+回溯。但是该方法对于大规模数组时间复杂度过高，因为其不存在剪枝的过程，会遍历整个数组的每一种可能。

代码如下：

class Solution {
public:
    bool canJump(vector& nums) {
        int l = nums.size();
        return bfs_canJump(l, 0, nums);
    }
    
    //k是跳跃数组时的当前下标
    bool bfs_canJump(int l, int k, vector& nums){
        if(nums[k] == 0 && k < l-1) //遇到为0的非末尾元素，不可能跳到最后
            return false;
        else if(k + nums[k] >= l-1)
            return true;
        for(int i = 1; i <= nums[k] && k + i <= l-1; i++){
            if(bfs_canJump(l, k+i, nums))
                return true;
        }
        return false;
    }
};

 方法二：

从后向前遍历数组，采用贪心算法的思路。

• 即从最后一位（当前位）向前寻找，每当 当前最后一位 可由 前一位 可以到达时，那么 当前最后一位 及其后面就不用再考虑，因为任何走法一定可以从 前一位 走到 当前最后一位（当前最后一位）。
• 若 当前最后一位 不可由 前一位 到达，继续向前寻找，若直到找到第一位仍未找到则结束，返回失败；否则返回成功。

代码如下：

class Solution {
public:
    bool canJump(vector& nums) {
        int lastposition = nums.size() - 1;
        for(int i = nums.size() - 2; i >= 0; i--){
            if(nums[i] + i >= lastposition) //当前lastposition的之前位可达当前lastposition
                lastposition  = i; //则更新lastposition
        }
        if(lastposition == 0)
            return true;
        return false;
    }
};