算法基础课04:离散化与区间合并
1.离散化
1.1基本含义
离散化的基本含义:把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。通俗的说,离散化是在不改变数据相对大小的条件下,对数据进行相应的缩小。
注意: 本篇所讲离散化,特指对一个保序的整数序列进行离散化。
1.2使用背景
一般而言,需要在这样的情况下使用离散化:有一些数字,它们的值域范围很大,但这些数字在值域中分布很稀疏(比如值域为【0,10^9】,但相对地数字个数很少,只有10^5个左右)。而在某些题目中,你需要以这些数字为下标开数组,但实际上你无法开一个很大的数组(无法开一个长度为10^9的数组......)。因此,需要把这些数字序列映射到从0开始的连续的自然数中,这样数组长度等于数字的个数(一个不大的数)。这一过程称为离散化。
举一个例子:
假设有数字:1 ,3,100,2000,500000。那么,这些数字的值域为【1,500000】,而实际上这些数字只有5个。若要以这些数字为下标创建一个数组,不管能不能开那么大的数组,都会造成极大的空间浪费。如果我们把这五个数字根据大小依次映射为0,1,2,3,4这五个数,只需要开一个很小的数组即可。
要使用离散化主要就是解决两个关键问题:
①数组 a[ ] 中可能有重复元素,如何去重;
②给出一个下标 x ,如何算出 x 离散化后的值。由于我们要求数字序列是有序的,因此我们可以采用二分的方法来计算 x 离散化后的值。
1.3离散化模板
其基本步骤可以概况如下:
①用一个辅助数组存储要离散的所有坐标 x;
②将这些坐标排序;
③去重,保证相同的元素离散化后数字相同;
④二分法得到坐标 x 离散化后的值,这个值就是原数组下标。
C++代码模板
vector alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
} 1.4例题:AcWing 802. 区间和
假定有一个无限长的数轴,数轴上每个坐标上的数都是 0。
现在,我们首先进行 n 次操作,每次操作将某一位置 x 上的数加 c。
接下来,进行 m 次询问,每个询问包含两个整数 l 和 r,你需要求出在区间 [l,r] 之间的所有数的和。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含两个整数 x 和 c。
再接下来 m 行,每行包含两个整数 l 和 r。
输出格式
共 m 行,每行输出一个询问中所求的区间内数字和。
数据范围
![]()
![]()
![]()
![]()
输入样例
3 3
1 2
3 6
7 5
1 3
4 6
7 8输出样例
8
0
5C++代码实现如下
#include
#include
#include
using namespace std;
const int N = 300010; //n次插入和m次查询相关数据量的上界
typedef pair PII; //所有操作都要读入两个数,用pair来存
int a[N] , s[N]; //a[]用于存数,s[]是前缀和
vector alls; //待离散化的坐标
vector add , query; //add为插入操作,query为询问操作,其中第一个元素为下标,第二个元素为值
//二分求出x对应离散化后的值
int find(int x){ //找到第一个 >= x 的位置
int l = 0 , r = alls.size() - 1;
while(l < r){
int mid = l + r >> 1;
if(alls[mid] >= x)
r = mid;
else
l = mid + 1;
}
return r + 1; //映射到 1,2,...,n
}
int main(){
int n , m;
cin >> n >> m;
for(int i = 0; i < n; i ++){ //n次操作
int x , c;
cin >> x >> c;
add.push_back({x , c}); //在下标为 x 的位置加上 c
alls.push_back(x); //把下标 x 加到待离散化数组中
}
for(int i = 0; i < m; i ++){ //m次查询
int l , r;
cin >> l >> r; //区间端点坐标
query.push_back({l , r}); //把l、r加入到query
//所有区间左右端点加入到待离散化数组中,L、R下标可能没有对应元素,但查询时候会用到,所以也要离散化
alls.push_back(l);
alls.push_back(r);
}
//去重
sort(alls.begin() , alls.end());
alls.erase(unique(alls.begin() , alls.end()),alls.end());
//处理插入
for(auto item : add){
int x = find(item.first); //把插入add数组中的所有元素的下标映射
a[x] += item.second; //形成映射后新的 下标-值 关系
}
//预处理前缀和
for(int i = 1; i <= alls.size(); i ++)
s[i] = s[i - 1] + a[i];
//询问
for(auto item : query){
int l = find(item.first) , r = find(item.second); //要查询的l、r要做映射
cout << s[r] - s[l - 1] << endl; //部分前缀和公式
}
return 0;
} 对于本题离散化的解析有一篇非常赞的文章:AcWing 802. 画个图辅助理解~
2.区间合并
2.1基本含义
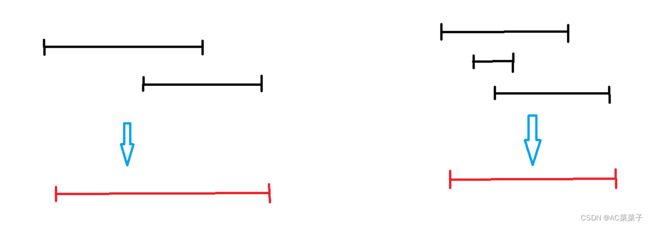
给出多个区间,若某些区间有交集则合并为一个区间。
2.2边界问题
两个区间若只有端点相交,则也算可以合并。
2.3基本思路
1.按区间左端点进行排序
2.扫描整个区间,把所有可能有交集的区间进行合并:
(1)每次维护一个当前区间,设当前维护区间左端点为 st,右端点为 ed;
(2)假设当前扫描到的区间为第 i 个,则当前扫描区间与当前维护区间有如下三种关系:
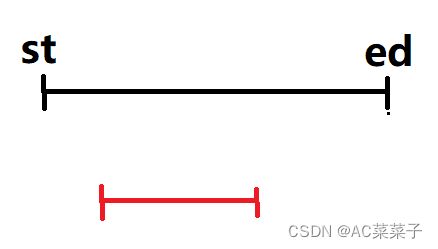
①当前扫描区间在当前维护区间内部:st 与 ed 不变,即当前维护区间不变;
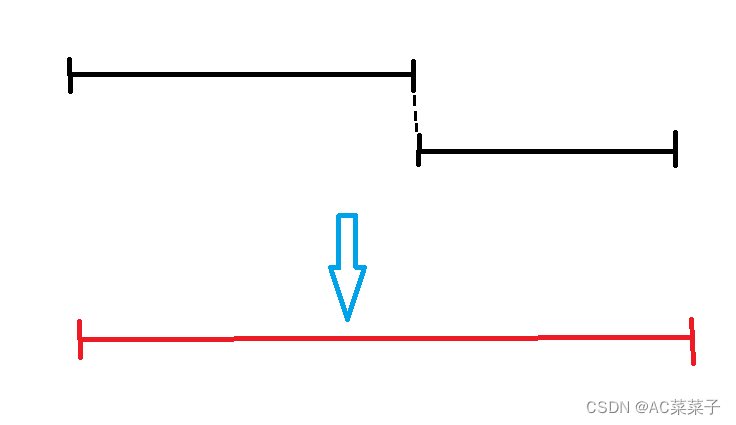
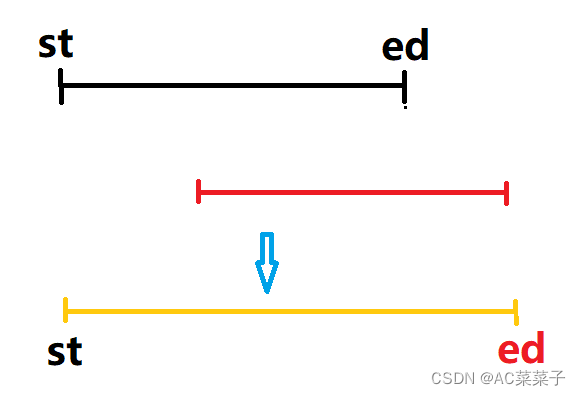
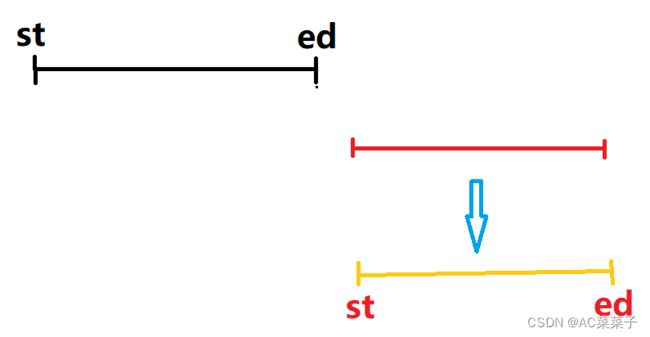
②当前扫描区间与当前维护区间有交集但不在其内部: st不变,ed变为当前扫描区间的右端点;
③当前扫描区间与当前维护区间无交集:由于各区间按左端点从小到大的顺序扫描,因此之后的所有区间的左端点一定是在当前扫描区间的左端点之后,与当前维护区间没有交集。因此当前维护区间已是一个完成合并的区间。此时当前扫描区间的左右端点变为新的 st 和 ed。
为什么不会出现当前扫描区间左端点在当前维护区间左端点的左边这种情况呢?还是因为各区间是按从小到大的顺序进行扫描的。
2.4样例模拟
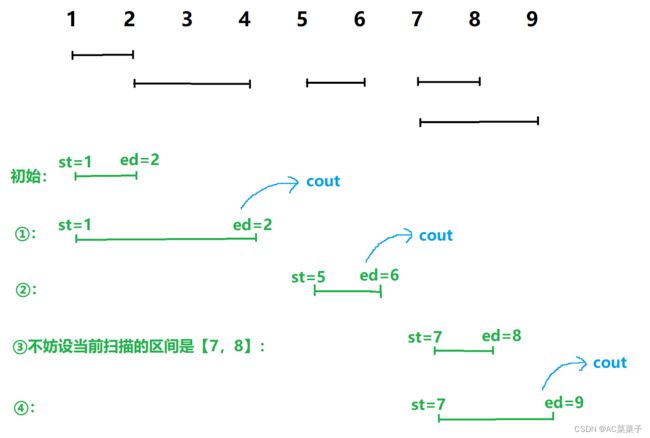
有如下区间:【1,2】、【2,4】、【5,6】、【7,8】、【7,9】,将各区间合并然后统计合并后的区间数量。
C++代码模板
typedef pair PII;
vector segs;
void merge(vector &segs){
vector res; //存放结果
sort(segs.begin() , segs.end()); //优先按第一个值排序
//从前往后扫描并维护一个当前区间
int st = -2e9 , ed = -2e9; //初始时没有维护任何区间,可设一个边界值,其实就是-∞
for(auto seg : segs){
//第三种情况:当前维护区间严格位于扫描的区间的左边,没有任何交集,说明找到一个新区间
if(ed < seg.first){
if(st != -2e9) res.push_back({st , ed}); //如果不是初始时的边界值,则把该区间加入答案中
st = seg.first , ed = seg.second; //扫描区间变成当前维护区间
}
//第一、二种情况:当前维护区间与扫描区间是有交集的,更新ed为当前维护区间右端点与扫描区间右端点中的最大值
else ed = max(ed , seg.second);
}
//把最后一个区间加入答案中。此时的st,ed变量不需要继续维护,只需要放进res数组即可
if(st != -2e9) res.push_back({st , ed}); //主要是防止输入为空的情况
segs = res; //res相当于segs合并后的结果,最后把segs更新为res
}