一文读懂JPEG算法！附C++代码实现JPEG算法，实现从BMP到JPEG转换！

获取更多内容，请关注微信公众号“电路板上的一抹微笑”

写在前面： 

        本学期，博主在上一门现代通信技术双语课程，期末有一个小组Topic“Data Compression”，我被分到去简单梳理下JPEG、MPEG1-音频和MPEG1-视频三种编码压缩技术。想起博客好久没更新了，遂顺便水一期。嘿嘿。因为是双语课程，所以博主是用英语写的，但不要担心，我在英语段落下面，进行了翻译，觉得对您有用的话，请帮作者点个赞支持一下。下面正式开始JPEG讲解：

一、What is JPEG：

        JPEG（Joint Photographic Experts Group） is a standard for continuous tone still image compression. The file suffix is.jpg or.jpeg, which is the most commonly used image file format. It mainly adopts the joint encoding method of predictive coding (DPCM), discrete cosine transform (DCT) and entropy coding to remove redundant image and color data. It is a lossy compression format, which can compress the image in a small storage space, and to a certain extent will cause damage to the image data. In particular, if the compression ratio is too high, the image quality will be reduced after the final decompression. If the pursuit of high-quality image, it is not appropriate to use too high compression ratio.

        翻译：JPEG是用于连续色调静态图像压缩的一种标准，文件后缀名为.jpg或.jpeg，是最常用的图像文件格式。其主要是采用预测编码（DPCM）、离散余弦变换（DCT）以及熵编码的联合编码方式，以去除冗余的图像和彩色数据，属于有损压缩格式，它能够将图像压缩在很小的储存空间，一定程度上会造成图像数据的损伤。尤其是使用过高的压缩比例，将使最终解压缩后恢复的图像质量降低，如果追求高品质图像，则不宜采用过高的压缩比例。 

        Lossy compression, which is to remove unimportant parts of the original data so that it can be stored in a smaller volume, such as the number 485194.200000000001, if we use 485194.2, is a "lossy" preservation method, Because the "0.000000000001" after the decimal point is not important, it can be ignored. JPEG's entire compression process basically follows this step:

        1. Divide data into "important parts" and "unimportant parts"

        2. Strain out the unimportant parts

        3. Save

        翻译：有损压缩，就是把原始数据中不重要的部分去掉，以便可以用更小的体积保存，比如485194.200000000001这个数，如果我们用485194.2来保存，就是一种“有损”的保存方法，因为小数点后面的那个“0.000000000001”属于不重要的部分，所以可以被忽略掉。JPEG整个压缩过程基本上也是遵循这个步骤：
        1. 把数据分为“重要部分”和“不重要部分”
        2. 滤掉不重要的部分
        3. 保存

二、Step of compression：

①Segmentation of image【图像分割】：Divide the image into 8 by 8 pixel chunks

        翻译：将图片分割成大小为8*8个像素的小块

        Q: What if the image can't be divided by an 8x8 matrix? For example 450x450 graph, jpg how to compress?

        A: General boundary extension, zero filling, periodic symmetry extension, etc.

        翻译：

        小问题：如果图像不能被8x8大小的矩阵分割怎么办?比如450x450的图，jpg如何压缩？

        答：一般边界拓展，补零，周期对称延拓等。【这里可以进行一个小的课堂互动】

figure 1 “Lenna”——The world's first JPG image

②RGB->YCbCr【颜色空间转换】

        "Color space" refers to the mathematical model that represents colors

        翻译：“颜色空间”，是指表达颜色的数学模型

figure 2 “RGB”Color space

        For example, the "RGB" model is to decompose the color into three components, red, green and blue, so that a picture can be decomposed into three grayscale images. Mathematically, every 8X8 pattern can be expressed into three 8X8 matrices, the range of which is generally between [0,255].

        In the JPEG compression algorithm, the pattern needs to be transformed into a YCbCr model, where Y represents Luminance, Cb and Cr represent the "chromatic aberration" of green and red respectively. The following is the mathematical relation between "RGB" and "YCbCr", and the coefficients are generally empirical values.

        翻译：

        例如“RGB”模型，就是把颜色分解成红绿蓝三种分量，这样一张图片就可以分解成三张灰度图，数学表达上，每一个8X8的图案，可以表达成三个8X8的矩阵，其中的数值的范围一般在[0,255]之间。

        在JPEG压缩算法中，需要把图案转换成为YCbCr模型，这里的Y表示亮度(Luminance)，Cb和Cr分别表示绿色和红色的“色差值”。以下是“RGB”转“YCbCr”的数学关系式，系数一般为经验值。

③DCT【离散余弦变换】

        According to the property of the discrete Fourier transform, the Fourier transform of the real even function only contains the real cosine term, so a kind of transform of the real number domain, the discrete cosine transform (DCT), is constructed.

        翻译：根据离散傅里叶变换的性质，实偶函数的傅里叶变换只含实的余弦项，因此构造了一种实数域的变换——离散余弦变换(DCT)。

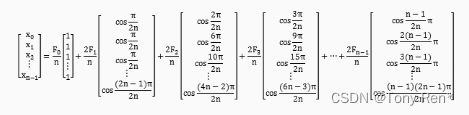
        The above equation is a DCT expression. As can be seen from the above equation, a group of one-dimensional data [x0,x1,x2...,xn-1] can be transformed into n transformation series Fi through DCT.

        翻译：上式为DCT表达式，从上式可知，一组一维数据[x0,x1,x2,…,xn-1],通过DCT变换后可以得到n个变换级数Fi。

        The above equation is IDCT transformation. After IDCT transformation, the original one-dimensional array can be decomposed into the sum of multiple arrays whose coefficients dB is the transformation series Fi, that is

        翻译：上式为IDCT变换，经过IDCT变换，就可以把原来的一个一维数组分解成系数分贝为变换级数Fi的多个数组的和来表示，即

Why do we use the DCT?

        DCT has a strong "energy concentration" characteristic: most natural signals (including sound and images) are concentrated in the low-frequency portion of the DCT, and when the signal has the statistical characteristics of Markov processes, The de-correlation of DCT is close to the performance of K-L transform (Karhunen-Loeve) transform - it has optimal de-correlation).

        翻译：离散余弦变换具有很强的"能量集中"特性:大多数的自然信号(包括声音和图像)的能量都集中在离散余弦变换后的低频部分，而且当信号具有接近马尔科夫过程(Markov processes)的统计特性时，离散余弦变换的去相关性接近于K-L变换(Karhunen-Loève）变换--它具有最优的去相关性)的性能。

        Let's take the y-component of the first image in the upper left corner of Lenna as an example, and the transformed matrix is

        翻译：我们以Lenna左上角第一块图像的Y分量为例，经过变换的矩阵为

figure3 The black block is the processing object

        It can be seen that after DCT conversion, the "energy" of the matrix is almost all concentrated on the DC component F(0,0) in the upper left corner, and the values in other positions are all very small. In other words, after DCT changes, the data is obviously divided into DC component and AC component, which has played a sufficient role in paving the way for further compression.

        翻译：可以看到，经过DCT转换，矩阵的“能量”几乎被全部集中在左上角上的直流分量F(0,0）上，其他位置的值都很小。也即数据经过DCT变化后，被明显分成了直流分量和交流分量两部分，为后面的进一步压缩起到了充分的铺垫作用。

        The purpose of DCT in the JPEG algorithm is twofold, the first is to make the coefficients as uncorrelated as possible, and the second is that the energy of the input signal should be included in the least number of coefficients as possible.

        翻译：在JPEG算法中进行DCT的目的有两个，第一是使系数尽可能不相关，第二是输入信号的能量应尽可能地包含到最少数目的系数中。

        Note that so far, the data is in a reversible state, i.e. no information is lost! Data quantization and Huffman coding are two processes that cause information loss!

        翻译：注意，到目前为止，数据都是可逆状态，即没有信息丢失！数据量化和霍夫曼编码这两个过程会引起信息丢失！

④Quantization of data【数据量化】

        JPEG provides the following quantization algorithm:

        翻译：JPEG提供的量子化算法如下：

        Where, G is the image matrix we need to process, and Q is called quantization coefficient matrix. The JPEG algorithm provides two standard quantization coefficient matrices for processing brightness data Y and chromatic aberration data Cr and Cb respectively.

        翻译：式中G是我们需要处理的图像矩阵，Q称作量化系数矩阵。JPEG算法提供了两种标准的量化系数矩阵，分别用于处理亮度数据Y和色差数据Cr以及Cb。

table 1 Standard luminance quantifier

table 2 Standard chromatic aberration quantization table

        The round function is an integer function

        翻译：round函数是取整函数

figure 4 Example of quantization process

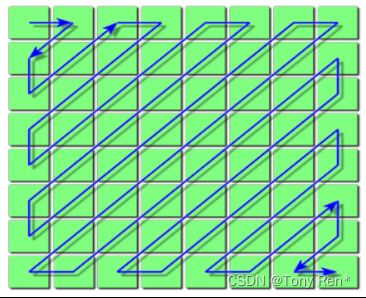
        After quantization, we need to transform the two-dimensional array obtained by quantization into a one-dimensional array for the convenience of subsequent Huffman coding. In the conversion, the order is as follows, since the zeros are mostly clustered in the bottom right corner, in this order you can put as many zeros together as possible.

        翻译：在量化后，我们需要把量化得到的二维数组转变为一维数组，以方便后续的霍夫曼编码。在转换时，顺序如下，因为0大部分集中在右下角，按此顺序可以尽可能地把0放在一起。

figure 5 Conversion sequence diagram

⑤Huffman coding【霍夫曼编码】

        The basic principle of JPEG coding is to adjust the encoding length of elements according to the frequency of use of elements in the data to get a higher compression ratio.

        翻译：霍夫曼编码的基本原理是根据数据中元素的使用频率，调整元素的编码长度，以得到更高的压缩比。

        In Huffman coding there are the following rules:

1. The non-zero data in the array and the number of zeros preceding the data are treated as a processing unit.
2. If the number of zeros in a cell exceeds 16, it is divided into groups of 16.
3. If the last cell is all zeros, it is represented by the special character "EOB". EOB means "the following data is all zeros".

        翻译：在JPEG编码中有如下规定： 将数组中非零的数据，以及数据前面0的个数作为一个处理单元。如果其中某个单元的0的个数超过16，则需要分成每16个一组，如果最后一个单元全都是0，则使用特殊字符“EOB”表示，EOB意思就是“后面的数据全都是0”。

        It can be found that the first two digits in the parentheses are between 0 and 15, so the two numbers can be combined into a byte. The high four digits are the number of the first 0, and the last four digits are the number of the following digits. According to this processing, the BIT encoding can be obtained

        翻译：可以发现，括号中前两个数字分都在0~15之间，所以这两个数可以合并成一个byte，高四位是前面0的个数，后四位是后面数字的位数，根据这一处理，可以得到BIT编码

        Note: The conversion from RLE encoding to BIT encoding is done according to the standard code table lookup provided by JPEG.

        翻译：注：从RLE编码转到BIT编码，是根据JPEG提供的标准码表查表完成。

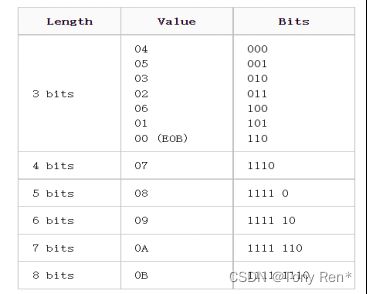
        For the encoding of the numbers before the parentheses, use the Huffman code. We complete this code according to the official Huffman code table.

        翻译：对于括号前面的数字的编码，就要使用霍弗曼编码。我们根据官方提供的霍弗曼编码表，完成这一编码。

table 3 DC Huffman code table

        According to table 3, we can know that the corresponding binary code of the DC part data 0x06 is "100".

        翻译：根据table 3,我们可以知道DC部分数据0x06，对应的二进制编码是“100”

        Finally, after Huffman encoding and serialization, the following table is obtained, where the serialized data is the data stored in jpeg.

        翻译：最终，经过霍夫曼编码和序列化后，可得到下表，其中序列化后的数据就是jpeg中存储的数据。

table 4 Huffman coding result

        On a computer, open any JPEG image in binary form and find the following contents:

        翻译：在电脑中，以二进制形式打开任意一张JPEG格式图片，发现其内容如下，

figure 6 JPEG's stored content

总结：

编码过程为

相应的解码过程（与编码过程类似，不再详述）为

三、Performance of JPEG：

        Its advantages are:

①It supports high compression rate, so the download speed of JPEG image is greatly accelerated;

② It can easily process 16.8M color, can reproduce the full color image;

③ In the process of image compression, the image format can be freely selected between the minimum file size (lowest image quality) and the maximum file size (highest image quality);

④The file size of this format is relatively small and the download speed is fast, which is conducive to the transmission in the case of the bandwidth is not "rich".

        Its disadvantages are:

① Not all browsers support the insertion of JPEG images into web pages;

② compression may cause loss of image quality, so it is not suitable to use this format to display high definition images.

        翻译：

        它的优点是：

        ①它支持极高的压缩率，因此JPEG图像的下载速度大大加快；

        ②它能够轻松地处理16.8M颜色，可以很好地再现全彩色的图像；

        ③在对图像的压缩处理过程中，该图像格式可以允许自由地在最小文件尺寸（最低图像质量）和最大文件尺寸（最高图像质量）之间选择；

        ④该格式的文件尺寸相对较小，下载速度快，有利于在带宽并不“富裕”的情况下传输。

        它的缺点是：

        ①并非所有的浏览器都支持将各种JPEG图像插入网页；

        ②压缩时，可能使图像的质量受到损失，因此不适宜用该格式来显示高清晰度的图像。

四、Implementation of JPEG：

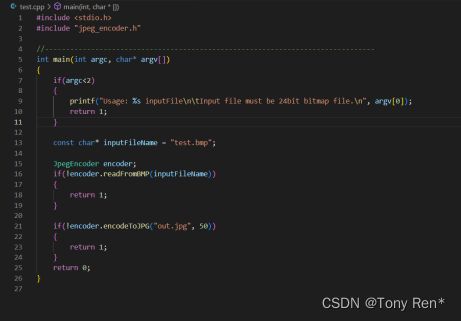
        ①主函数代码见下，输入为BMP格式图像，输出为JPEG格式图像，可以通过修改“encoderToJPG”函数中的参数，修改压缩比。

        ②通过g++编译生成a.exe文件，并输入参数“test.bmp”运行得到out.jpg

        ③查看压缩前后图片大小

figure 7 输入BMP图像大小

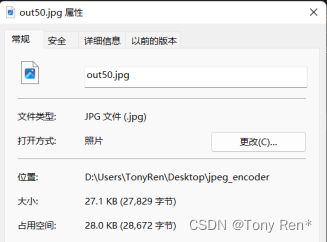
        当参数设定为50时，输出大小为

      figure 8 参数设为50时，输出图像的大小

        当参数设为100时，输出大小为

figure9 参数设为100时，输出图像的大小

figure 10 压缩前后图像对比

        由上图可知，通过JPEG算法，可以在保证一定图像质量的前提下，有效实现数据压缩。

代码连接：

 数据压缩JPEG算法的C++实现