数学建模 | 第一章 线性规划例题
第一章 线性规划例题篇
例1.1 某机床厂生产甲、乙两种机床,每台销售后的利润分别为 4000 元与 3000 元。生产甲机床需用A、B机器加工,加工时间分别为每台2小时和1小时;生产乙机床需用A、B、C三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
解:决策变量应设该厂生产x1台甲机床和x2台乙机床时总利润最大,则x1和x2应满足:
m a x max max z = 4 x 1 + 3 x 2 , z=4x_1+3x_2, z=4x1+3x2,
s . t . = { 2 x 1 + x 2 ≤ 10 , x 1 + x 2 ≤ 8 , x 2 ≤ 7 , x 1 , x 2 ≥ 0 。 s.t.=\begin{cases}2x_1+x_2\leq10,\\x_1+x_2\leq8,\\x_2\leq7,\\x_1,x_2\geq0。\end{cases} s.t.=⎩ ⎨ ⎧2x1+x2≤10,x1+x2≤8,x2≤7,x1,x2≥0。
化为Matlab标准型,即:
m i n min min w = − 4 x 1 − 3 x 2 , w=-4x_1-3x_2, w=−4x1−3x2,
s . t . = { [ 2 1 1 1 0 2 ] [ x 1 x 2 ] ≤ [ 10 8 7 ] , [ x 1 x 2 ] T ≥ [ 0 0 ] T 。 s.t.=\begin{cases}\left[\begin{matrix}2&1\\1&1\\0&2\end{matrix}\right]\left[\begin{matrix}x_1\\x_2\end{matrix}\right]\leq\left[\begin{matrix}10\\8\\7\end{matrix}\right],\\\left[\begin{matrix}x_1&x_2\end{matrix} \right]^T\geq\left[\begin{matrix}0&0\end{matrix}\right]^T。\end{cases} s.t.=⎩ ⎨ ⎧ 210112 [x1x2]≤ 1087 ,[x1x2]T≥[00]T。
答案:求得的最优解为x1=3.25,x2=3.5,对应的最优值z=23.5。
求解的Matlab程序为:
c = [-4,-3];
a = [2,1;1,1;0,2];
b = [10,8,7];
[x,y] = linprog(c,a,b,[],[],zeros(2,1))
x,y=-y
求解的Lingo程序为:
model:
sets:
col/1..2/:c,x;
row/1..3/:b;
lingks(row,col):a;
endsets
data:
c = 4 3;
a = 2 1 1 1 0 2;
b = 10 8 7;
enddata
max=@ sum(col:c*x);
@ for(row(i):@ sum(col(j):a(i,j)*x(j))<b(i));
end
例1.2 求解下列线性规划问题
m a x max max z = 2 x 1 + 3 x 2 − 5 x 3 , z=2x_1+3x_2−5x_3, z=2x1+3x2−5x3,
s . t . = { x 1 + x 2 + x 3 = 7 , 2 x 1 − 5 x 2 + x 3 ≥ 10 , x 1 + 3 x 2 + x 3 ≤ 12 , x 1 , x 2 , x 3 ≥ 0 。 s.t.=\begin{cases}x_1+x_2+x_3 = 7,\\2x_1-5x_2+x_3 \geq10,\\x_1+3x_2+x_3 \leq12,\\x_1, x_2 , x_3\geq0。\end{cases} s.t.=⎩ ⎨ ⎧x1+x2+x3=7,2x1−5x2+x3≥10,x1+3x2+x3≤12,x1,x2,x3≥0。
解:化为Matlab标准型,即:
m i n min min w = − 2 x 1 − 3 x 2 + 5 x 3 , w=-2x_1-3x_2+5x_3, w=−2x1−3x2+5x3,
s . t . = { [ − 2 5 − 1 1 3 1 ] [ x 1 x 2 x 3 ] ≤ [ − 10 12 ] , [ 1 1 1 ] ⋅ [ x 1 x 2 x 3 ] T = 7 , [ x 1 x 2 x 3 ] T ≥ [ 0 0 0 ] T 。 s.t.=\begin{cases}\left[\begin{matrix}-2&5&-1\\1&3&1\end{matrix}\right]\left[\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right]\leq\left[\begin{matrix}-10\\12\end{matrix}\right],\\\left[\begin{matrix}1&1&1\end{matrix} \right]·\left[\begin{matrix}x_1&x_2&x_3\end{matrix}\right]^T=7,\\\left[\begin{matrix}x_1&x_2&x_3\end{matrix} \right]^T\geq\left[\begin{matrix}0&0&0\end{matrix}\right]^T。\end{cases} s.t.=⎩ ⎨ ⎧[−2153−11] x1x2x3 ≤[−1012],[111]⋅[x1x2x3]T=7,[x1x2x3]T≥[000]T。
答案:求得的最优解为x1=6.4286,x2=0.5714,x3=0,对应的最优值z=14.5714
求解的Matlab程序为:
c=[-2;-3;5];
a=[-2,5,-1;1,3,1];
b=[-10;12];
aeq=[1,1,1];
beq=7;
[x,y]=linprog(c,a,b,aeq,beq,zeros(3,1))
x,y=-y % 最终解加负号,转换为最大值
求解的Lingo程序为:
model:
sets:
row/1..2/:b;
col/1..3/:c,x;
lingks(row,col):a;
endsets
data:
c = 2 3 -5;
a = -2 5 -1 1 3 1;
b = -10 12;
enddata
max=@ sum(col:c*x);
@ for(row(i):@ sum(col(j):a(i,j)*x(j))<b(i));
@ sum(col:x)=7;
end
例1.3 求解下列线性规划问题
m i n min min z = 2 x 1 + 3 x 2 + x 3 , z=2x_1+3x_2+x_3, z=2x1+3x2+x3,
s . t . = { x 1 + 4 x 2 + 2 x 3 ≥ 8 , 3 x 1 + 2 x 2 ≥ 6 , x 1 , x 2 , x 3 ≥ 0 。 s.t.=\begin{cases}x_1+4x_2+2x_3 \geq8,\\3x_1+2x_2 \geq6,\\x_1, x_2 , x_3\geq0。\end{cases} s.t.=⎩ ⎨ ⎧x1+4x2+2x3≥8,3x1+2x2≥6,x1,x2,x3≥0。
解:因为问题本身求解的是min值,所以无需再次化为Matlab标准型
答案:求得的最优解为x1=0.8066,x2=1.7900,x3=0.0166,对应的最优值z=7.0000
求解的Matlab程序为:
c=[2;3;1];
a=[1,4,2;3,2,0];
b=[8;6];
[x,y]=linprog(c,-a,-b,[],[],zeros(3,1)) %这里没有等式约束,所以为两个【】【】
求解的Lingo程序为:
model:
sets:
row/1..2/:b;
col/1..3/:c,x;
lingks(row,col):a;
endsets
data:
c = 2 3 1;
a = 1 4 2 3 2 0;
b = 8 6;
enddata
min=@ sum(col:c*x);
@ for(row(i):@sum(col(j):a(i,j)*x(j))>b(i));
end
例1.4 求解下列数学规划问题
m i n min min z = ∣ x 1 ∣ + 2 ∣ x 2 ∣ + 3 ∣ x 3 ∣ + 4 ∣ x 4 ∣ , z=|x_1|+2|x_2|+3|x_3|+4|x_4|, z=∣x1∣+2∣x2∣+3∣x3∣+4∣x4∣,
s . t . = { x 1 − x 2 + x 3 − x 4 ≤ − 2 , x 1 − x 2 + x 3 − 3 x 4 ≤ − 1 , x 1 − x 2 − 2 x 3 + 3 x 4 ≤ − 0.5 。 s.t.=\begin{cases}x_1-x_2+x_3-x_4 \leq-2,\\x_1-x_2+x_3-3x_4 \leq-1,\\x_1-x_2-2x_3+3x_4\leq-0.5。\end{cases} s.t.=⎩ ⎨ ⎧x1−x2+x3−x4≤−2,x1−x2+x3−3x4≤−1,x1−x2−2x3+3x4≤−0.5。
解:做变量变换 u i = x i + ∣ x i ∣ 2 u_i=\frac{x_i+|x_i|}{2} ui=2xi+∣xi∣和 v i = ∣ x i ∣ − x i 2 v_i=\frac{|x_i|-x_i}{2} vi=2∣xi∣−xi, i = 1 , 2 , 3 , 4 i=1,2,3,4 i=1,2,3,4,并把新变量重新排序成一维向量 y = [ u v ] = [ u 1 , … , u 4 , v 1 , … v 4 ] T y=\left[\begin{matrix}u\\v\end{matrix}\right]=\left[\begin{matrix}u_1,…,u_4,v_1,…v_4\end{matrix}\right]^T y=[uv]=[u1,…,u4,v1,…v4]T,则可把模型变换为线性规划模型:
m i n min min [ 1 , 2 , 3 , 4 , 1 , 2 , 3 , 4 ] T y \left[\begin{matrix}1,2,3,4,1,2,3,4\end{matrix}\right]^Ty [1,2,3,4,1,2,3,4]Ty
s . t . = { [ A − A ] [ u v ] ≤ [ − 2 − 1 − 0.5 ] T , y ≥ 0 。 s.t.=\begin{cases}\left[\begin{matrix}A&-A\end{matrix}\right]\left[\begin{matrix}u\\v\end{matrix}\right]\leq\left[\begin{matrix}-2&-1&-0.5\end{matrix}\right]^T,\\y\geq0。\end{cases} s.t.=⎩ ⎨ ⎧[A−A][uv]≤[−2−1−0.5]T,y≥0。
其中 A = [ 1 − 1 − 1 1 1 − 1 1 − 3 1 − 1 − 2 3 ] A=\left[\begin{matrix}1&-1&-1&1\\1&-1&1&-3\\1&-1&-2&3\end{matrix}\right] A= 111−1−1−1−11−21−33
答案:求得的最优解为x1=-2,x2=x3=x4=0,对应的最优值z=-2
求解的Matlab程序为:
clc,clear
c=1:4;c=[c,c]'; %构造价值列向量
a=[1 -1 -1 1;1 -1 1 -3;1 -1 -2 3];
a=[a,-a]; %构造变换后新的系数矩阵
b=[-2 -1 -1/2]';
[y,z]=linprog(c,a,b,[],[],zeros(8,1)) %这里没有等式约束,对应的矩阵为空矩阵
x=y(1:4)-y(5:end) %变换到原问题的解,x=u-v
求解的Lingo程序为:
model:
sets:
row/1..2/:b;
col/1..3/:c,x;
lingks(row,col):a;
endsets
data:
c = 2 3 1;
a = 1 4 2 3 2 0;
b = 8 6;
enddata
min=@ sum(col:c*x);
@ for(row(i):@sum(col(j):a(i,j)*x(j))>b(i));
end
例1.5 求解下列线性规划问题
m i n min min z = x 1 + x 2 , z=x_1+x_2, z=x1+x2,
s . t . = { 2 x 1 + 4 x 2 = 5 , x 1 ≥ 0 , x 2 ≥ 0 。 s.t.=\begin{cases}2x_1+4x_2=5,\\x_1\geq0,x_2\geq0。\end{cases} s.t.={2x1+4x2=5,x1≥0,x2≥0。
解:显然这是一个简单的二元一次方程联立求解,之所以此处有本例题,旨在说明该线性规划问题有最优实数解,但是对应的整数规划无可行解。
答案:求得的最优解为x1=0,x2=1.25,对应的最优值z=1.25
例1.6 求解下列线性规划问题
m i n min min z = x 1 + x 2 , z=x_1+x_2, z=x1+x2,
s . t . = { 2 x 1 + 4 x 2 = 6 , x 1 ≥ 0 , x 2 ≥ 0 。 s.t.=\begin{cases}2x_1+4x_2=6,\\x_1\geq0,x_2\geq0。\end{cases} s.t.={2x1+4x2=6,x1≥0,x2≥0。
解:同例1.5,本例题旨在说明该线性规划问题有最优实数解,若限制为整数,有可行解但最优解值变差。
答案:求得的最优解为x1=0,x2=1.5,对应的最优值z=1.5;若限制为整数,得x1=1,x2=1,对应的最优值z=2
例1.7 (随机取样法) y = x 2 y=x^2 y=x2、 y = 12 − x y=12-x y=12−x与 x x x轴在第一象限围成一个曲边三角形。设计一个随机实验,求该图形面积的近似值。
解:设计的随机试验的思想如下:在矩形区域 [ 0 , 12 ] × [ 0 , 9 ] [0,12]\times[0,9] [0,12]×[0,9]上产生服从均匀分布的107个随机点,统计随机点落在曲边三角形的频数,则曲边三角形的面积近似为上述矩阵的面积乘以频率。
答案:该图形面积的近似值在49.5附近,由于是随机模拟,每次的结果都是不一样的。
求解的Matlab程序为:
clc,clear
x=unifrnd(0,12,[1,10000000]);
y=unifrnd(0,9,[1,10000000]);
pinshu=sum(y<x.^2&x<=3)+sum(y<12-x&x>=3);
area_appr=12*9*pinshu/10^7
例1.8 (指派问题)求解下列指派问题,已知指派矩阵为
[ 3 8 2 10 3 8 7 2 9 7 6 4 2 7 5 8 4 2 3 5 9 10 6 9 10 ] \left[\begin{matrix}3&8&2&10&3\\8&7&2&9&7\\6&4&2&7&5\\8&4&2&3&5\\9&10&6&9&10\end{matrix}\right] 3868987441022226109739375510
解:这里需要把二维决策变量 x i j ( i , j = 1 , … 5 ) x_{ij}(i,j=1,…5) xij(i,j=1,…5)变成一维决策变量 y k ( k = 1 , … , 25 ) y_k(k=1,…,25) yk(k=1,…,25)。
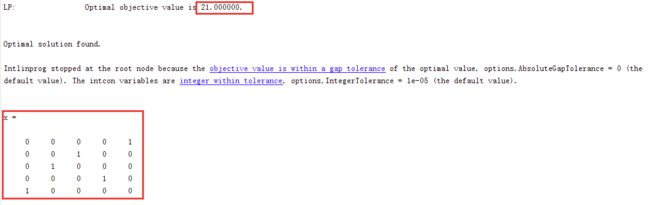
答案:求得的最优指派方案为 x 15 = x 23 = x 32 = x 44 = x 51 = 1 x_{15}=x_{23}=x_{32}=x_{44}=x_{51}=1 x15=x23=x32=x44=x51=1,最优值为21。
求解的Matlab程序为:
clc,clear
c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5;8 4 2 3 5;9 10 6 9 10];
c=c(:);a=zeros(10,25);intcon=1:25;
for i=1:5
a(i,(i-1)*5+1:5*i)=1;
a(5+i,i:5:25)=1;
end
b=ones(10,1);lb=zeros(25,1);ub=ones(25,1);
x=intlinprog(c,intcon,[],[],a,b,lb,ub);
x=reshape(x,[5,5])
model:
sets:
var/1..5/;
link(var,var):c,x;
endsets
data:
c=3 8 2 10 3
8 7 2 9 7
6 4 2 7 5
8 4 2 3 5
9 10 6 9 10;
enddata
min=@ sum(link:c*x);
@ for(var(i):@ sum(var(j):x(i,j))=1);
@ for(var(j):@ sum(var(i):x(i,j))=1);
@ for(link:@ bin(x));
end
例1.9 (混合整数规划问题)求解如下的混合整数规划问题
m i n min min z = − 3 x 1 − 2 x 2 − x 3 z=-3x_1-2x_2-x_3 z=−3x1−2x2−x3,
s . t . = { x 1 + x 2 + x 3 ≤ 7 , 4 x 1 + 2 x 2 + x 3 = 12 , x 1 , x 2 ≥ 0 , x 3 = 0 或 1 。 s.t.=\begin{cases}x_1+x_2+x_3\leq7,\\4x_1+2x_2+x_3=12,\\x_1,x_2\geq0,\\x_3=0或1。\end{cases} s.t.=⎩ ⎨ ⎧x1+x2+x3≤7,4x1+2x2+x3=12,x1,x2≥0,x3=0或1。
答案:求得的最优解为 x 1 = 0 x_1=0 x1=0, x 2 = 5.5 x_2=5.5 x2=5.5, x 3 = 1 x_3=1 x3=1,最优值为 z = − 12 z=-12 z=−12。
求解的Matlab程序为:
clc,clear
c=[-3;-2;-1];intcon=3; % 整数变量的地址
a=ones(1,3);b=7;
aeq=[4 2 1];beq=12;
lb=zeros(3,1);ub=[inf;inf;1]; % x(3)为0-1变量
x=intlinprog(c,intcon,a,b,aeq,beq,lb,ub)
例1.10 (蒙特卡洛法)已知非线性整数规划为
m a x max max z = x 1 2 + x 2 2 + 3 x 3 2 + 4 x 4 2 + 2 x 5 2 − 8 x 1 − 2 x 2 − 3 x 3 − x 4 − 2 x 5 z={x_1}^2+{x_2}^2+3{x_3}^2+4{x_4}^2+2{x_5}^2-8x_1-2x_2-3x_3-x_4-2x_5 z=x12+x22+3x32+4x42+2x52−8x1−2x2−3x3−x4−2x5
s . t . = { 0 ≤ x i ≤ 99 , i = 1 , … , 5 , x 1 + x 2 + x 3 + x 4 + x 5 ≤ 400 , x 1 + 2 x 2 + 2 x 3 + x 4 + 6 x 5 ≤ 800 , 2 x 1 + x 2 + 6 x 3 ≤ 200 , x 3 + x 4 + 5 x 5 ≤ 200 。 s.t.=\begin{cases}0\leq{x_i}\leq99,i=1,…,5,\\x_1+x_2+x_3+x_4+x_5\leq400,\\x_1+2x_2+2x_3+x_4+6x_5\leq800,\\2x_1+x_2+6x_3\leq200,\\x_3+x_4+5x_5\leq200。\end{cases} s.t.=⎩ ⎨ ⎧0≤xi≤99,i=1,…,5,x1+x2+x3+x4+x5≤400,x1+2x2+2x3+x4+6x5≤800,2x1+x2+6x3≤200,x3+x4+5x5≤200。
解:如果用显枚举法试探,则共需计算 ( 100 ) 5 = 1 0 10 (100)^5=10^{10} (100)5=1010个点,其计算量非常之大。然而应用蒙特卡洛去随机计算106个点,便可找到满意解,那么这种方法的可信度究竟怎样呢?下面就随机取样采集106个点计算,应用概率理论来估计一下可信度。
不失一般性,假定一个整数规划的最优点不是孤立的奇点。
假设目标函数落在高值区的概率分别为0. 01、0. 00001,则当计算106个点后,至少有一个点能落在高值区的概率分别为1-0. 991000000≈0. 99···99(100多位),1-0.999991000000≈0.999954602。
答案:使用Lingo求得的全局最优解为 x 1 = 50 x_1=50 x1=50, x 2 = 99 x_2=99 x2=99, x 3 = 0 x_3=0 x3=0, x 4 = 99 x_4=99 x4=99, x 5 = 20 x_5=20 x5=20,最优值为 z = 52368 z=52368 z=52368;使用Matlab求得的因为是随机模拟,所以每次的运行结果都是不一样的。
(1)首先编写M文件mente.m定义目标函数f和约束向量函数g,程序如下:
function[f,g]=mengte(x);
f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)-3*x(3)-x(4)-2*x(5);
g=[sum(x)-400
x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
2*x(1)+x(2)+6*x(3)-200
x(3)+x(4)+5*x(5)-200];
(2)求解的Matlab程序为:
rand('state',sum(clock)); % 初始化随机数发生器
p0=0;
tic % 计时开始
for i=1:10^6
x=randi([0,99],1,5); % 产生一行五列的区间[0,99]上的随机整数
[f,g]=mengte(x);
if all(g<=0)
if p0<f
x0=x;p0=f; % 记录下当前较好的解
end
end
end
x0,p0
toc % 计时结束
(3)求解的Lingo程序为:
model:
sets:
row/1..4/:b;
col/1..5/:c1,c2,x;
link(row,col):a;
endsets
data:
c1=1,1,3,4,2;
c2=--8,-2,-3,-1,-2;
a=1 1 1 1 1
1 2 2 1 6
2 1 6 0 0
0 0 1 1 5;
b=400,800,200,200;
enddata
max=@ sum(col:c1*x^2+c2*x);
@ for(row(i):@ sum(col(j):a(i,j)*x(j))<b(i));
@ for(col:@ gin(x));
@ for(col:@ bnd(0,x,99));
end