⌈C语言⌋ 用队列实现二叉树的层序遍历（广度优先搜索）

目录

一、 前言

二、 用队列实现二叉树层序遍历

1. 为何使用队列？

3. 解题模板

4. 手动实现队列的相关函数

5. 用数组模拟队列

三、 实战演练

---

一、 前言

在之前的文章中我们学习过二叉树的前、中、后三种遍历顺序，使用递归可以说是相当的简单（当然大家也可以尝试一下用迭代法实现一下这三种遍历）；

这篇文章我们一起来学习一下二叉树的层序遍历；

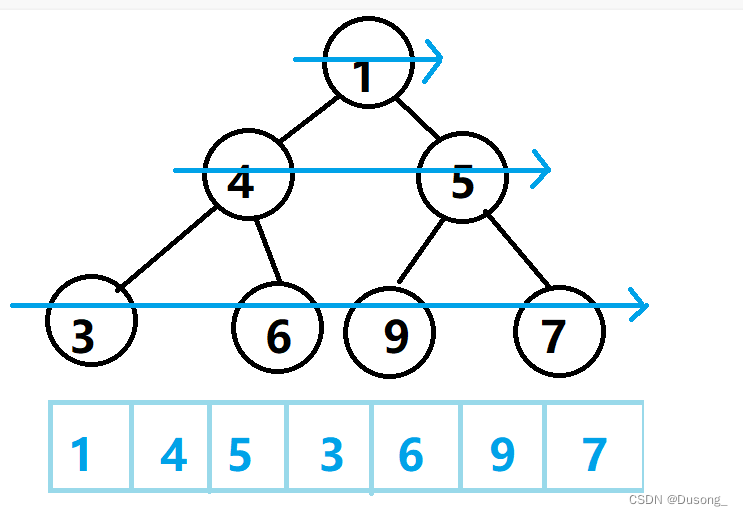
什么是层序遍历？

废话短说，就是一层一层地遍历二叉树，至于如何遍历呢，我们紧接着就来讲解。

二、 用队列实现二叉树层序遍历

关于二叉树的层序遍历，leetcode上也有专门一道题，大家可以结和那道题，学会之后再去做做

102. 二叉树的层序遍历➡️https://leetcode.cn/problems/binary-tree-level-order-traversal/

1. 为何使用队列？

为什么不能用递归：

不同于前、中、后序遍历，如果想用递归实现层序遍历，那么可以想象，一个结点递归左右子树到达第下一层，那么同一层地需要往回递归，这时很难实现地；

为什么使用队列：

所以我们需要借助队列这一数据结构来实现队列https://blog.csdn.net/Dusong_/article/details/127061544?spm=1001.2014.3001.5502

 队列地特性是先进先出，

每读取一个队列中的结点，就将该结点地左右子结点加入队列中，所以每当遍历完一层之后，队列里就有下一层的地所有结点了；

那么如何知道每一层有多少个结点呢？我们都知道取完一层结点之后下一层的结点就在队列中了，那么在遍历一层之前调用QueueSize函数得到队列地中的结点数量，再用一层while（size--）就解决问题了

3. 解题模板

这里我们用类似于C语言地伪代码，方便理解

    Queue q;
    //初始化队列

    if(root){
        QueuePush(&q,root);
    }
    while(!QueueEmpty(&q)){
        //注意size需要提前记录用于while循环，因为队列地结点个数随时都在改变
        int size = QueueSize(&q);  

        while(size--){

            struct TreeNode* node = QueueFront(&q);  //取队首结点

            QueuePop(&q);  //弹出队首结点

            T_res[tresTop][fresTop++] = node -> val;   //收集结点值
            //将该结点地左右结点存放入队列中
            if(node -> left){
                QueuePush(&q, node -> left);
            }

            if(node -> right){
                QueuePush(&q, node -> right);
            }
        }

4. 手动实现队列的相关函数

手动实现队列的函数，对比C++的代码，C语言用“纯队列”确实有点小题大做了

typedef struct QueueNode{
	struct QueueNode* next;
	struct TreeNode* data;
}QNode;
typedef struct Queue{
	QNode* head;
	QNode* tail;
}Queue;

void QueuePush(Queue* pq, struct TreeNode* treenode){
    QNode* newnode = (QNode*)malloc(sizeof(QNode));
    newnode -> data = treenode;
    newnode -> next = NULL;

	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;

	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = pq->tail->next;
	}
}

void QueuePop(Queue* pq){
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

struct TreeNode* QueueFront(Queue* pq){
	return pq->head->data;
}

int QueueSize(Queue* pq){
	int size = 0;
	QNode* cur = pq->head;
	while (cur != NULL)
	{
		size++;
		cur = cur->next;
	}
	return size;
}

bool QueueEmpty(Queue* pq){
	return pq->head == NULL;
}
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
    int** T_res = (int**)malloc(sizeof(int*)*2000);
    int* fSize = (int*)malloc(sizeof(int)*2000);
    int tresTop = 0;
    Queue q;
    q.head = q.tail = NULL;

    if(root){
        QueuePush(&q,root);
    }
    while(!QueueEmpty(&q)){
        int fresTop = 0;   //记录一层收集地结点数
        int size = QueueSize(&q);
        T_res[tresTop] = (int*)malloc(sizeof(int) * size);    //结果集

        while(size--){
            struct TreeNode* node = QueueFront(&q);
            QueuePop(&q);

            T_res[tresTop][fresTop++] = node -> val;

            if(node -> left){
                QueuePush(&q, node -> left);
            }
            if(node -> right){
                QueuePush(&q, node -> right);
            }
        }
        fSize[tresTop++] = fresTop;   //colmunSize
    }

    *returnSize = tresTop;
    *returnColumnSizes = fSize;
    return T_res;
}

5. 用数组模拟队列

所以我们考虑一下用数组模拟栈，省去手动实现队列的相关函数过程：

int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
    if(root == NULL){
    *returnSize = 0;
    return NULL;
}

    int** T_res = (int**)malloc(sizeof(int*)*2000);  //结果集
    int* fSize = (int*)malloc(sizeof(int)*2000);   //每层结果数
    int tresTop = 0; 
    
    struct TreeNode* que[2000];   //用数组模拟队列实现
    memset(que,0,sizeof(que));

    int head = 0;  //控制队首
    int tail = 0;   //控制队尾
    que[tail++] = root;

    while(head < tail){
        int fresTop = 0;
        int size = tail - head;
        T_res[tresTop] = (int*)malloc(sizeof(int)*size);

        while(size--){
            struct TreeNode* node = que[head++];
            T_res[tresTop][fresTop++] = node -> val;

            if(node -> left){
                que[tail++] = node -> left;
            }
            if(node -> right){
                que[tail++] = node -> right;
            }
        }
        fSize[tresTop++] = fresTop;
    }

    *returnSize = tresTop;
    *returnColumnSizes = fSize;
    return T_res;
}

三、 实战演练

513. 找树左下角的值➡️https://leetcode.cn/problems/find-bottom-left-tree-value/

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 :

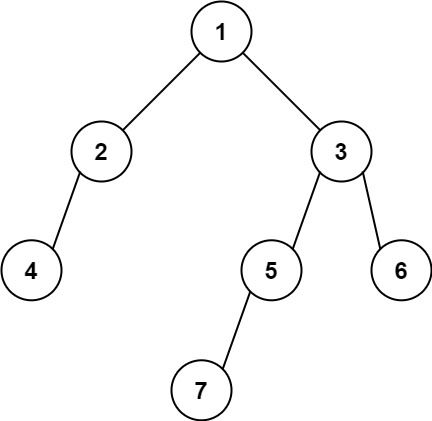
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

这道题的解法很简单，可以套用之前说过的解题模板，加上一些细微的改变，这里我就直接将代码放在这里，有兴趣的同学可以子集尝试做一做✔️ 

int findBottomLeftValue(struct TreeNode* root){
    struct TreeNode* que[100000];   
    memset(que,0,sizeof(que));
    int head = 0;  
    int tail = 0;   

    que[tail++] = root;  //先将根节点加入队列中

    int BottomLeft;   //记录每一层最左边的结点值

    while(head < tail){
        int size = tail - head;
        for(int i = 0; i < size; i++){   
            struct TreeNode* node = que[head++];   //取队首结点

            if(i == 0){  
                BottomLeft = node -> val;    //i == 0时即取出的结点为每一层的第一个结点
            }
            if(node -> left){
                que[tail++] = node -> left;
            }
            if(node -> right){
                que[tail++] = node -> right;
            }
        }

    }
    return BottomLeft;
}