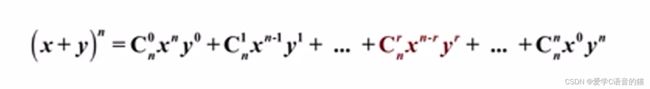C语言基础:杨辉三角
杨辉三角简介:
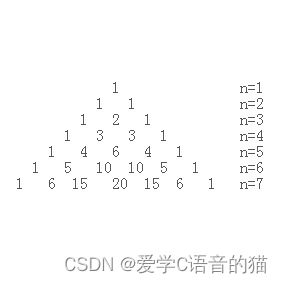
杨辉三角,是二项式系数在三角形中的一种几何排列,中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡(1623----1662)在1654年发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。杨辉三角是中国数学史上的一个伟大成就。
二项式定理:
杨辉三角是二项式(x+y)^n展开后各项的系数。
比如:
(a+b)^0展开后是为1,系数为1;
(a+b)^1展开后是为a+b,系数为1,1;
(a+b)^2展开后是为a^2+2ab+b^2,系数为1,2,1;
(a+b)^3展开后是为a^3+3a^2b+3ab^2+b^3,系数为1,3,3,1;
(a+b)^4展开后是为a^4+4a^3b+6a^2b^2+4ab^3+b^4,系数为1,4,6,4,1;
.............
打印杨辉三角:
1.1:找规律:
杨辉三角各行的系数有如下规律:
(1):各行的第一个数是1,最后一个数也是一。
(2):每一行的个数等于该行行数 。
(3):从第三行起。除第一个数和最后一个数外,中间的数都是等于它上一行前一列的数和上一行本列数之和。
1.2:根据规律一步一步实现:
1.2.1 实现各行的第一个数是1,最后一个数也是一:
#include
#define N 10
int main()
{
int arr[N][N] = { 0 }; //要先初始化
int i = 0;//行数
int j = 0;//列数
for (i = 0; i < N; i++)
{
arr[i][0] = 1; //每行首元素是 1
for (j = 0; j <= i; j++)//为啥j<=i呢?因为每一行的个数(每一列多少个=j)
//等于该行行数 (i)
{
if (i == j)
arr[i][j] = 1; //每行末位是 1
}
}
//打印出来看看上面写的对不对
for (i = 0; i < N; i++)
{
for (j = 0; j <= i; j++)
{
printf("%d ", arr[i][j]);
}
printf("\n");
}
return 0;
} 调试结果如下:
当然,现在还只是直角三角形的形式,后面我们会插入空格形成等腰三角形的形式。
1.2.2:处理中间元素 :
根据规律(3):从第三行起。除第一个数和最后一个数外,中间的数都是等于它上一行前一列的数和上一行本列数之和。我们可以怎么写成代码形式呢?
我们先举例子:
第4行第2个数(3)=第3行第2个数(2)+第3行第一个数(1);
i表示行,j表示列,是不是i>=2时(i从0开始的)表示从第三行起:
有 arr[ i ][ j ]=arr[ i-1 ][ j ]+arr[ i-1 ][ j-1 ]
#define N 10
int main()
{
int arr[N][N] = { 0 }; //要先初始化
int i = 0;//行数
int j = 0;//列数
for (i = 0; i < N; i++)
{
arr[i][0] = 1; //每行首元素是 1
for (j = 0; j <= i; j++)//为啥j<=i呢?因为每一行的个数(每一列多少个=j)等于该行行数 (i)
{
if (i == j)
{
arr[i][j] = 1; //每行末位是 1
}
if (i >= 2 && j >= 1) //中间元素在第三行第二列才开始有,
//之后每一行的中间元素都要执行。
{
arr[i][j] = arr[i - 1][j] + arr[i - 1][j-1];
}
}
}
//打印
for (i = 0; i < N; i++)
{
for (j = 0; j <= i; j++)
{
printf("%d ", arr[i][j]);
}
printf("\n");
}
return 0;
}调试结果如下:
1.3代码精简化:
当然,打印上面一幅图方法有很多啊,比如上面写的代码,最后打印时其实可以在复值完每一行后直接打印这一行的数据,再加个换行符。自己对比一下。
#define N 10
int main()
{
int arr[N][N] = { 0 }; //要先初始化
int i = 0;//行数
int j = 0;//列数
for (i = 0; i < N; i++)
{
arr[i][0] = 1; //每行首元素是 1
for (j = 0; j <= i; j++)//为啥j<=i呢?因为每一行的个数(每一列多少个=j)等于该行行数 (i)
{
if (i == j)
{
arr[i][j] = 1; //每行末位是 1
}
if (i >= 2 && j >= 1) //中间元素在第三行第二列才开始有,之后每一行的中间元素都要执行。
{
arr[i][j] = arr[i - 1][j] + arr[i - 1][j-1];
}
printf("%6d", arr[i][j]);//直接打印这一行数据
}
printf("\n");
}
return 0;
}其实在给各行第一个数和最后一个数赋值为1时,可以只用到一个循环 。不需要两个for循环的,函数和列数是相同的,上面的代码是不是要判断if (i == j),i最后和j是相同的。
下面这段代码也是打印杨辉三角的。
#define N 10
int main()
{
int a[N][N];
int i, j;
for (i = 0; i < N; i++)
{
a[i][i] = 1;//使对角线元素为1;(每一行最后一个元素)
a[i][0] = 1;//第一列元素为1
}
for (i = 2; i < N; i++)//从第三行开始
{
for (j = 1; j <= i - 1; j++)//第三行中间元素是第二列开始,j<=i-1;
//中间元素就是从2列到i-1列的
{
a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
}
}
//打印
for (i = 0; i < N; i++)
{
for (j = 0; j <= i; j++)
{
printf("%d ", a[i][j]);
}
printf("\n");
}
return 0;
}1.4:打印等腰三角形的杨辉三角:
我们已经得到了如图所示的杨辉三角,想要变成等腰三角形形式只需要在每行打印空格就OK了。
比如我们先把前五行打印好:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | ||||||||||||||||||
| 1 | 2 | 1 | |||||||||||||||||
| 1 | 3 | 3 | 1 | ||||||||||||||||
| 1 | 4 | 6 | 5 | 1 | |||||||||||||||
首先我们看最后一行出现了三位数,三位数要占三个字符,所以我们打印使直接分配三个空间,%-3d,左对齐,输出的数字占三个字符的位置。%-3d不理解的话我直接看代码加图吧
int main()
{
int a = 1;
int b = 11;
int c = 111;
printf("0%-3d0\n", a);
printf("0%-3d0\n", b);
printf("0%-3d0", c);
return 0;
}| 0 | 1 | 空格 | 空格 | 0 |
| 0 | 1 | 1 | 空格 | 0 |
| 0 | 1 | 1 | 1 | 0 |
输出结果就是表格中的一样,左对齐,占三个字符,自己验证一下。
b = 10 - i;
while (b--)
{
printf(" ");
}
比如我们以上面代码形式输入空格,i表示行,i=0时,b=10,10次循环,一次循环输出两个空格,i++,第二行就是2*9个空格,依次计算,最后i=9,输出两个空格
为了输出如上所示的等腰三角形。首先是不是要确保第一个元素在最中间的位置,所以我们先算一算最后一行占了多少个字符空间。
每个元素占三个字符空间,打印一个元素后要加一个空格来保持元素之间不要太密。四个字符空间,第一个元素又打印了两个字符,2+10*4=42;
所以第一个元素要放在42/2=21的位置。第一个元素刚好前面打印20个空格就OK了
代码如下:
#define N 10
int main()
{
int arr[N][N] = { 0 }; //要先初始化
int i = 0;//行数
int j = 0;//列数
int b = 0;
for (i = 0; i < N; i++)
{
arr[i][0] = 1; //每行首元素是 1
b = 10 - i;
while (b--)
{
printf(" ");
}
for (j = 0; j <= i; j++)//为啥j<=i呢?因为每一行的个数(每一列多少个=j)等于该行行数 (i)
{
if (i == j)
{
arr[i][j] = 1; //每行末位是 1
}
if (i >= 2 && j >= 1) //中间元素在第三行第二列才开始有,之后每一行的中间元素都要执行。
{
arr[i][j] = arr[i - 1][j] + arr[i - 1][j-1];
}
printf("%-3d ", arr[i][j]);//直接打印这一行数据
}
printf("\n");
}
return 0;
}
调试结果如下: