算法小抄8--链表
定义
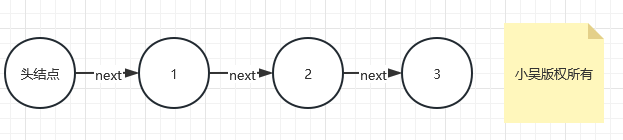
链表(指单链表)是一个由头部节点引导的,通过节点指针连接在一起的数据结构,它的形状如下:
链表中的节点代码定义如下:
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next相对于线性表,链表的优势在于快速的插入和删除中间的元素(这里要说明的是,如果是对于尾部元素的插入与删除,线性表其实比链表要快),两者的删除操作如下图所示:
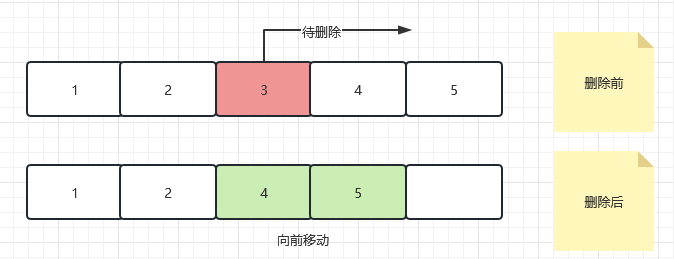
顺序表删除:
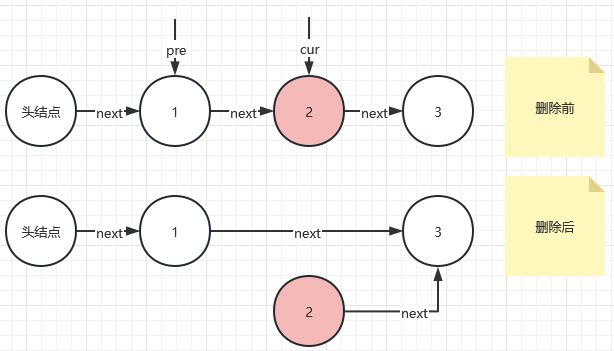
链表删除:
是不是发现链表删除以后2的next仍然指向3,看起来和链表内部似乎还有联系?但是从逻辑上我们已经无法通过遍历的方式在链表中查找到2了,所以2已经算是被删除了
链表的基本操作
遍历操作
head为链表的头节点
cur=head //我们创建一个cur引用指向头节点
//只要链表当前值不为空
while (cur!=null){
//具体操作
...
//移动cur指针
cur=cur.next
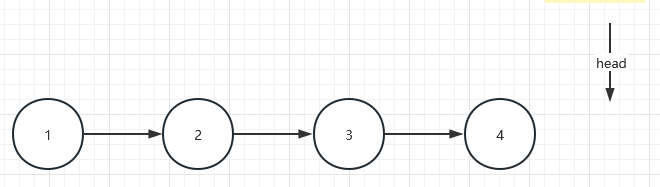
}可以看到,我们这里创建了一个cur引用指向了head,为什么不直接使用head进行遍历呢?对于一个存储1,2,3,4的链表,它的形状如下,head指针最开始是指向1的
如果我们直接使用head指针进行遍历操作,遍历操作完以后链表情况如下,我们发现head指向了空节点,如果我们还想对当前链表进行遍历操作怎么办呢?此时已经无法从头开始遍历查找了,因为head已经指向了空
而如果使用cur指针,我们遍历完以后,链表的形状是这样的,这次是cur指向空,而head依旧还指向头节点,我们依然可以进行遍历操作:
删除某个节点
删除某个节点我们在上面已经画过图了,这里直接贴下来,其实一行代码就可以达到一下的效果,pre.next=cur.next, 删除的对象是2,pre代表删除对象的前一个对象,是不是被这些next绕晕了,我们来分析一下, =号左边是进行赋值的域,也就是我们要对pre的next指针进行赋值操作,在这个例子中我们要对1的next进行赋值操作,而=号的右边是要附上的值,cur.next代表的是3这个节点
所以我们需要先找到待删除节点的前一个节点,其实我们也不需要用到cur指针,而是采用pre.next来代替cur指针的使用,代码如下:
cur = head
//注意看循环条件,因为我们在循环中使用了cur.next
//为了避免空指针异常,while条件中也不能写cur!=null
while(cur.next!=null){
//cur.next为目标删除节点,那么cur是否就是pre了
if(cur.next==target){
//注意看这里cur现在是pre
//等号右边的cur.next是否就是我们分析的cur
//这个代码是否就等价于pre.next=cur.next
cur.next=cur.next.next
}
cur=cur.next
}思考一下,如果链表过短的话,cur.next.next操作是否会引发空指针呢?
答案是不会哈,空指针异常的发生条件是当一个对象本来就是空,我们还要继续访问它的一些属性,也就是我们访问了null.null才会导致空指针,而我们的循环条件是cur,next!=null,这就保证了我们至少访问的是value.null,这个操作时不会导致空指针滴
插入某个节点
插入节点与删除某个节点类似都需要找到待操作位置的前一个节点,其伪代码如下:
定义insert为待插入节点
pre为插入位置的前置节点
insert.next=pre.next
pre.next=insert
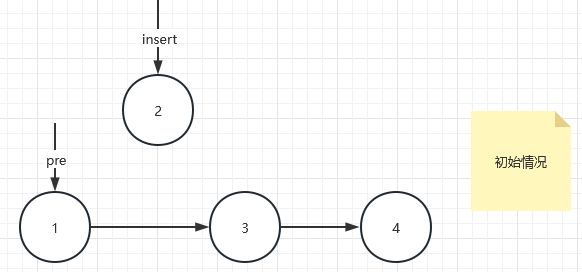
思考一下这两行代码能否反过来写呢?答案是不行的嗷,例子如下对于1,3,4这个链表,如果我们要在中间插入2这个节点,若先执行pre.next=insert会发生什么呢?
先执行pre.next=insert语句,=号左边对1节点的next域进行赋值, 即1.next=2
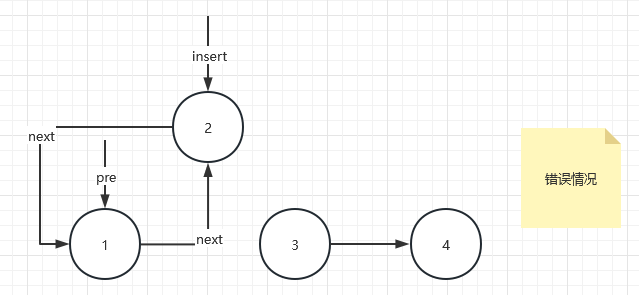
而后执行insert.next=pre.next语句,pre依旧指向1,我们要对2.next这个域进行赋值,本来进行插入操作insert.next应该被赋值为3才对,而现在由于pre.next被我们覆盖替换为了1,导致了2.next=1,形成了链表环路
基础操作熟悉了,现在就要开始上强度了,看看链表题有什么骚操作吧
题一:反转链表
题目链接
我们先理一下思路,看看怎么操作才能把整个链表反过来,用画图来表示的话应该是这样式的:
反转链表:
pre cur next
1 -> 2 -> 3 -> 4 -> 5
pre cur next
1 <- 2 3 -> 4 -> 5
pre cur next
1 <- 2 <- 3 4 -> 5
pre cur next
1 <- 2 <- 3 <- 4 5
pre cur next
1 <- 2 <- 3 <- 4 <- 5
pre cur next
1 <- 2 <- 3 <- 4 <- 5
试着根据这个图来还原一下代码吧:
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
pre, cur = None, head
while cur:
nxt = cur.next # 记录当前节点的下一个节点
cur.next = pre # 然后将当前节点指向pre
pre = cur # pre和cur节点都前进一位
cur = nxt
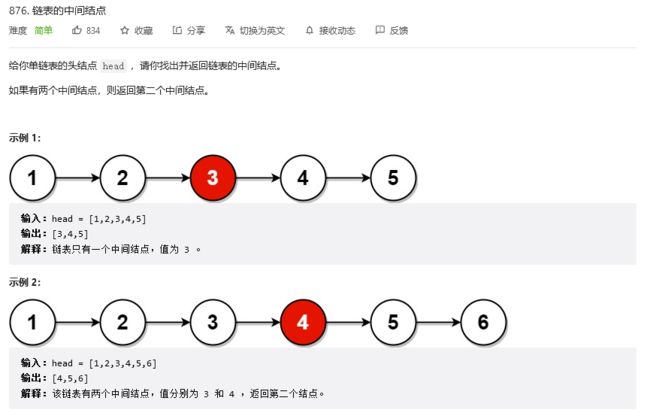
return pre题二:寻找链表的中点
题目链接
第一种简单的思路是,先通过遍历一次,找到链表有多少个节点,然后再遍历一次找到链表的中点进行返回,其代码如下:
class Solution:
def middleNode(self, head: ListNode) -> ListNode:
n, cur = 0, head
"""第一次遍历"""
while cur:
n += 1
cur = cur.next
"""第二次遍历"""
k, cur = 0, head
while k < n // 2:
k += 1
cur = cur.next
return cur第二种思路比较难想到啦,但是是必须要掌握的一个方法,我们运用两个指针slow和fast,slow每次走一步,fast每次走两步,当fast走到结尾的时候,slow是否就刚好到了中点的位置呢?通过这个方法我们可以通过一次遍历就找到链表的中点
class Solution:
def middleNode(self, head: ListNode) -> ListNode:
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow注意注意:
这里对于偶数我们返回的是两个节点中的后一个节点,循环里写的条件是fast and fast.next不为空,如果我们要返回两个节点中的前一个节点循环条件该如何写呢?
答案是 while fast.next and fast.next.next 羊羊可以自己举个例子还原一下
题三:检查回文链表
题一和题二都是链表题中必须掌握的操作哦,因为有时他们还能打出梦幻的combo,比如下面这题:
题目链接
回文是力扣题的一个常用概念,例如12344321这样的对称的数被称为回文的数字串,那么如何检查一个链表是否是回文链表呢,先思考一下,如何利用题一和题二来解决
- 题一中我们学会了如何翻转链表,题二中我们学会了找到链表的中点
- 我们先查找到链表的中点,断开链表后,对后续的链表进行翻转操作,然后一个一个对比,是否就能判断该链表是否回文了呢?
- 在判断完之后,链表已经被我们断开并且翻转了,为了链表以后还能正确使用,我们是否应该还原链表呢?
先自己写再看最后的答案哦
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
if head is None:
return True
# 找到前半部分链表的尾节点并反转后半部分链表
first_half_end = self.end_of_first_half(head)
second_half_start = self.reverse_list(first_half_end.next)
# 判断是否回文
result = True
first_position = head
second_position = second_half_start
while result and second_position is not None:
if first_position.val != second_position.val:
result = False
first_position = first_position.next
second_position = second_position.next
# 还原链表并返回结果
first_half_end.next = self.reverse_list(second_half_start)
return result
#找到链表的中点,如果为偶数是找前一个
def end_of_first_half(self, head):
fast = head
slow = head
while fast.next is not None and fast.next.next is not None:
fast = fast.next.next
slow = slow.next
return slow
#翻转链表
def reverse_list(self, head):
previous = None
current = head
while current is not None:
next_node = current.next
current.next = previous
previous = current
current = next_node
return previous