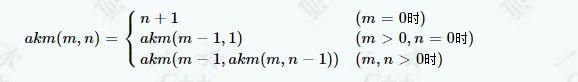2024寒假集训 进阶训练赛 (一)
目录
问题 A: 校门外的树
问题 B: 开关灯
问题 C: 机器翻译
问题 D: 素数对
问题 E: 阿克曼函数
问题 F: 甲流病人初筛
问题 G: 【蓝桥杯2021初赛】空间
问题 H: 【蓝桥杯2021初赛】卡片
问题 I: 回到学校
问题 J: 九九乘法表(教师版)
问题 K: 好人 or 坏人 ?
问题 L: 双刀流银色战车
问题 M: 点外卖
问题 N: 宝藏开箱者
问题 O: 奇异吃牌者
问题 P: 2.4.9.2 双重队列
问题 Q: 第K小乘积
问题 R: 消灭大整数
问题 S: 关灯
问题 T: 计信狗的大一下
问题 A: 校门外的树
题目描述
某校大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴,马路的一端在数轴0的位置,另一端在L的位置;数轴上的每个整数点,即0,1,2,……,L,都种有一棵树。
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。
输入
第一行有两个整数L(1 ≤ L ≤ 10000)和 M(1 ≤ M ≤ 100),L代表马路的长度,M代表区域的数目,L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整数,用一个空格隔开,表示一个区域的起始点和终止点的坐标。
对于20%的数据,区域之间没有重合的部分;对于其它的数据,区域之间有重合的情况。
输出
包括一行,这一行只包含一个整数,表示马路上剩余的树的数目。
样例输入 复制
500 3
150 300
100 200
470 471
样例输出 复制
298AC代码:
#include
using namespace std;
int main()
{
int l, m;
cin >> l >> m;
int a[l + 5];
memset(a, -1, sizeof(a));
for (int i = 0; i < m; i++)
{
int x, y;
cin >> x >> y;
for (int j = x; j <= y; j++)
a[j] = 0;
}
int sum = 0;
for (int i = 0; i <= l; i++)
{
if (a[i])
sum++;
}
cout << sum;
return 0;
} 问题 B: 开关灯
题目描述
假设有N盏灯(N为不大于5000的正整数),从1到N按顺序依次编号,初始时全部处于开启状态;有M个人(M为不大于N的正整数)也从1到M依次编号。
第一个人(1号)将灯全部关闭,第二个人(2号)将编号为2的倍数的灯打开,第三个人(3号)将编号为3的倍数的灯做相反处理(即将打开的灯关闭,将关闭的灯打开)。依照编号递增顺序,以后的人都和3号一样,将凡是自己编号倍数的灯做相反处理。
请问:当第M个人操作之后,哪几盏灯是关闭的,按从小到大输出其编号,其间用逗号间隔。
输入
输入正整数N和M,以单个空格隔开。
输出
顺次输出关闭的灯的编号,其间用逗号间隔。
样例输入 复制
10 10样例输出 复制
1,4,9AC代码:
#include
using namespace std;
int main()
{
int n, m;
cin >> n >> m;
int a[n + 5];
memset(a, 0, sizeof(a));
for (int i = 2; i <= m; i++)
{
for (int j = i; j <= n; j += i)
{
a[j] = (a[j] + 1) % 2;
}
}
queue q;
for (int i = 1; i <= n; i++)
{
if (!a[i])
q.push(i);
}
while (!q.empty())
{
cout << q.front();
q.pop();
if (!q.empty())
cout << ",";
}
return 0;
} 问题 C: 机器翻译
题目描述
小晨的电脑上安装了一个机器翻译软件,他经常用这个软件来翻译英语文章。
这个翻译软件的原理很简单,它只是从头到尾,依次将每个英文单词用对应的中文含义来替换。对于每个英文单词,软件会先在内存中查找这个单词的中文含义,如果内存中有,软件就会用它进行翻译;如果内存中没有,软件就会在外存中的词典内查找,查出单词的中文含义然后翻译,并将这个单词和译义放入内存,以备后续的查找和翻译。
假设内存中有M 个单元,每单元能存放一个单词和译义。每当软件将一个新单词存入内存前,如果当前内存中已存入的单词数不超过M−1,软件会将新单词存入一个未使用的内存单元;若内存中已存入M 个单词,软件会清空最早进入内存的那个单词,腾出单元来,存放新单词。
假设一篇英语文章的长度为N 个单词。给定这篇待译文章,翻译软件需要去外存查找多少次词典?假设在翻译开始前,内存中没有任何单词。
输入
共2 行。每行中两个数之间用一个空格隔开。
第一行为两个正整数M 和N,代表内存容量和文章的长度。
第二行为N 个非负整数,按照文章的顺序,每个数(大小不超过1000)代表一个英文
单词。文章中两个单词是同一个单词,当且仅当它们对应的非负整数相同。
【数据范围】
对于10%的数据有M=1,N≤ 5。
对于100%的数据有0 < M≤ 100,0< N ≤ 1000。
输出
共1 行,包含一个整数,为软件需要查词典的次数。
样例输入 复制
3 7
1 2 1 5 4 4 1样例输出 复制
5提示
【输入输出样例 1 说明】
整个查字典过程如下:每行表示一个单词的翻译,冒号前为本次翻译后的内存状况:
空:内存初始状态为空。
1. 1:查找单词1 并调入内存。
2. 1 2:查找单词2 并调入内存。
3. 1 2:在内存中找到单词1。
4. 1 2 5:查找单词5 并调入内存。
5. 2 5 4:查找单词4 并调入内存替代单词1。
6. 2 5 4:在内存中找到单词4。
7. 5 4 1:查找单词1 并调入内存替代单词2。
共计查了5 次词典。
AC代码:
#include
using namespace std;
int main()
{
int m, n;
cin >> m >> n;
int que[n + 5]; // 数组模拟队列
int sum = 0, back = 0, front = 0;
for (int i = 0; i < n; i++)
{
int a; // 待查词
cin >> a;
int flag = 0;
for (int j = front; j < back; j++)
{ // 在内存中查找
if (que[j] == a)
{
flag = 1;
}
}
if (!flag)
{ // 未找到,入队
sum++;
if (back >= m)
front++;
que[back++] = a;
}
}
cout << sum;
return 0;
} 问题 D: 素数对
题目描述
两个相差为2的素数称为素数对,如5和7,17和19等,本题目要求找出所有两个数均不大于n的素数对。
输入
一个正整数n(1≤n≤10000)。
输出
所有小于等于n的素数对。每对素数对输出一行,中间用单个空格隔开。若没有找到任何素数对,输出empty。
样例输入 复制
100
样例输出 复制
3 5
5 7
11 13
17 19
29 31
41 43
59 61
71 73AC代码:
#include
using namespace std;
int isprime(int x)
{
int flag = 1;
for (int i = 2; i <= sqrt(x); i++)
{
if (x % i == 0)
{
flag = 0;
break;
}
}
return flag;
}
int main()
{
int n, flag = 0;
cin >> n;
for (int i = 3; i <= n - 2; i++)
{
if (isprime(i) && isprime(i + 2))
{
cout << i << " " << i + 2 << endl;
flag = 1;
}
}
if (flag == 0)
cout << "empty";
return 0;
} 问题 E: 阿克曼函数
题目描述
阿克曼(Ackmann)函数A(m,n)中,m,n定义域是非负整数(m≤3,n≤10),函数值定义为:
输入
输入m和n。
输出
函数值
样例输入 复制
2 3样例输出 复制
9AC代码:
#include
using namespace std;
int ackmann(int m, int n)
{
if (m == 0)
return n + 1;
if (m > 0 && n == 0)
return ackmann(m - 1, 1);
return ackmann(m - 1, ackmann(m, n - 1));
}
int main()
{
int m, n;
cin >> m >> n;
cout << ackmann(m, n);
return 0;
} 问题 F: 甲流病人初筛
题目描述
目前正是甲流盛行时期,为了更好地进行分流治疗,医院在挂号时要求对病人的体温和咳嗽情况进行检查,对于体温超过37.5度(含等于37.5度)并且咳嗽的病人初步判定为甲流病人(初筛)。现需要统计某天前来挂号就诊的病人中有多少人被初筛为甲流病人。
输入
第一行是某天前来挂号就诊的病人数n。(n<200)
其后有n行,每行是病人的信息,包括三个信息:姓名(字符串,不含空格,最多8个字符)、体温(float)、是否咳嗽(整数,1表示咳嗽,0表示不咳嗽)。每行三个信息之间以一个空格分开。
输出
按输入顺序依次输出所有被筛选为甲流的病人的姓名,每个名字占一行。之后在输出一行,表示被筛选为甲流的病人数量。
样例输入 复制
5
Zhang 38.3 0
Li 37.5 1
Wang 37.1 1
Zhao 39.0 1
Liu 38.2 1样例输出 复制
Li
Zhao
Liu
3AC代码:
#include
using namespace std;
int main()
{
int n, sum = 0;
cin >> n;
while (n--)
{
char s[10];
double tem;
int cough;
cin >> s >> tem >> cough;
if (tem >= 37.5 && cough)
{
sum++;
cout << s << endl;
}
}
cout << sum;
return 0;
} 问题 G: 【蓝桥杯2021初赛】空间
题目描述
小蓝准备用256MB 的内存空间开一个数组,数组的每个元素都是32 位二进制整数。
如果不考虑程序占用的空间和维护内存需要的辅助空间,请问256MB 的空间可以存储多少个32 位二进制整数?
输入
无
输出
无
AC代码:
#include
using namespace std;
int main()
{
cout << "67108864";
return 0;
}
// 32 bit --> 4 byte(B)
// 256*1024^2/4=67108864 问题 H: 【蓝桥杯2021初赛】卡片
题目描述
小蓝有很多数字卡片,每张卡片上都是数字0 到9。
小蓝准备用这些卡片来拼一些数,他想从1 开始拼出正整数,每拼一个,就保存起来,卡片就不能用来拼其它数了。
小蓝想知道自己能从1 拼到多少。
例如,当小蓝有30 张卡片,其中0 到9 各3 张,则小蓝可以拼出1 到10,但是拼11 时卡片1 已经只有一张了,不够拼出11。
现在小蓝手里有0 到9 的卡片各2021 张,共20210 张,请问小蓝可以从1拼到多少?
输入
无
输出
结果
AC代码:
#include
using namespace std;
#define NUM 2021
int main()
{
int card[10];
for (int i = 0; i < 10; i++)
card[i] = NUM;
int flag = 1, m = 1;
while (flag)
{
int k = m;
while (k)
{
card[k % 10]--;
k /= 10;
}
m++;
for (int i = 0; i < 10; i++)
{
if (card[i] <= 0)
{
// cout << card[i] << " ";
flag = 0;
break;
}
}
}
cout << m - 1;
return 0;
} 问题 I: 回到学校
题目描述
愉快的假期总是那么的短暂。
回到学校后,小T监测了教室的进出情况。
假设班级里有 N 个同学,学号分别是 1∼N,小T记录了每位同学分别是第几个进入的教室。
你可以通过上述记录,按进入教室的先后顺序输出同学的学号吗?
输入
N A1 A2 ... AN
第一行一个正整数 N ,代表同学的个数。
第二行有空格隔开的 N 个正整数,A i代表学号为 i的同学是第几个进入教室的。
数据范围:
- 1 ≤ N ≤ 1 0 5 1leq Nleq 10^51≤N≤105
- 1 ≤ A i ≤ N 1leq A_ileq N1≤Ai≤N
- A i ≠ A j ( i ≠ j ) A_i ≠ A_j(i ≠ j)Ai≠Aj(i≠j)
输出
输出一行一个正整数,第 i ii 个整数代表第 i ii 个进入教室的同学的学号。
样例输入 复制
3
2 3 1样例输出 复制
3 1 2AC代码:
#include
using namespace std;
struct node
{
int num, id;
};
int cmp(struct node a, struct node b)
{
return a.id < b.id;
}
int main()
{
int n;
cin >> n;
struct node a[n];
for (int i = 0; i < n; i++)
{
cin >> a[i].id;
a[i].num = i + 1;
}
sort(a, a + n, cmp);
for (int i = 0; i < n; i++)
cout << a[i].num << " ";
return 0;
} 问题 J: 九九乘法表(教师版)
题目描述
你是XSY的老师,XSY只学过九九乘法表,你看到他的作业中出现了一个数n。
如果这个数在九九乘法表是找不到的,那么他肯定答错了,就输出"No"(不含引号),否则,就输出"Yes"(不含引号)
输入
一个整数 n
代表XSY的答案。 (1≤n≤100)
输出
输出 Yes 或 No
样例输入 复制
10样例输出 复制
Yes样例1解释:因为“二五一十”,可以算出10这个数
AC代码:
#include
using namespace std;
int main()
{
int n;
cin >> n;
int a[105];
memset(a, 0, sizeof(a));
for (int i = 1; i < 10; i++)
{
for (int j = i; j <= 9 * i; j += i)
{
a[j] = 1;
}
}
if (a[n])
cout << "Yes";
else
cout << "No";
return 0;
} 问题 K: 好人 or 坏人 ?
题目描述
有n个人在玩一个游戏,
这个游戏是这样的,我们将n个人分为好人和坏人,也有可能n个人都是好人或者都是坏人
好人说的话一定是对的,坏人说的话有可能对,也有可能不对。
现在给你每个人对另外一些人的判断,
问好人最多有多少个
输入
输出
好人最多有多少个
样例输入 复制
3
1
2 1
1
1 1
1
2 0
样例输出 复制
2AC代码:
int main(){//二进制状态压缩
int a[16][16]={0};
int n;
cin>>n;
for(int i=0;i>m;
for(int j=0;j>a1>>b1;
if(b1==1)
{
a[i][a1-1]=1;
}
else a[i][a1-1]=0;
}
}
int sum=0;
for(int i=1;i< 1<>j &1)
{
if((i>>k&1)!=a[j][k])
{
flag=false;
break;
}
}
}
}
if(flag)
{
int cent=0;
for(int j=0;j>j&1;
}
sum=max(sum,cent);
}
}
cout< 问题 L: 双刀流银色战车
题目描述
银色战车+阿努比斯神是波波仅有的高光时刻,那么波鲁纳雷夫玩节奏光剑的话会怎么样呢?
给出两个长度均为n字符串,L表示所有的左手键需要砍的字符,R表示所有的右手键需要砍的字符。
波波挥剑时遵循左-右-左-右……的顺序。
那么字符出现的顺序应该如何?
输入
1≤n≤100
|L|==|R|==n
输出
总的字符串
样例输入 复制
2
ip cc样例输出 复制
icpcAC代码:
#include
using namespace std;
int main()
{
int n;
cin >> n;
string l, r;
cin >> l >> r;
for (int i = 0; i < n; i++)
{
cout << l[i] << r[i];
}
return 0;
} 问题 M: 点外卖
题目描述
小L和朋友们想趁着疯狂星期八薅羊毛。
他们一共点了n样,每样的价钱是Ai(1≤i≤n)。
疯狂星期八的优惠措施是这样的:店家会给你m张优惠劵,优惠券的作用是将某样的价格打对折(下取整),并且它是可以叠加的。
那么小L他们最少需要多少钱。
输入
n道菜,m张券,第i道菜的价格是x。
1≤n,m≤105
1≤x≤109
输出
最少要花多少钱
样例输入 复制
4 4
1 9 3 5
样例输出 复制
6AC代码:
#include
using namespace std;
typedef long long ll;
int main()
{ // 优先队列
int m, n;
cin >> n >> m;
priority_queue q;
ll sum = 0;
for (int i = 0; i < n; i++)
{
ll a;
cin >> a;
q.push(a);
sum += a;
}
while (m--)
{
int a = q.top();
sum -= (a - a / 2);
q.pop();
q.push(a / 2);
}
cout << sum;
return 0;
} 问题 N: 宝藏开箱者
题目描述
输入
输出
输出一行一个正整数,代表解锁所有的箱子至少花费的金额。若无解输出-1。
样例输入 复制
2 3
10 1
1
15 1
2
30 2
1 2样例输出 复制
25AC代码:
#include
using namespace std;
#define mem(a) memset(a, 0, sizeof(a))
#define dbg(x) cout << #x << " = " << x << endl
#define fi(i, l, r) for (int i = l; i < r; i++)
#define cd(a) scanf("%d", &a)
typedef long long ll;
int dp[1 << 12];
vector keys[1000];
int money[1000];
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < (1 << n); i++)
dp[i] = 1e9;
dp[0] = 0;
for (int i = 0; i < m; i++) {
int a, b;
scanf ("%d%d", &a, &b);
money[i] = a;
for (int j = 0; j < b; j++) {
int t;
scanf("%d", &t);
t--; // 把输入的宝箱号[1,n]映射成方便状态压缩的[0,n-1]
keys[i].push_back(t);
}
}
for (int item = 0; item < m; item++) {
int thisState = 0;
for (int t : keys[item]) {
thisState |= (1 << t);
}
for (int nowState = 0; nowState < (1 << n); nowState++) {
int toState = nowState | thisState;
dp[toState] = min(dp[toState], dp[nowState] + money[item]);
}
}
cout << (dp[(1 << n) - 1] == 1e9 ? -1 : dp[(1 << n) - 1]) << endl;
return 0;
}
好孩子从不撒谎,这道题是Ctrl+C:
Tisfy:https://letmefly.blog.csdn.net/article/details/123415471
问题 O: 奇异吃牌者
题目描述
有一个性格奇异的人,喜欢吃掉不同的扑克牌
初始时共有 N NN 张牌,第 i ii 张牌上的数字是 A i A_iAi。
此人将会选择一个整数 K KK,然后不断重复以下过程:
- 选择 K KK 张数字不同的牌吃掉(吃掉后牌会消失)
直到没法再吃为止。
对于 K = 1 , 2 , . . . N K=1,2,...NK=1,2,...N,分别求出此人最多能够吃几次牌。
输入
N A1 A2 ... AN
数据范围:
-
1 ≤ N ≤ 3 × 1 0 5 1leq Nleq 3 imes10^{5}1≤N≤3×105
-
1 ≤ A i ≤ N 1leq A_ileq N1≤Ai≤N
-
所有输入的数都是整数
输出
输出 N NN 行 N NN 个正整数,第 i ii 行代表 K = i K=iK=i 时,此人最多吃牌几次(每次吃掉K KK张不同的牌)。
样例输入 复制
3
2 1 2样例输出 复制
3
1
0AC代码:
#include
using namespace std;
#define mem(a) memset(a, 0, sizeof(a))
#define dbg(x) cout << #x << " = " << x << endl
#define fi(i, l, r) for (int i = l; i < r; i++)
#define cd(a) scanf("%d", &a)
typedef long long ll;
int a[300010];
int c[300010];
int d[300010];
int main(){
int n;
cin >> n;
for (int i = 1;i <= n; i++){
int x;
cd(x);
a[x]++;
c[a[x]]++;
}
d[0] = 0;
for (int i = 1; i <= n; i++)
d[i] = d[i - 1] + c[i];
for (int k = 1;k <= n; k++) {
int ans = 0;
int left = 0, right = n;
while (left <= right) {
int mid = (left + right) / 2;
if((ll)k * mid <= d[mid]) {
left = mid + 1;
ans = max(ans, mid);
}
else{
right = mid - 1;
}
}
printf("%lld\n", ans);
}
return 0;
}
好孩子从不撒谎,这道题是Ctrl+C:
Tisfy:https://letmefly.blog.csdn.net/article/details/123415480
问题 P: 2.4.9.2 双重队列
题目描述
银行的每个客户都有一个正整数标识K,到银行请求服务时将收到一个正整数优先级P。
银行经理提议打破传统,有时为优先级最低的客户服务,而不是为优先级最高的客户服务。系统将收到以下类型的请求:
0:系统需要停止服务。
1 K P:将客户K及其优先级P添加到等待队列中。
2:为优先级最高的客户提供服务,并将其从等待名单中删除。
3:为优先级最低的客户提供服务,并将其从等待名单中删除。
输入
输入的每一行都包含一个请求,只有最后一行包含停止请求(代码0)。假设在列表中包含新客户的请求时(代码1),在列表中没有统一客户的其他服务请求或有相同的优先级。标识符K小于10的6次方,优先级P小于10的7次方。客户可以多次到银行请求服务,并且每次都可以获得不同的优先级。
输出
对于代码2或3的每个请求,都单行输出所服务客户的标识符。如果请求时等待列表为空,则输出0.
样例输入 复制
2
1 20 14
1 30 3
2
1 10 99
3
2
2
0
样例输出 复制
0
20
30
10
0AC代码:
#include
using namespace std;
typedef long long ll;
int main()
{
int n;
map mp;
while (scanf("%d", &n) && n)
{
if (n == 1)
{
ll a, b;
scanf("%lld%lld", &a, &b);
mp[b] = a;
}
else if (mp.empty())
printf("0\n");
else if (n == 3)
{
auto it = mp.begin();
printf("%lld\n", it->second);
mp.erase(it);
}
else
{
auto it = --mp.end();
printf("%lld\n", it->second);
mp.erase(it);
}
}
return 0;
} 问题 Q: 第K小乘积
题目描述
给定一个长度为 n 的序列 {a1,a2,...,an} 。
如果我们任选两个数 x,y (1≤x
将所有的 ax⋅ay 放入一个新序列,得到{b1,b2,...,![]() } ,并将其由小到大排序。
} ,并将其由小到大排序。
请你求出 bk 的值。
输入
输入第一行,两个整数 n,k 。 (2≤n≤2×105,1≤k≤![]() )
)
输入第二行,n 个整数 ai。(−109≤ai≤109)
输出
请输出一个整数,即题意中 bk 的值。
样例输入 复制
4 3
3 3 -4 -2样例输出 复制
-6提示
样例解释:排序后, b={−12,−12,−6,−6,8,9}.
则 b3=-6
代码://这道题我也没写对。。但感觉应该是分治
#include
using namespace std;
typedef long long ll;
ll partition(ll a[], ll l, ll r) {
ll low = l, high = r;
ll temp = a[l];
while (low < high) {
while (low < high && a[high] >= temp)
high--;
a[low] = a[high];
while (low < high && a[low] <= temp)
low++;
a[high] = a[low];
}
a[low] = temp;
return low;
}
int findk(ll a[], ll l, ll r, ll k) {
ll temp = partition(a, l, r);
if (temp - l + 1 == k)
return a[temp];
else if (temp - l + 1 < k)
return findk(a, temp + 1, r, k - temp + l - 1);
else
return findk(a, l, temp - 1, k);
}
int main() {
ll n, k, top = 0;
cin >> n >> k;
ll a[n + 5], b[n * (n - 1) / 2 + 5];
for (ll i = 0; i < n; i++)
cin >> a[i];
for (ll i = 0; i < n; i++) {
for (ll j = 0; j < i; j++) {
b[top++] = a[i] * a[j];
}
}
cout << findk(b, 0, top - 1, k);
return 0;
} 问题 R: 消灭大整数
题目描述
有一个巨大的整数 x ,现在的任务是消灭它,目标是把它变成 0 。
在每一次操作中,你可以选择任意一个自然数 k ,然后你选择其中一项:
① 令 x=x+10^k
② 令 x=x−10^k
请问,你最少需要几次操作才能消灭掉这个整数 x ?
输入
输入一个整数,x (1≤x≤10^1000000)
使用者请将您代码中的换成,因为输入时会添加多余的空格,可能会使得您答案有误。*Python 使用者请将您代码中的 input()换成 input().strip() ,因为BUCTOJ输入时会添加多余的空格,可能会使得您答案有误。
输出
请输出一个整数,代表最少的操作次数。
样例输入 复制
91样例输出 复制
3提示
样例一解释:
操作一: 令k=0 , 则 91−100=90
操作一: 令k=1 , 则 90+101=100
操作一: 令k=2 , 则 100−102=0
样例输入2
314159265358979323846264338327950288419716939937551058209749445923078164062862089986280348253421170
样例输出2
243
AC代码:
#include
using namespace std;
int main()
{
int sum = 0;
string s;
cin >> s;
int i;
for (i = s.size() - 1; i > 0; i--)
{
if (s[i] == '0')
;
else if (s[i] < '5')
sum += (s[i] - '0');
else if (s[i] == '5')
{
if (s[i - 1] < '5')
{
sum += (s[i] - '0');
}
else
{ // 进位
sum += (10 - s[i] + '0');
if (s[i - 1] != '9')
s[i - 1]++;
else
{ // 799997
i--;
while (i >= 0 && s[i] == '9')
{
i--;
}
if (i < 0)
sum++;
else
{
s[i]++;
i++;
}
}
}
}
else if (s[i] < '9')
{
sum += (10 - s[i] + '0');
if (s[i - 1] != '9')
s[i - 1]++;
else
{ // 799997
i--;
while (i >= 0 && s[i] == '9')
{
i--;
}
if (i < 0)
sum++;
else
{
s[i]++;
i++;
}
}
}
else if (s[i] == '9')
{
if (s[i - 1] != '9')
{
s[i - 1]++;
sum++;
}
else
{
sum++;
while (s[i] == '9' && i >= 0)
{
i--;
}
if (i < 0)
sum++;
else
{
s[i]++;
i++;
}
}
}
}
if (s[0] <= '5')
sum += (s[0] - '0');
else if (s[0] != '9' && s[0] > '5')
sum += (11 - s[0] + '0');
else if (i >= 0)
sum += 2;
cout << sum;
return 0;
} 问题 S: 关灯
题目描述
公路上有 n 盏路灯,若把公路视为一个数轴,那么第 i 盏路灯的坐标在 ai ,它的开关状态是 bi。
同时,有 m 个按钮,第 j 个按钮可以将坐标位于区间 [Lj,Rj] 内的所有路灯开关状态反转。
由于电力不稳,现在限制每个按钮最多只能按一次。
请问能否将所有路灯都关闭?如果可以,请输出一组关闭方案中需要按下按钮的编号。
输入
输入第一行,两个整数 n,m (1≤n≤105,1≤m≤2×105)
接下来 n 行,每行两个整数 ai,bi (1≤ai≤109,0≤bi≤1)
保证 ai 互不相同。 bi=0 代表路灯关闭,bi=1 代表路灯开启。
接下来 m 行,每行两个整数 Lj,Rj (1≤Lj≤Rj≤109)
输出
如果不能将所有路灯关闭,请输出 -1
如果可以将所有路灯关闭,请输出两行:
输出第一行,一个整数 M ,代表需要按下的按钮数。
输出第二行,M 个整数,代表需要按下的按钮编号 (顺序任意)。
样例输入 复制
3 4
5 1
10 1
8 0
1 10
4 5
6 7
8 9样例输出 复制
2
1 4提示
样例输入2
4 2 2 0 3 1 5 1 7 0 1 4 4 7
样例输出2
-1
样例输入3
3 2 5 0 10 0 8 0 6 9 66 99
样例输出3
0
AC代码://不会
502 Not Found问题 T: 计信狗的大一下
题目描述
学了一年计算机就会搞花活,有一天他又想起了一个有趣的问题:
给定一个数组 d,长度为 k,有q 个询问
每个询问会给出三个整数,n,x,m,接着按照下列公式,生成一个长度为 n 的数组 a
问在 a 中,有多少个下标 i 满足 a[i] mod m
*提示,A mod B 为取模运算
输入
第一行输入 ,1≤k,q≤5000
接下来输入数组 d (0≤d[i]≤109)
然后 q 行,每行有三个整数,代表 n,x,m(2≤n,m≤109,0≤x≤109)
输出
输出共 q 行,对于每个询问,输出一个整数
样例输入 复制
3 1
3 1 4
5 3 2
样例输出 复制
1AC代码://不会
502 Not Found