数据结构(二)------单链表
制作不易,三连支持一下呗!!!
文章目录
- 前言
- 一.什么是链表
- 二.链表的分类
- 三.单链表的实现
- 总结
前言
上一节,我们介绍了顺序表的实现与一些经典算法。
但是顺序表这个数据结构依然有不少缺陷:
1.顺序表指定位置和头部的插入和删除操作的时间复杂度为o(n)。
2.增容需要重新申请新的空间,拷贝旧数据,释放旧空间有不小的损耗。
3.增容是成倍数的扩容,难免还会存在一定的空间浪费。
问题来了:有没有一种数据结构是可以弥补上述顺序表中存在的一些缺点的。答案是肯定的——链表
一.什么是链表
链表的结构就像火车的一节一节的车厢,每节车厢单独用来容纳乘客,但是彼此之间又用链条相互勾连在一起。同时从第一节车厢想要到达第三节车厢必须要经过第二节车厢。
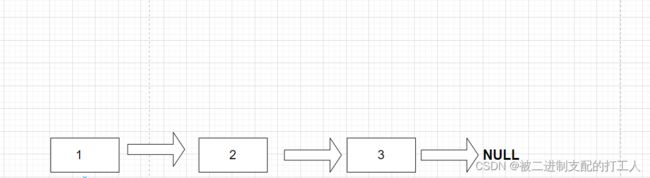
链表依然属于线性表,它在逻辑结构上是连续的,但是物理结构上是不连续的!
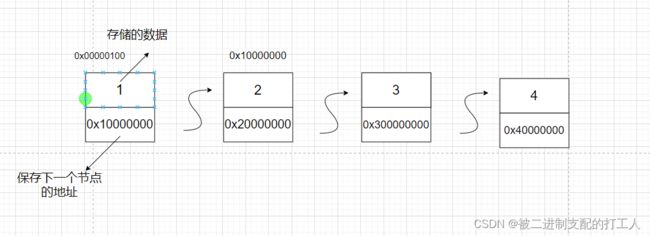
链表在逻辑结构上大概是这样的:
而这里的每一节“车厢“,我们称之为”节点(结点)“ 。每个节点又是由两个部分组成:一部分用来存储数据,另一部分则是保存下一个节点的地址,以便我们找到下一个节点。链表就是这样通过指针将物理结构上不连续的数据串联在了一起。
二.链表的分类:
链表的分类依据有三点:
1.带头与不带头
2.循环与不循环
3.单向与双向
通过这三种依据的排列组合,链表共可以分为2*2*2=8种。(我们主要学习单链表(不带头单向不循环链表)与双向链表(带头双向不循环链表,下一节介绍))。
下面我们解释一下这三种依据是什么意思:
1.带头与不带头
带头是指带有头节点的链表,所谓头节点是指第一个节点(但是这个节点不保存有效数据,只记录下一个节点的地址,是一个无效的节点),就像放哨的一样,所以也叫“哨兵卫”。
逻辑结构如下:
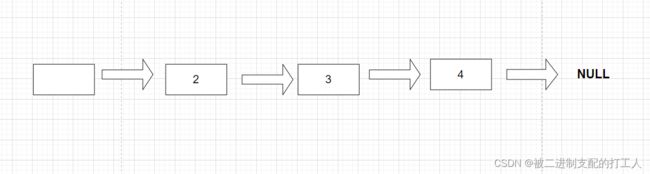
不带头就是指从第一个节点开始就存储有有效的数据的链表
2.循环与不循环
不循环链表的结尾一定是NULL,以表示链表已结束。
逻辑结构就是这样:
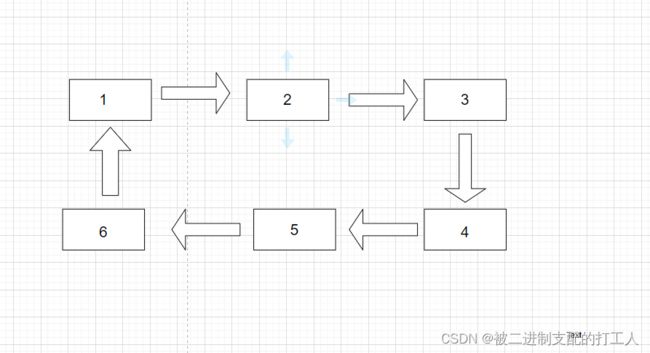
而循环链表 则是将不循环链表首尾相连,让它们形成封闭的图形。
逻辑结构如下:
3.单向与双向
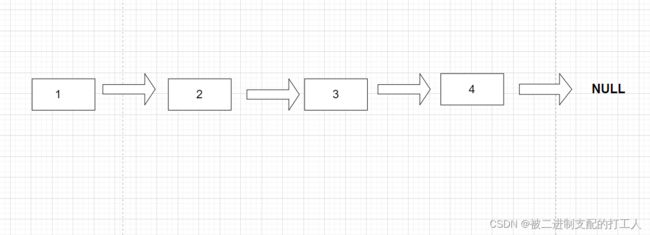
单向链表就是指通过前驱节点可以找到后继节点,但是无法通过后继节点找到前驱节点
逻辑结构如下:
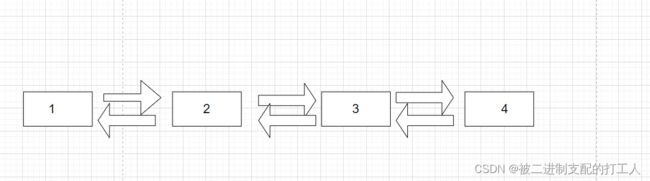
双向链表则是既可以通过前驱节点找到后继节点,也能通过后继节点找回前驱节点
逻辑结构如下:
三.单链表的实现
我们这一节则是来介绍单链表的实现过程,完成对单链表进行增,删,查,改的接口。
1.单链表节点的定义
根据前面对单链表的介绍,我们知道单链表由两部分组成,一个是保存数据,另一个是保存下一个节点的地址,所以我们可以自然的写出这种结构。
typedef int SLDataType;//重定义方便我们后续存储数据类型发生改变时,一键替换
typedef struct SListNode
{
SLDataType data;
struct SListNode *next;
}SLTNode; //重定义方便我们后续书写
2.单链表的打印
我们接下来先写一个打印单链表的接口,以方便我们后续调试代码!
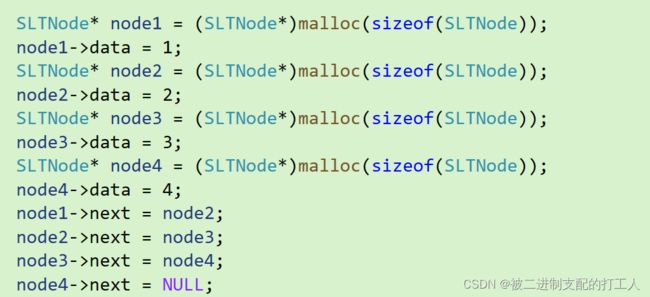
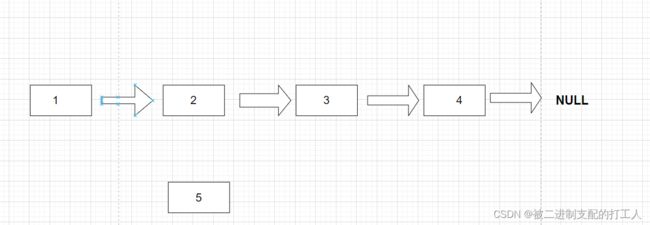
由于我们还没有申请节点的接口,所以我们首先先手动申请4个节点,并把它们链在一起。
画图的话就是这个样子。
如果我们想打印这串链表,通过分析可知,我们可以通过循环遍历这个链表,判断条件是当前节点是否为NULL。每次打印结束将下个节点作为新的节点来打印。
代码实现如下:
void SListPrint(SLTNode* node1)
{
SLTNode* ps = node1;//直接用node1会导致后面找不到头节点
while (ps)
{
printf("%d->", ps->data);
ps = ps->next;
}
printf("NULL\n");
}
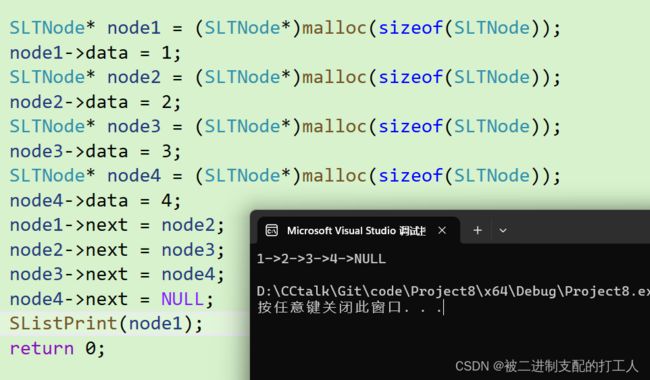
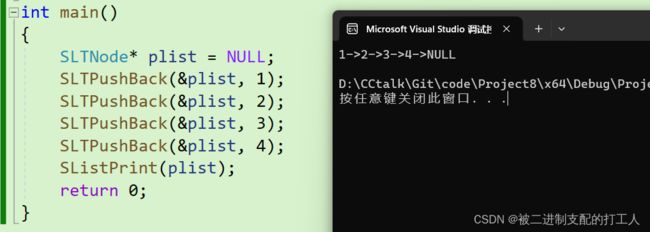
在VS2022上对上述代码的运行结果如下:
打印结果与我们预期结果相符,没有问题。
3.创建新节点
我们后续插入数据时都会创建新的节点,所以我们将这个功能单独拿出来实现一个创建新节点的接口。
SLTNode* SLTBuyNode(SLDataType x)//x是要插入的数据
{
SLTNode* nownode = (SLTNode*)malloc(sizeof(SLTNode));
if (newnode == NULL)
{
perror("malloc");
exit(1);
}
nownode->data = x;
nownode->next = NULL;
return nownode;
}
4.尾插和头插
<1>.尾插
当链表不为空时:
假设我们现在要在当前链表后尾插一个节点5。思路就是先创建一个新节点5,通过循环找到当前的尾节点4,将node4->next改为node5。
当链表为空时:
直接将新节点作为头节点即可。
代码实现如下:
void SLTPushBack(SLTNode** pphead, SLDataType x)//注意:这里一定要传址调用,否则链表为空的情况就无法插入成功
{
assert(pphead);//pphead不能为空,因为我们在函数中需要对pphead解引用
SLTNode* newnode = SLTBuyNode(x);
if (*pphead == NULL)//链表为空,将新节点直接作为头节点
{
*pphead = newnode;
return;
}
SLTNode* ptail = *pphead;
while (ptail->next)
{
ptail = ptail->next;
}
//循环结束后,ptail就是尾节点
ptail->next = newnode;
}测试样例:
注意: 如果这里我们直接将头节点的地址传进来,而不是传入指向头节点的指针的地址,那么当头节点为空时,形参pphead是头节点地址的临时拷贝,将pphead赋值为nownode并不会改变实参plist,就会导致永远无法插入第一个节点。
<2>.头插
还是要将5插入到链表中,思路就是先创建一个新节点newnode,让newnode->next=*pphead,并将头节点*pphead赋值为newnode(也就是新的头节点)。
代码实现如下:
void SLTPushFront(SLTNode**pphead, SLDataType x)
{
assert(pphead); //pphead不能为空,因为我们在函数中需要对pphead解引用
SLTNode* newnode= SLTBuyNode(x);
newnode->next = *pphead;
*pphead = newnode;
}测试样例:
5.头删和尾删
<1>.头删
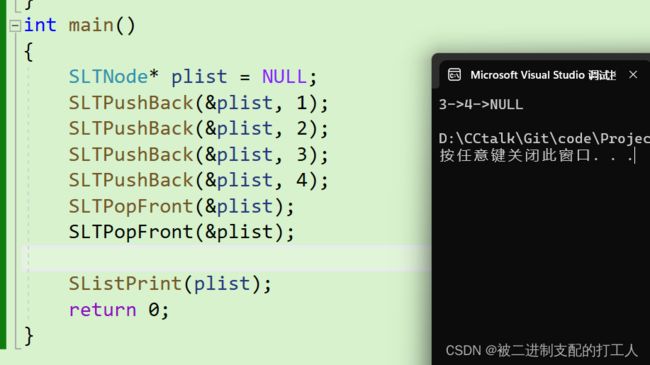
假设我们要头删掉1这个节点,整体思路就是重新创建一个变量用来保存头节点的后继节点(因为我们接下来要释放掉头节点,不保存一份会导致找不到第二个节点),然后释放掉原来的头节点,并将其置为NULL。 然后将头节点赋值为原来的第二个节点。
代码实现如下:
void SLTPopFront(SLTNode** pphead)
{
assert(pphead);
assert(*pphead);//链表不能为空
//让第二个节点成为新的头节点,并释放掉旧的头节点
SLTNode* next = (*pphead)->next;
free(*pphead);
*pphead = next;
}测试样例如下:
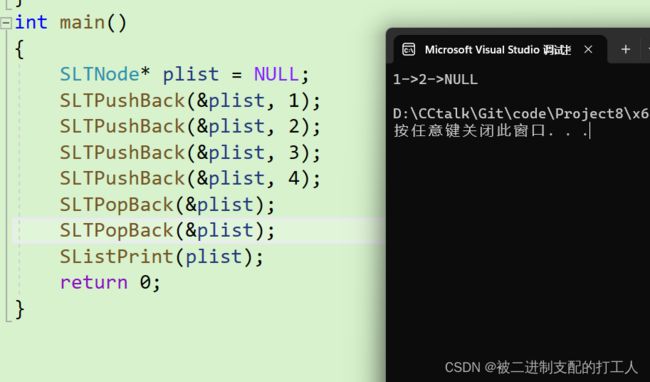
<2>.尾删
假设我们想要尾删掉4这个节点,我们都思路就是通过while循环找到尾节点和尾节点的前驱节点。将尾节点的前驱节点置为NULL,释放掉尾节点,并将指向尾节点的指针置为空。
注意:这样有一个特殊的情况就是当链表中只有一个节点时,头节点也就同时是尾节点,这样是没有尾节点的前驱节点的。所以这种情况需要单独考虑!!!
代码实现如下:
void SLTPopBack(SLTNode** pphead, SLDataType x)
{
assert(pphead);
assert(*pphead);//链表不能为空
SLTNode* prev = NULL;
SLTNode* pcur = *pphead;
if (pcur->next == NULL)//只有一个节点的情况
{
free(*pphead);
*pphead = NULL;
return;
}
while (pcur->next)
{
prev = pcur;
pcur = pcur->next;
}
prev->next = NULL;
//销毁尾节点
free(pcur);
pcur = NULL;
}
样例测试如下:
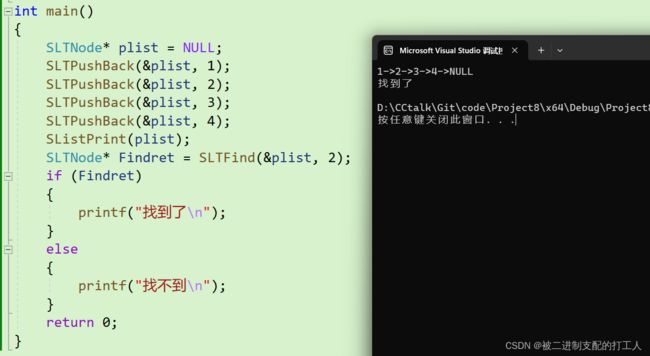
6.查找
思路很简单:遍历链表,遇到要找的值就返回这个节点的地址,找不到返回NULL。
代码实现如下:
SLTNode* SLTFind(SLTNode** pphead, SLDataType x)//查找数据x,并返回节点的地址
{
assert(pphead);
SLTNode* pcur = *pphead;
//遍历链表
while (pcur)
{
if (pcur->data == x)
{
return pcur;
}
pcur = pcur->next;
}
//找不到返回NULL
return NULL;
}
测试样例 :
7.指定位置的插入和删除
<1>.指定位置之前插入数据
思路:找到目标节点和目标节点的前驱节点,改变目标节点的前驱节点的方向,将新节点串联进来。
pos可以通过查找接口来获取!!!
代码实现如下:
void SLTInsertFront(SLTNode** pphead, SLTNode* pos, SLDataType x)
{
assert(pphead);
assert(pos);//指定位置肯定不能为空
assert(*pphead);//如果链表为空,指定位置一定为空,所以链表不能为空
SLTNode* newnode = SLTBuyNode(x);
SLTNode* prev = *pphead;
if (pos == *pphead)//特殊情况,特殊处理
{
SLTPushFront(pphead, x);
return;
}
while (prev->next != pos)
{
prev = prev->next;
}
prev->next = newnode;
newnode->next = pos;
}这里要注意一种特殊的情况:pos是头节点时,while循环将永远无法找到pos。这里我们直接调用之前实现的头插接口即可! ! !
<2>.指定位置之后插入数据
思路就是:先创建新节点newnode,再将newnode的后继节点赋为指定位置pos的后继节点,再将指定位置pos的后继节点置为newnode。
代码实现如下:
void SLTInsertAfter(SLTNode* pos, SLDataType x)
{
assert(pos);
SLTNode* newnode = SLTBuyNode(x);
newnode->next = pos->next;
pos->next = newnode;
}注意: 我们不需要传入头节点,因为只要有pos就可以找到pos之后的所有节点!!!
<3>.删除指定位置的节点
代码实现如下:
void SLTErase(SLTNode** pphead, SLTNode* pos)
{
assert(pphead);
assert(*pphead);//链表为空就无法删除,不能为空
assert(pos);
SLTNode* prev = *pphead;//
if (pos == *pphead)//如果pos为头节点,没有前驱节点
{
//头删
SLTPopFront(pphead);
return;
}
while (prev->next != pos)
{
prev = prev->next;
}
prev->next = pos->next;
free(pos);
pos = NULL;
}
<4>.指定位置之后删除数据
思路和指定位置之后插入数据类似,也是先找到pos和pos->next,再改变链表方向,最后释放pos->next节点。
代码实现如下:
void SLTEraseAfter(SLTNode* pos)
{
assert(pos);
assert(pos->next);
SLTNode* del = pos->next;
pos->next = pos->next->next;
free(del);
del = NULL;
}
8.销毁链表
void SLTDesTroy(SLTNode** pphead)
{
assert(pphead);
assert(*pphead);
SLTNode* pcur = *pphead;
while (pcur)
{
SLTNode* next = pcur->next;
free(pcur);
pcur = next;
}
*pphead = NULL;
}总结
单链表的所有代码放在这里,以供参考!!!
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
typedef int SLDataType;//重定义方便我们后续存储数据类型发生改变时,一键替换
typedef struct SListNode
{
SLDataType data;
struct SListNode *next;
}SLTNode; //重定义方便我们后续书写
void SListPrint(SLTNode* node1)
{
SLTNode* ps = node1;
while (ps)
{
printf("%d->", ps->data);
ps = ps->next;
}
printf("NULL\n");
}
SLTNode* SLTBuyNode(SLDataType x)//x是要插入的数据
{
SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
if (newnode == NULL)
{
perror("malloc");
exit(1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
void SLTPushBack(SLTNode** pphead, SLDataType x)//注意:这里一定要传址调用,否则链表为空的情况就无法插入成功
{
assert(pphead);//pphead不能为空,因为我们在函数中需要对pphead解引用
SLTNode* newnode = SLTBuyNode(x);
if (*pphead == NULL)//链表为空,将新节点直接作为头节点
{
*pphead = newnode;
return;
}
SLTNode* ptail = *pphead;
while (ptail->next)
{
ptail = ptail->next;
}
//循环结束后,ptail就是尾节点
ptail->next = newnode;
}
void SLTPushFront(SLTNode**pphead, SLDataType x)
{
assert(pphead); //pphead不能为空,因为我们在函数中需要对pphead解引用
SLTNode* newnode= SLTBuyNode(x);
newnode->next = *pphead;
*pphead = newnode;
}
void SLTPopBack(SLTNode** pphead)
{
assert(pphead);
assert(*pphead);//链表不能为空
SLTNode* prev = NULL;
SLTNode* pcur = *pphead;
if (pcur->next == NULL)//只有一个节点的情况
{
free(*pphead);
*pphead = NULL;
return;
}
while (pcur->next)
{
prev = pcur;
pcur = pcur->next;
}
prev->next = NULL;
//销毁尾节点
free(pcur);
pcur = NULL;
}
void SLTPopFront(SLTNode** pphead)
{
assert(pphead);
assert(*pphead);//链表不能为空
//让第二个节点成为新的头节点,并释放掉旧的头节点
SLTNode* next = (*pphead)->next;
free(*pphead);
*pphead = next;
}
SLTNode* SLTFind(SLTNode** pphead, SLDataType x)//查找数据x,并返回节点的地址
{
assert(pphead);
SLTNode* pcur = *pphead;
//遍历链表
while (pcur)
{
if (pcur->data == x)
{
return pcur;
}
pcur = pcur->next;
}
//找不到返回NULL
return NULL;
}
void SLTInsertFront(SLTNode** pphead, SLTNode* pos, SLDataType x)
{
assert(pphead);
assert(pos);//指定位置肯定不能为空
assert(*pphead);//如果链表为空,指定位置一定为空,所以链表不能为空
SLTNode* newnode = SLTBuyNode(x);
SLTNode* prev = *pphead;
if (pos == *pphead)//特殊情况,特殊处理
{
SLTPushFront(pphead, x);
return;
}
while (prev->next != pos)
{
prev = prev->next;
}
prev->next = newnode;
newnode->next = pos;
}
void SLTInsertAfter(SLTNode* pos, SLDataType x)
{
assert(pos);
SLTNode* newnode = SLTBuyNode(x);
newnode->next = pos->next;
pos->next = newnode;
}
void SLTErase(SLTNode** pphead, SLTNode* pos)
{
assert(pphead);
assert(*pphead);//链表为空就无法删除,不能为空
assert(pos);
SLTNode* prev = *pphead;//
if (pos == *pphead)//如果pos为头节点,没有前驱节点
{
//头删
SLTPopFront(pphead);
return;
}
while (prev->next != pos)
{
prev = prev->next;
}
prev->next = pos->next;
free(pos);
pos = NULL;
}
void SLTEraseAfter(SLTNode* pos)
{
assert(pos);
assert(pos->next);
SLTNode* del = pos->next;
pos->next = pos->next->next;
free(del);
del = NULL;
}
void SLTDesTroy(SLTNode** pphead)
{
assert(pphead);
assert(*pphead);
SLTNode* pcur = *pphead;
while (pcur)
{
SLTNode* next = pcur->next;
free(pcur);
pcur = next;
}
*pphead = NULL;
}
int main()
{
SLTNode* plist = NULL;
SLTPushBack(&plist, 1);
SLTPushBack(&plist, 2);
SLTPushBack(&plist, 3);
SLTPushBack(&plist, 4);
SListPrint(plist);
SLTNode* Findret = SLTFind(&plist, 2);
if (Findret)
{
printf("找到了\n");
}
else
{
printf("找不到\n");
}
return 0;
}