C语言初阶之操作符
一、操作符分类
- 算术操作符 + - * / %
- 移位操作符 << >>
- 位操作符 & | ^
- 赋值操作符 = += -= *= /=
- 单目操作符 ! sizeof + - ~ & *
- 关系操作符 > < >= <= == !=
- 逻辑操作符 && ||
- 条件操作符 ? :
- 逗号表达式 ,
- 下标引用、函数调用和结构成员 [] () . ->
二、算数操作符
+ - * / %- / 除法
- 整数除法(除号两端都是整数)
- 浮点数除法(除号两端只要有一个小数就执行小数除法)
- % 取模操作符的两个操作数必须是整数
- 除了 % 操作符之外,其他的几个操作符可以作用于整数和浮点数。
- 对于 / 操作符如果两个操作数都为整数,执行整数除法。而只要有浮点数执行的就是浮点数除法。
三、移位操作符
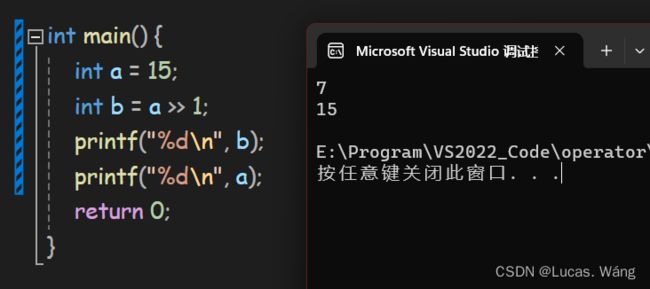
<< 左移操作符
>> 右移操作符
注:移位操作符的操作数只能是整数。移动的是补码二进制
1)左移
左边抛弃、右边补0
2)右移
- 逻辑移位 左边用0填充,右边丢弃
- 算术移位 左边用原该值的符号位填充,右边丢弃
一般编译器采用算数右移
a移位赋值给b,但a本身不变。
四、位操作符
位操作符有:
& //按位与
| //按位或
^ //按位异或
//注:他们的操作数必须是整数。& //按位与 - 只有两个数的二进制同时为1,结果才为1,否则为0。(负数按补码形式参加按位与运算)
| //按位或 - 参加运算的两个数只要两个数中的一个为1,结果就为1。
^ //按位异或 - 对应二进制位相同为0,相异为1
//方法2:
#include
int main()
{
int num = -1;
int i = 0;
int count = 0;//计数
for (i = 0; i < 32; i++)
{
if (num & (1 << i))
count++;
}
printf("二进制中1的个数 = %d\n", count);
return 0;
}
//思考还能不能更加优化,这里必须循环32次的。
//方法3:
#include
int main()
{
int num = -1;
int i = 0;
int count = 0;//计数
while (num)
{
count++;
num = num & (num - 1);
}
printf("二进制中1的个数 = %d\n", count);
return 0;
}
//这种方式是不是很好?达到了优化的效果,但是难以想到 当 num 的值为 -1 时,程序会计算 -1 的二进制表示中包含的1的个数。
-1 的二进制表示为 1111 1111(根据补码表示法),其中共有8个1。程序会使用 Brian Kernighan's 算法来计算这个值。
首先,初始化 count 为 0。
进入循环,第一次迭代:
num的值为 -1,二进制表示为 1111 1111。- 执行
num = num & (num - 1),即-1 = -1 & (-1 - 1),得到-1 = -1 & -2。 -2的二进制表示为 1111 1110。num的新值为-2。count的值增加1,变为 1。
进入下一次迭代:
num的值为-2,二进制表示为 1111 1110。- 执行
num = num & (num - 1),即-2 = -2 & (-2 - 1),得到-2 = -2 & -3。 -3的二进制表示为 1111 1101。num的新值为-3。count的值增加1,变为 2。
继续迭代,每次迭代都会消除一个1,直到 num 变为0。
五、赋值操作符
赋值操作符可以连续使用,比如:
int a = 10;
int x = 0;
int y = 20;
a = x = y + 1;//连续赋值
//x = y+1;
//a = x;复合赋值符
+=
-=
*=
/=
%=
>>=
<<=
&=
|=
^=
六、单目操作符
1)单目操作符介绍
! 逻辑反操作
- 负值
+ 正值
& 取地址
sizeof 操作数的类型长度(以字节为单位)
~ 对一个数的二进制按位取反
-- 前置、后置--
++ 前置、后置++
* 间接访问操作符(解引用操作符)
(类型) 强制类型转换2)取地址与解引用
int main() {
int a = 10;
//pa是指针变量
int* pa = &a;
*pa = 20; //解引操作符(间接访问操作符)- 通用pa中存放的地址,找到指向的空间(内容)
int c = *pa;
return 0;
}3)sizeof和数组
sizeof不是函数,是操作符,计算的是类型创建变量的大小,单位是字节。
#include
void test1(int arr[])
{
printf("%d\n", sizeof(arr));//(2)
}
void test2(char ch[])
{
printf("%d\n", sizeof(ch));//(4)
}
int main()
{
int arr[10] = { 0 };
char ch[10] = { 0 };
printf("%d\n", sizeof(arr));//(1)
printf("%d\n", sizeof(ch));//(3)
test1(arr);
test2(ch);
return 0;
} 传递数组名实质是传递数组首地址。
七、关系操作符
>
>=
<
<=
!= 用于测试“不相等”
== 用于测试“相等”对比整型浮点型,不能比较字符串
八、逻辑操作符
&& 逻辑与
|| 逻辑或
区分逻辑与和按位与 区分逻辑或和按位或,如果结果是真用1表示,是假用0表示。
1&2----->0
1&&2---->1
1|2----->3
1||2---->1
a++为后置++,a运算时为0,为假,不继续进行后面的&&运算。
或者运算 || 左边为真,不进行后面的运算。
九、条件操作符
exp1 ? exp2 : exp3 //三目操作符
真 执行 不执行
假 不执行 执行十、逗号表达式
exp1, exp2, exp3, …expN- 逗号表达式,就是用逗号隔开的多个表达式。
- 逗号表达式,从左向右依次执行。整个表达式的结果是最后一个表达式的结果。
//代码1
int a = 1;
int b = 2;
int c = (a>b, a=b+10, a, b=a+1);//逗号表达式
c是多少? c=13
十一、下标引用、函数调用和结构成员
1)[ ] 下标引用操作符
操作数:一个数组名 + 一个索引值
int arr[10];//创建数组
arr[9] = 10;//实用下标引用操作符。
[ ]的两个操作数是arr和9。2)( ) 函数调用操作符
接受一个或者多个操作数:第一个操作数是函数名,剩余的操作数就是传递给函数的参数。
#include
void test1()
{
printf("hehe\n");
}
void test2(const char* str)
{
printf("%s\n", str);
}
int main()
{
test1(); //实用()作为函数调用操作符。
test2("hello bit.");//实用()作为函数调用操作符。
return 0;
} 3)访问一个结构的成员
- . 结构体.成员名
- -> 结构体指针->成员名
#include
struct Stu{
char name[10];
int age;
char sex[5];
double score;
};
void set_age1(struct Stu stu){
stu.age = 18;
}
void set_age2(struct Stu* pStu){
pStu->age = 18;//结构成员访问
}
void Print(struct Stu* p) {
printf("%s %d %s %lf", (*p).name, (*p).age, (*p).sex, (*p).score);
printf("%s %d %s %lf", p->name, p->age, p->sex, p->score);//结构体指针->成员名
}
int main(){
struct Stu stu;
struct Stu* pStu = &stu;//结构成员访问
stu.age = 20;//结构成员访问
set_age1(stu);
pStu->age = 20;//结构成员访问
set_age2(pStu);
printf("%s %d %s %lf", stu.name, stu.age, stu.sex, stu.score);
return 0;
} 十二、表达式求值
- 表达式求值的顺序一部分是由操作符的优先级和结合性决定。
- 同样,有些表达式的操作数在求值的过程中可能需要转换为其他类型。
1)隐式类型转换
C的整型算术运算总是至少以缺省整型类型的精度来进行的。
为了获得这个精度,表达式中的字符(char)和短整型(short)操作数在使用之前被转换为普通整型,这种转换称为整型提升。
- 表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度 一般就是int的字节长度,同时也是CPU的通用寄存器的长度。
- 因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
- 通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令 中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int,然后才能送入CPU去执行运算。
int main() {
char c1 = 5;
//00000000000000000000000000000101,存不下,截断
//00000101 - c1
char c2 = 127;
//00000000000000000000000001111111,存不下,截断
//01111111 - c2
char c3 = c1 + c2;
//补回,整型提升
//00000000000000000000000000000101
//00000000000000000000000001111111
//00000000000000000000000010000100,存不下,截断
//10000100 - c3
//%d,十进制形式打印有符号的整数
//11111111111111111111111110000100 - 提升,高位补1 - 补码
//100000000000000000000000011111100 --> -124
printf("%d\n", c3);
return 0;
}整形提升是按照变量的数据类型的符号位来提升的。
//负数的整形提升
char c1 = -1;
变量c1的二进制位(补码)中只有8个比特位:
1111111
因为 char 为有符号的 char
所以整形提升的时候,高位补充符号位,即为1
提升之后的结果是:
11111111111111111111111111111111
//正数的整形提升
char c2 = 1;
变量c2的二进制位(补码)中只有8个比特位:
00000001
因为 char 为有符号的 char
所以整形提升的时候,高位补充符号位,即为0
提升之后的结果是:
00000000000000000000000000000001
//无符号整形提升,高位补0实例1中的a,b要进行整形提升,但是c不需要整形提升
//实例1
int main()
{
char a = 0xb6;
short b = 0xb600;
int c = 0xb6000000;
if (a == 0xb6)
printf("a");
if (b == 0xb600)
printf("b");
if (c == 0xb6000000)
printf("c");
return 0;
}a,b整形提升之后,变成了负数,所以表达式 a==0xb6 , b==0xb600 的结果是假,但是c不发生整形提升,则表 达式 c==0xb6000000 的结果是真.
//实例2
int main()
{
char c = 1;
printf("%u\n", sizeof(c));
printf("%u\n", sizeof(+c));
printf("%u\n", sizeof(-c));
return 0;
}实例2中的,c只要参与表达式运算,就会发生整形提升,表达式 +c ,就会发生提升,所以 sizeof(+c) 是4个字节。
表达式 -c 也会发生整形提升,所以 sizeof(-c) 是4个字节,但是 sizeof(c) ,就是1个字节。
2)算术转换
如果某个操作符的各个操作数属于不同的类型,那么除非其中一个操作数的转换为另一个操作数的类 型,否则操作就无法进行。下面的层次体系称为寻常算术转换。
long double
double
float
unsigned long int
long int
unsigned int
int
如果某个操作数的类型在上面这个列表中排名较低,那么首先要转换为另外一个操作数的类型后执行运 算。
但是算术转换要合理,要不然会有一些潜在的问题。
float f = 3.14;
int num = f;//隐式转换,会有精度丢失
3)操作符属性
复杂表达式的求值有三个影响的因素。
- 操作符的优先级
- 操作符的结合性
- 是否控制求值顺序
两个相邻的操作符先执行哪个?取决于他们的优先级。如果两者的优先级相同,取决于他们的结合性。
操作符优先级
| 操作符 | 描述 | 用法示例 | 结果类型 | 结合性 | 是否控制求值顺序 |
| () | 聚组 | (表达式) | 与表达式同 | N/A | 否 |
| () | 函数调用 | rexp(rexp,...,rexp) | rexp | L-R | 否 |
| [ ] | 下标引用 | rexp[rexp] | lexp | L-R | 否 |
| . | 访问结构成员 | lexp.member_name | lexp | L-R | 否 |
| -> | 访问结构指针成员 | rexp->member_name | lexp | L-R | 否 |
| ++ | 后缀自增 | lexp++ | rexp | L-R | 否 |
| -- | 后缀自减 | lexp-- | rexp | L-R | 否 |
| ! | 逻辑反 | !rexp | rexp | R-L | 否 |
| ~ | 按位取反 | ~rexp | rexp | R-L | 否 |
| + | 单目,表示正值 | +rexp | rexp | R-L | 否 |
| - | 单目,表示负值 | -rexp | rexp | R-L | 否 |
| ++ | 前缀自增 | ++rexp | rexp | R-L | 否 |
| -- | 前缀自减 | --rexp | rexp | R-L | 否 |
| * | 间接访问 | *rexp | lexp | R-L | 否 |
| & | 取地址 | &rexp | rexp | R-L | 否 |
| sizeof | 取其长度,以字节表示 | sizeof rexp sizeof(类型) | rexp | R-L | 否 |
| (类型) | 类型转换 | (类型) rexp | rexp | R-L | 否 |
| * | 乘法 | rexp * rexp | rexp | L-R | 否 |
| / | 除法 | rexp / rexp | rexp | L-R | 否 |
| % | 整数取余 | rexp % rexp | rexp | L-R | 否 |
| + | 加法 | rexp + rexp | rexp | L-R | 否 |
| - | 减法 | rexp - rexp | rexp | L-R | 否 |
| << | 左移位 | rexp << rexp | rexp | L-R | 否 |
| >> | 右移位 | rexp >> rexp | rexp | L-R | 否 |
| > | 大于 | rexp > rexp | rexp | L-R | 否 |
| >= | 大于等于 | rexp >= rexp | rexp | L-R | 否 |
| < | 小于 | rexp < rexp | rexp | L-R | 否 |
| <= | 小于等于 | rexp <= rexp | rexp | L-R | 否 |
| == | 等于 | rexp == rexp | rexp | L-R | 否 |
| != | 不等于 | rexp != rexp | rexp | L-R | 否 |
| & | 位与 | rexp & rexp | rexp | L-R | 否 |
| ^ | 位异或 | rexp ^ rexp | rexp | L-R | 否 |
| | | 位或 | rexp | rexp | rexp | L-R | 否 |
| && | 逻辑与 | rexp && rexp | rexp | L-R | 是 |
| || | 逻辑或 | rexp || rexp | rexp | L-R | 是 |
| ? : | 条件操作符 | rexp ? rexp : rexp | rexp | N/A | 是 |
| = | 赋值 | lexp = rexp | rexp | R-L | 否 |
| += | 以...加 | lexp += rexp | rexp | R-L | 否 |
| -= | 以...减 | lexp -= rexp | rexp | R-L | 否 |
| *= | 以...乘 | lexp *= rexp | rexp | R-L | 否 |
| /= | 以...除 | lexp /= rexp | rexp | R-L | 否 |
| %= | 以...取模 | lexp %= rexp | rexp | R-L | 否 |
| <<= | 以...左移 | lexp <<= rexp | rexp | R-L | 否 |
| >>= | 以...右移 | lexp >>= rexp | rexp | R-L | 否 |
| &= | 以...与 | lexp &= rexp | rexp | R-L | 否 |
| ^= | 以...异或 | lexp ^= rexp | rexp | R-L | 否 |
| |= | 以...或 | lexp |= rexp | rexp | R-L | 否 |
| , | 逗号 | rexp | rexp | L-R | 是 |
总结:
我们写出的表达式如果不能通过操作符的属性确定唯一的计算路径,那这个表达式就是存在问题的。