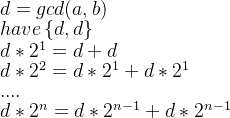寒假思维训练day15 牛客练习赛121

牛客练习赛ABCD题解，更新一个题解作为今天的任务收尾。

---

寒假思维训练day15

摘要：

Part1：B题，B-You Brought Me A Gentle Breeze on the Field_牛客练习赛121 (nowcoder.com)

Part2:  C题，C-氧气少年的水滴 2_牛客练习赛121 (nowcoder.com)

part3:  D题，D-氧气少年的 LCM_牛客练习赛121 (nowcoder.com)

---

Part1  B题:

1、题意：

2、题解：

1、假设先手，后手的状态是：, 当是胜利，等于0是失败，初始时石子数为,以及题目中的

2、首先如果最初始是1那必然先手必败，如果初始不为1，但是那么先手必胜，总的来说就是：

3、现在我们讨论else的情况，我们证明一定是由有连取机会的胜:

假设x拥有连取的机会，y没有，但是x输给了y

把x，y每个局面的操作抽象成点，构造成图，当如果找到一条x败给y的路径，也就是x再某个阶段一定处于必败态，因为每次操作必然是至少可以是1（奇数可以改变任何状态，偶数加 + 奇数 = 奇数，奇数 + 奇数 = 偶数），x必然可以先改变自己的状态为必胜态，此时所有输给y的路径都可以改变成必赢路径，所以必胜。

3、代码(cpp):

#include 
#define int long long 
using namespace std; 
constexpr int N = 1010;
int n, m, p; 

void solve() {
    cin >> n >> m >> p; 
    if(n == 1) {
        cout << "YangQiShaoNian" << endl;
        return;
    }
    else if(n == 2 || m >= n - 1) {
        cout << "XiaoNian" << endl; 
        return; 
    }
    else {
        if(p == 1) cout << "YangQiShaoNian" << endl; 
        else cout << "XiaoNian" << endl;
    }
}
signed main() {
    int ts = 1; 
    
    cin >> ts; 
        
    while(ts -- ) solve(); 
    
    return 0;
}

---

Part2  C题：

1、题意：

2、题解：

我们直接从p这个位置向两边模拟即可，每次维护最左边界和最右边界，时间复杂度最多是O(n * 10), 2e5的范围绰绰有余, 注意边界最后一定要是0和n + 1才能直接输出，否则只能是0。

3、代码(cpp)：

#include 
#define int long long 
using namespace std; 
constexpr int N = 1e6 + 10;
int n, p; 
int a[N], st[N];   
void solve() {
    cin >> n >> p; 
    for(int i = 0; i <= n + 1; i ++ ) a[i] = 0, st[i] = 0;
    for(int i = 1; i <= n; i ++ ) cin >> a[i];
    if(a[p] + 1 < 10) {
        cout << 0 << ' ' << 0 << endl;
        return; 
    }
    int l = p - 1, r = p + 1; 
    int lc = 1, rc = 1;
    int op = n * 11;
    while(op --) {
        if(lc + a[l] >= 10 && l >= 1) lc -= (10 - a[l]), a[l] = 10;  
        if(rc + a[r] >= 10 && r <= n) rc -= (10 - a[r]), a[r] = 10; 
        if(a[l] >= 10 && l >= 1) lc ++, rc ++, l --;
        if(a[r] >= 10 && r <= n) lc ++, rc ++, r ++;
    }
    if(l == 0) cout << lc << ' '; 
    else cout << 0 << ' '; 
    if(r == n + 1) cout << rc << endl; 
    else cout << 0 << endl;
//     cout << endl;
}
signed main() {
    int ts; 
    
    cin >> ts; 
        
    while(ts -- ) solve(); 
    
    return 0;
}

---

Part3  D题：

1、题意:

最初给定一个 每次可以朝着集合中添加 和, 并且a和b是独立的个体，构造一个得到的方案。

2、题解:

首先，这道题并不是可以任意构造的，因为时间是1秒，也就是构造一个尽量少步骤的方案，所以我们来挖掘一下一些性质：

 

此时我们得到了关键的东西，我们将其进行二进制拆解，是的各个二进制位。

据此，我们不妨先往集合中添加两个, 因为每次一个一个加非常数字非常大，考虑倍增优化:

此时我们不妨处理出来所有的二进制位上的数与的乘积，最后通过累加得到，也就是

3、代码(cpp):

#include 
#define int long long 
using namespace std; 
constexpr int N = 1e6 + 10;
int n, m; 
void solve() {
    int a, b; 
    cin >> a >> b; 
    if(a > b) swap(a, b); 
    if(b % a == 0) {
        cout << 0 << endl;
        return; 
    }
    int d = __gcd(a, b); 
    int aim = a * b / d / d;  
    int c = -1, t = -1;
    int cnt = 0; 
    for(int i = 0; i <= 62; i ++ )
        if(aim >> i & 1ll) {
            if(t == -1) t = i; 
            c = i;
            ++ cnt; 
    }
//     cout<= 2) {
        int state = d * (1ll << t);
        for(int i = t + 1; i < 62; i ++ ) {
            if(aim >> i & 1ll) { 
                cout << 2 << ' ' << state << ' ' << d * (1ll << i) << endl;
                state += d * (1ll << i); 
            }
        }
    }
    
}
signed main() {
    int ts; 
    
    cin >> ts; 
        
    while(ts -- ) solve(); 
    
    return 0;
}

感谢观看！