【题解】—— LeetCode一周小结4
【题解】—— 每日一道题目栏
上接:【题解】—— LeetCode一周小结3
22.最大交换
题目链接:670. 最大交换
给定一个非负整数,你至多可以交换一次数字中的任意两位。返回你能得到的最大值。
示例 1 :
输入: 2736
输出: 7236
解释: 交换数字2和数字7。
示例 2 :
输入: 9973
输出: 9973
解释: 不需要交换。
注意:
给定数字的范围是 [0, 108]
题解
方法:模拟
由题可知,我们应当将大的数放置在高位(首位),而当有数值相同的多个大数时,我们应当选择低位(末端)的数字。
因此,我们可以先将 num 的每一位处理出来存放到数组 list 中,随后预处理一个与 list 等长的数组 idx,带来代指 num 后缀中最大值对应的下标,即当 idx[i] = j 含义为在下标为 [0,i]位中 num[j]对应的数值最大。
同时由于我们需要遵循「当有数值相同的多个大数时,选择低位的数字」原则,我们应当出现采取严格大于才更新的方式来预处理 idx。
最后则是从高位往低位遍历,找到第一个替换的位置进行交换,并重新拼凑回答案。
class Solution {
public int maximumSwap(int num) {
List<Integer> list = new ArrayList<>();
while (num != 0) {
list.add(num % 10); num /= 10;
}
int n = list.size(), ans = 0;
int[] idx = new int[n];
for (int i = 0, j = 0; i < n; i++) {
if (list.get(i) > list.get(j)) j = i;
idx[i] = j;
}
for (int i = n - 1; i >= 0; i--) {
if (list.get(idx[i]) != list.get(i)) {
int c = list.get(idx[i]);
list.set(idx[i], list.get(i));
list.set(i, c);
break;
}
}
for (int i = n - 1; i >= 0; i--) ans = ans * 10 + list.get(i);
return ans;
}
}
方法:选择排序
我们可以从头开始遍历每一位,选出后面最大的数,如果这个最大的数比当前位置大,那就交换他们,但是,这个过程只能做一次。
class Solution {
public int maximumSwap(int num) {
if (num % 10 == num) return num;
char[] arr = String.valueOf(num).toCharArray();
for (int i = 0; i < arr.length; i++) {
// 从i后面选择一个最大的,这个最大的离i越远越好,比如1993,1交换第二个9更优,所以j倒序遍历
int maxIndex = i;
for (int j = arr.length - 1; j >= i + 1; j--) {
if (arr[j] > arr[maxIndex]) {
maxIndex = j;
}
}
if (maxIndex != i) {
char tmp = arr[i];
arr[i] = arr[maxIndex];
arr[maxIndex] = tmp;
return Integer.parseInt(new String(arr));
}
}
return num;
}
}
23.最长交替子数组
题目链接:2765. 最长交替子数组
给你一个下标从 0 开始的整数数组 nums 。如果 nums 中长度为 m 的子数组 s 满足以下条件,我们称它是一个 交替子数组 :
- m 大于 1 。
- s1 = s0 + 1 。
- 下标从 0 开始的子数组 s 与数组 [s0, s1, s0, s1,…,s(m-1) % 2] 一样。也就是说,s1 - s0 = 1 ,s2 - s1 = -1 ,s3 - s2 = 1 ,s4 - s3 = -1 ,以此类推,直到 s[m - 1] - s[m - 2] = (-1)m 。
请你返回 nums 中所有 交替 子数组中,最长的长度,如果不存在交替子数组,请你返回 -1 。
子数组是一个数组中一段连续 非空 的元素序列。
示例 1:
输入:nums = [2,3,4,3,4]
输出:4
解释:交替子数组有 [3,4] ,[3,4,3] 和 [3,4,3,4] 。最长的子数组为 [3,4,3,4] ,长度为4 。
示例 2:
输入:nums = [4,5,6]
输出:2
解释:[4,5] 和 [5,6] 是仅有的两个交替子数组。它们长度都为 2 。
提示:
2 <= nums.length <= 100
1 <= nums[i] <= 104
题解
分组循环
模板如下(可根据题目调整):
n = len(nums)
i = 0
while i < n:
start = i
while i < n and ...:
i += 1
# 从 start 到 i-1 是一组
# 下一组从 i 开始,无需 i += 1
适用场景:按照题目要求,数组会被分割成若干组,且每一组的判断/处理逻辑是一样的。
思路:
- 外层循环负责遍历组之前的准备工作(记录开始位置),和遍历组之后的统计工作(更新答案最大值)。
- 内层循环负责遍历组,找出这一组最远在哪结束。
这个写法的好处是,各个逻辑块分工明确,也不需要特判最后一组。以我的经验,这个写法是所有写法中最不容易出 bug 的,推荐大家记住。
对于本题来说,在内层循环时,假设这一组的第一个数是 333,那么这一组的数字必须形如 3,4,3,4,⋯,也就是nums[i]=nums[i−2]
另外,对于 [3,4,3,4,5,4,5] 这样的数组,第一组交替子数组为 [3,4,3,4],第二组交替子数组为 [4,5,4,5],这两组有一个数是重叠的,所以下面代码在外层循环末尾要把 i 减一。
class Solution {
public int alternatingSubarray(int[] nums) {
int ans = -1;
int i = 0, n = nums.length;
while (i < n - 1) {
if (nums[i + 1] - nums[i] != 1) {
i++; // 直接跳过
continue;
}
int i0 = i; // 记录这一组的开始位置
i += 2; // i 和 i+1 已经满足要求,从 i+2 开始判断
while (i < n && nums[i] == nums[i - 2]) {
i++;
}
// 从 i0 到 i-1 是满足题目要求的(并且无法再延长的)子数组
ans = Math.max(ans, i - i0);
i--;
}
return ans;
}
}
24.美丽塔 I
题目链接:2865. 美丽塔 I
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。
如果以下条件满足,我们称这些塔是 美丽 的:
- 1 <= heights[i] <= maxHeights[i]
- heights 是一个 山脉 数组。
如果存在下标 i 满足以下条件,那么我们称数组 heights 是一个 山脉 数组:
- 对于所有 0 < j <= i ,都有 heights[j - 1] <= heights[j]
- 对于所有 i <= k < n - 1 ,都有 heights[k + 1] <= heights[k]
请你返回满足 美丽塔 要求的方案中,高度和的最大值 。
示例 1:
输入:maxHeights = [5,3,4,1,1]
输出:13
解释:和最大的美丽塔方案为 heights = [5,3,3,1,1] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组,峰值在 i = 0 处。
13 是所有美丽塔方案中的最大高度和。
示例 2:
输入:maxHeights = [6,5,3,9,2,7]
输出:22
解释: 和最大的美丽塔方案为 heights = [3,3,3,9,2,2] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组,峰值在 i = 3 处。
22 是所有美丽塔方案中的最大高度和。
示例 3:
输入:maxHeights = [3,2,5,5,2,3]
输出:18
解释:和最大的美丽塔方案为 heights = [2,2,5,5,2,2] ,这是一个美丽塔方案,因为:
- 1 <= heights[i] <= maxHeights[i]
- heights 是个山脉数组,最大值在 i = 2 处。
注意,在这个方案中,i = 3 也是一个峰值。
18 是所有美丽塔方案中的最大高度和。
提示:
1 <= n == maxHeights <= 103
1 <= maxHeights[i] <= 109
题解
方法1:枚举
我们可以枚举每一座塔作为最高塔,每一次向左右两边扩展,算出其他每个位置的高度,然后累加得到高度和 t。求出所有高度和的最大值即可。
class Solution {
public long maximumSumOfHeights(List<Integer> maxHeights) {
long ans = 0;
int n = maxHeights.size();
for (int i = 0; i < n; ++i) {
int y = maxHeights.get(i);
long t = y;
for (int j = i - 1; j >= 0; --j) {
y = Math.min(y, maxHeights.get(j));
t += y;
}
y = maxHeights.get(i);
for (int j = i + 1; j < n; ++j) {
y = Math.min(y, maxHeights.get(j));
t += y;
}
ans = Math.max(ans, t);
}
return ans;
}
}
时间复杂度 O(n2),空间复杂度 O(1)。其中 n 为数组 maxHeights 的长度。
方法2:动态规划 + 单调栈
方法一的做法足以通过本题,但是时间复杂度较高。我们可以使用“动态规划 + 单调栈”来优化枚举的过程。
我们定义 f[i] 表示前 i+1 座塔中,以最后一座塔作为最高塔的美丽塔方案的高度和。我们可以得到如下的状态转移方程:
f [ i ] = { f [ i − 1 ] + h e i g h t s [ i ] , i f h e i g h t s [ i ] ≥ h e i g h t s [ i − 1 ] h e i g h t s [ i ] × ( i − j ) + f [ j ] , i f h e i g h t s [ i ] < h e i g h t s [ i − 1 ] f[i]=\left\{\begin{aligned} f[i−1]+heights[i], if heights[i]≥heights[i−1]\\ heights[i]×(i−j)+f[j],if heights[i]
其中 j 是最后一座塔左边第一个高度小于等于 heights[i] 的塔的下标。我们可以使用单调栈来维护这个下标。
我们可以使用类似的方法求出 g[i],表示从右往左,以第 i 座塔作为最高塔的美丽塔方案的高度和。最终答案即为 f[i]+g[i]−heights[i] 的最大值。
================================================
ps:动态规划形象理解的话就是,我们从左往右看:
情况1:依次递增,即heights[i]≥heights[i−1],符合美丽塔,把当前的heights[i]往上累加即可;
情况2:到i发现怎么不增反降了,即heights[i]<heights[i−1],由于对f[i]定义是把i作为峰,所以左侧比heights[i]高的要抹平到heights[i];
从左到右来一遍,从右到左来一遍,保证对每个i左右两边都符合以i为峰,最后求和再去重即可。
class Solution {
public long maximumSumOfHeights(List<Integer> maxHeights) {
int n = maxHeights.size();
Deque<Integer> stk = new ArrayDeque<>();
int[] left = new int[n];
int[] right = new int[n];
Arrays.fill(left, -1);
Arrays.fill(right, n);
for (int i = 0; i < n; ++i) {
int x = maxHeights.get(i);
while (!stk.isEmpty() && maxHeights.get(stk.peek()) > x) {
stk.pop();
}
if (!stk.isEmpty()) {
left[i] = stk.peek();
}
stk.push(i);
}
stk.clear();
for (int i = n - 1; i >= 0; --i) {
int x = maxHeights.get(i);
while (!stk.isEmpty() && maxHeights.get(stk.peek()) >= x) {
stk.pop();
}
if (!stk.isEmpty()) {
right[i] = stk.peek();
}
stk.push(i);
}
long[] f = new long[n];
long[] g = new long[n];
for (int i = 0; i < n; ++i) {
int x = maxHeights.get(i);
if (i > 0 && x >= maxHeights.get(i - 1)) {
f[i] = f[i - 1] + x;
} else {
int j = left[i];
f[i] = 1L * x * (i - j) + (j >= 0 ? f[j] : 0);
}
}
for (int i = n - 1; i >= 0; --i) {
int x = maxHeights.get(i);
if (i < n - 1 && x >= maxHeights.get(i + 1)) {
g[i] = g[i + 1] + x;
} else {
int j = right[i];
g[i] = 1L * x * (j - i) + (j < n ? g[j] : 0);
}
}
long ans = 0;
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, f[i] + g[i] - maxHeights.get(i));
}
return ans;
}
}
时间复杂度 O(n),空间复杂度 O(n)。其中 n 为数组 maxHeights的长度。
25.计算 K 置位下标对应元素的和
题目链接:2859. 计算 K 置位下标对应元素的和
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
请你用整数形式返回 nums 中的特定元素之 和 ,这些特定元素满足:其对应下标的二进制表示中恰存在 k 个置位。
整数的二进制表示中的 1 就是这个整数的 置位 。
例如,21 的二进制表示为 10101 ,其中有 3 个置位。
示例 1:
输入:nums = [5,10,1,5,2], k = 1
输出:13
解释:下标的二进制表示是:
0 = 0002
1 = 0012
2 = 0102
3 = 0112
4 = 1002
下标 1、2 和 4 在其二进制表示中都存在 k = 1 个置位。
因此,答案为 nums[1] + nums[2] + nums[4] = 13 。
示例 2:
输入:nums = [4,3,2,1], k = 2
输出:1
解释:下标的二进制表示是: 0 = 002
1 = 012
2 = 102
3 = 112
只有下标 3 的二进制表示中存在 k = 2 个置位。
因此,答案为 nums[3] = 1 。
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 105
0 <= k <= 10
题解
题目其实就是要计算一个整数列表中所有具有k个二进制位设置为1的索引的和。
位运算
把所有满足下标的二进制中的 1 的个数等于 k 的 nums[i] 加起来,就是答案。
class Solution {
public int sumIndicesWithKSetBits(List<Integer> nums, int k) {
int ans = 0, n = nums.size();
for (int i = 0; i < n; i++) {
if (Integer.bitCount(i) == k) {
ans += nums.get(i);
}
}
return ans;
}
}
时间复杂度:O(n),空间复杂度:O(1)。
问:Integer.bitCount(n)的时间复杂度究竟是O(1)还是O(log(n))?
答:是 O(1),无论 n 是 1 还是 1000000000 计算时间都是一样的。
大家也可以参考一下:java源码Integer.bitCount算法解析。
有关位运算的知识点,请看 从集合论到位运算,常见位运算技巧分类总结!
一行搞定
使用IntStream.range(0, nums.size())生成一个从0到nums.size()-1的整数流。然后,通过filter操作过滤出那些具有k个二进制位设置为1的索引。这是通过调用Integer.bitCount(x)来计算每个索引的二进制表示中1的数量,并与k进行比较实现的。最后,使用map操作将过滤后的索引映射回对应的整数值,并使用sum操作计算它们的总和。
class Solution {
public int sumIndicesWithKSetBits(List<Integer> nums, int k) {
return IntStream.range(0, nums.size())
.filter(x->k==Integer.bitCount(x))
.map(nums::get)
.sum();
}
}
26.边权重均等查询
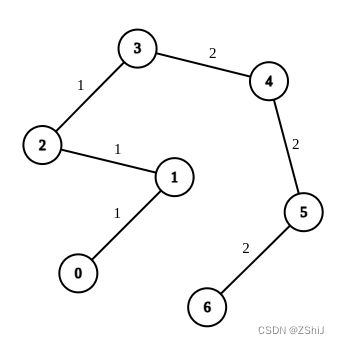
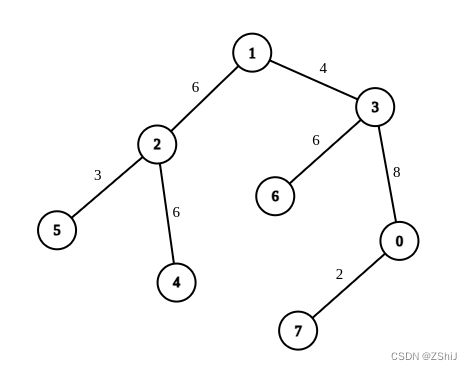
题目链接:2846. 边权重均等查询
现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。
另给你一个长度为 m 的二维整数数组 queries ,其中 queries[i] = [ai, bi] 。对于每条查询,请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中,你可以选择树上的任意一条边,并将其权重更改为任意值。
注意:
- 查询之间 相互独立 的,这意味着每条新的查询时,树都会回到 初始状态 。
- 从 ai 到 bi的路径是一个由 不同 节点组成的序列,从节点 ai 开始,到节点 bi 结束,且序列中相邻的两个节点在树中共享一条边。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是第 i 条查询的答案。
示例 1:
输入:n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]],
queries = [[0,3],[3,6],[2,6],[0,6]]输出:[0,0,1,3]
解释:第 1 条查询,从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此,答案为 0 。
第 2 条查询,从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 0 。
第 3 条查询,将边 [2,3] 的权重变更为 2 。在这次操作之后,从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为1 。
第 4 条查询,将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后,从节点 0 到节点 6的路径中的所有边的权重都是 2 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
输入:n = 8, edges =
[[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries =
[[4,6],[0,4],[6,5],[7,4]]输出:[1,2,2,3]
解释:第 1 条查询,将边 [1,3] 的权重变更为 6 。在这次操作之后,从节点 4 到节点 6 的路径中的所有边的权重都是 6。因此,答案为 1 。
第 2 条查询,将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后,从节点 0 到节点 4 的路径中的所有边的权重都是 6。因此,答案为 2 。
第 3 条查询,将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后,从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此,答案为 2 。
第 4 条查询,将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后,从节点 7 到节点 4的路径中的所有边的权重都是 6 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
提示:
题解
方法:倍增法求 LCA
题目求的是任意两点的路径上,将其所有边的权重变成相同值的最小操作次数。实际上就是求这两点之间的路径长度,减去路径上出现次数最多的边的次数。
而求两点间的路径长度,可以通过倍增法求 LCA 来实现。我们记两点分别为u 和 v,最近公共祖先为 x,那么 u 到 v 的路径长度就是 depth(u)+depth(v)−2×depth(x)
另外,我们可以用一个数组 cnt[n][26] 记录根节点到每个节点上,每个边权重出现的次数。那么 u 到 v 的路径上,出现次数最多的边的次数就是 max0≤j<26cnt[u][j]+cnt[v][j]−2×cnt[x][j]。其中 x 为 u 和 v 的最近公共祖先。
倍增法求 LCA 的过程如下:
我们记每个节点的深度为 depth,父节点为 p,而 f[i][j] 表示节点 i 的第 2j个祖先。那么,对于任意两点 x 和 y,我们可以通过以下方式求出它们的最近公共祖先:
- 如果 depth(x)
- 接下来,我们将 x 的深度不断向上提升,直到 x 和 y 的深度相同,此时 x 和 y 的深度都为 depth(x)d;
- 然后,我们将 x 和 y 的深度同时向上提升,直到 x 和 y 的父节点相同,此时 x 和 y 的父节点都为 f[x][0],即为 x 和 y 的最近公共祖先。
- 最后,节点 u 到节点 v 的最小操作次数就是 depth(u)+depth(v)−2×depth(x)−max0≤j<26cnt[u][j]+cnt[v][j]−2×cnt[x][j]。
class Solution {
public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {
int m = 32 - Integer.numberOfLeadingZeros(n);
List<int[]>[] g = new List[n];
Arrays.setAll(g, i -> new ArrayList<>());
int[][] f = new int[n][m];
int[] p = new int[n];
int[][] cnt = new int[n][0];
int[] depth = new int[n];
for (var e : edges) {
int u = e[0], v = e[1], w = e[2] - 1;
g[u].add(new int[] {v, w});
g[v].add(new int[] {u, w});
}
cnt[0] = new int[26];
Deque<Integer> q = new ArrayDeque<>();
q.offer(0);
while (!q.isEmpty()) {
int i = q.poll();
f[i][0] = p[i];
for (int j = 1; j < m; ++j) {
f[i][j] = f[f[i][j - 1]][j - 1];
}
for (var nxt : g[i]) {
int j = nxt[0], w = nxt[1];
if (j != p[i]) {
p[j] = i;
cnt[j] = cnt[i].clone();
cnt[j][w]++;
depth[j] = depth[i] + 1;
q.offer(j);
}
}
}
int k = queries.length;
int[] ans = new int[k];
for (int i = 0; i < k; ++i) {
int u = queries[i][0], v = queries[i][1];
int x = u, y = v;
if (depth[x] < depth[y]) {
int t = x;
x = y;
y = t;
}
for (int j = m - 1; j >= 0; --j) {
if (depth[x] - depth[y] >= (1 << j)) {
x = f[x][j];
}
}
for (int j = m - 1; j >= 0; --j) {
if (f[x][j] != f[y][j]) {
x = f[x][j];
y = f[y][j];
}
}
if (x != y) {
x = p[x];
}
int mx = 0;
for (int j = 0; j < 26; ++j) {
mx = Math.max(mx, cnt[u][j] + cnt[v][j] - 2 * cnt[x][j]);
}
ans[i] = depth[u] + depth[v] - 2 * depth[x] - mx;
}
return ans;
}
}
时间复杂度 O((n+q)×C×logn),空间复杂度 O(n×C×logn),其中 C 为边权重的最大值。
LCA 模板1
对于本题,由于 1≤wi≤26,我们可以在倍增的同时,维护从节点 x 到 x 的第 2i个祖先节点这条路径上的每种边权的个数。
对于每个询问,在计算 a 和 b 的最近公共祖先的同时,也同样地维护从 a 到 b 路径上的每种边权的个数 cnt。
我们可以让出现次数最多的边权保持不变,设其个数为 maxCnt,那么用从 a 到 b 路径长度减去 maxCnt,就得到了最小操作次数。
路径长度可以用深度数组 depth 算出,即(depth[a]−depth[lca])+(depth[b]−depth[lca])
其中 lca 是 a 和 b 的最近公共祖先,上式对应着一条在 lca 拐弯的路径。
注:另一种做法是维护从根到节点 x 的路径上的每种边权的出现次数,按照计算路径长度的思路,也可以通过加加减减算出路径上的每种边权的个数。
但是,如果把问题改成维护路径上的边权最大值,这种做法就不行了,而本题解的思路仍然是可以的。
class Solution {
public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {
List<int[]>[] g = new ArrayList[n];
Arrays.setAll(g, e -> new ArrayList<>());
for (var e : edges) {
int x = e[0], y = e[1], w = e[2] - 1;
g[x].add(new int[]{y, w});
g[y].add(new int[]{x, w});
}
int m = 32 - Integer.numberOfLeadingZeros(n); // n 的二进制长度
var pa = new int[n][m];
for (int i = 0; i < n; i++) {
Arrays.fill(pa[i], -1);
}
var cnt = new int[n][m][26];
var depth = new int[n];
dfs(0, -1, g, pa, cnt, depth);
for (int i = 0; i < m - 1; i++) {
for (int x = 0; x < n; x++) {
int p = pa[x][i];
if (p != -1) {
int pp = pa[p][i];
pa[x][i + 1] = pp;
for (int j = 0; j < 26; j++) {
cnt[x][i + 1][j] = cnt[x][i][j] + cnt[p][i][j];
}
}
}
}
var ans = new int[queries.length];
for (int qi = 0; qi < queries.length; qi++) {
int x = queries[qi][0], y = queries[qi][1];
int pathLen = depth[x] + depth[y];
var cw = new int[26];
if (depth[x] > depth[y]) {
int temp = x;
x = y;
y = temp;
}
// 让 y 和 x 在同一深度
for (int k = depth[y] - depth[x]; k > 0; k &= k - 1) {
int i = Integer.numberOfTrailingZeros(k);
int p = pa[y][i];
for (int j = 0; j < 26; ++j) {
cw[j] += cnt[y][i][j];
}
y = p;
}
if (y != x) {
for (int i = m - 1; i >= 0; i--) {
int px = pa[x][i];
int py = pa[y][i];
if (px != py) {
for (int j = 0; j < 26; j++) {
cw[j] += cnt[x][i][j] + cnt[y][i][j];
}
x = px;
y = py; // x 和 y 同时上跳 2^i 步
}
}
for (int j = 0; j < 26; j++) {
cw[j] += cnt[x][0][j] + cnt[y][0][j];
}
x = pa[x][0];
}
int lca = x;
pathLen -= depth[lca] * 2;
int maxCw = 0;
for (int i = 0; i < 26; i++) {
maxCw = Math.max(maxCw, cw[i]);
}
ans[qi] = pathLen - maxCw;
}
return ans;
}
private void dfs(int x, int fa, List<int[]>[] g, int[][] pa, int[][][] cnt, int[] depth) {
pa[x][0] = fa;
for (var e : g[x]) {
int y = e[0], w = e[1];
if (y != fa) {
cnt[y][0][w] = 1;
depth[y] = depth[x] + 1;
dfs(y, x, g, pa, cnt, depth);
}
}
}
}
时间复杂度:O((n+q)Ulogn),其中 q 为 queriess 的长度,U 为边权种类数。
空间复杂度:O(nUlogn)。返回值的长度不计入。
27.最大合金数
题目链接:2861. 最大合金数
假设你是一家合金制造公司的老板,你的公司使用多种金属来制造合金。现在共有 n 种不同类型的金属可以使用,并且你可以使用 k 台机器来制造合金。每台机器都需要特定数量的每种金属来创建合金。
对于第 i 台机器而言,创建合金需要 composition[i][j] 份 j 类型金属。最初,你拥有 stock[i] 份 i 类型金属,而每购入一份 i 类型金属需要花费 cost[i] 的金钱。
给你整数 n、k、budget,下标从 1 开始的二维数组 composition,两个下标从 1 开始的数组 stock 和 cost,请你在预算不超过 budget 金钱的前提下,最大化 公司制造合金的数量。
所有合金都需要由同一台机器制造。
返回公司可以制造的最大合金数。
示例 1:
输入:n = 3, k = 2, budget = 15, composition = [[1,1,1],[1,1,10]], stock
= [0,0,0], cost = [1,2,3]输出:2
解释:最优的方法是使用第 1 台机器来制造合金。
要想制造 2 份合金,我们需要购买:
- 2 份第 1 类金属。
- 2 份第 2 类金属。
- 2 份第 3 类金属。
总共需要 2 * 1 + 2 * 2 + 2 * 3 = 12 的金钱,小于等于预算 15 。
注意,我们最开始时候没有任何一类金属,所以必须买齐所有需要的金属。
可以证明在示例条件下最多可以制造 2 份合金。
示例 2:
输入:n = 3, k = 2, budget = 15, composition = [[1,1,1],[1,1,10]], stock
= [0,0,100], cost = [1,2,3]输出:5
解释:最优的方法是使用第 2 台机器来制造合金。
要想制造 5 份合金,我们需要购买:
- 5 份第 1 类金属。
- 5 份第 2 类金属。
- 0 份第 3 类金属。
总共需要 5 * 1 + 5 * 2 + 0 * 3 = 15 的金钱,小于等于预算 15 。
可以证明在示例条件下最多可以制造 5 份合金。
示例 3:
输入:n = 2, k = 3, budget = 10, composition = [[2,1],[1,2],[1,1]], stock
= [1,1], cost = [5,5]输出:2
解释:最优的方法是使用第 3 台机器来制造合金。
要想制造 2 份合金,我们需要购买:
- 1 份第 1 类金属。
- 1 份第 2 类金属。
总共需要 1 * 5 + 1 * 5 = 10 的金钱,小于等于预算 10 。
可以证明在示例条件下最多可以制造 2 份合金。
提示:
1 <= n, k <= 100
0 <= budget <= 108
composition.length == k
composition[i].length == n
1 <= composition[i][j] <= 100
stock.length == cost.length == n
0 <= stock[i] <= 108
1 <= cost[i] <= 100
题解
方法:二分
挨个判断每台机器最多可以制造多少份合金。
假设要制造 num 份合金,由于 num 越小,花费的钱越少,num 越多,花费的钱越多,有单调性,可以二分。
对于第 j 类金属:
- 如果
composition[i][j]⋅num≤stock[j],那么无需购买额外的金属。 - 如果
composition[i][j]⋅num>stock[j],那么需要购买额外的金属,花费为(composition[i][j]⋅num−stock[j])⋅cost[j]
遍历每类金属,计算总花费。如果总花费超过 budget,则无法制造 numm 份合金,否则可以制造。
最后讨论下二分的上下界:
- 二分上界:粗略计算一下,假设 composition[i][j] 和 cost[j] 都是 1,此时可以制造最多的合金,个数为
min(stock)+budget。 - 二分下界:可以设为 1。更巧妙的做法是,设当前答案为 ans,那么可以初始化二分下界为 ans+1,因为算出小于等于 ans 的值是没有意义的,不会让 ans 变大。如果这台机器无法制造出至少 ans+1份合金,那么二分循环结束后的结果为 ans,不影响答案。
下面的代码采用开区间写法,要把上界加一,下界减一。
// 全部转成 int[] 数组,效率比 List 更高
class Solution {
public int maxNumberOfAlloys(int n, int k, int budget, List<List<Integer>> composition, List<Integer> Stock, List<Integer> Cost) {
int ans = 0;
int mx = Collections.min(Stock) + budget;
int[] stock = Stock.stream().mapToInt(i -> i).toArray();
int[] cost = Cost.stream().mapToInt(i -> i).toArray();
for (List<Integer> Comp : composition) {
int[] comp = Comp.stream().mapToInt(i -> i).toArray();
int left = ans, right = mx + 1;
while (left + 1 < right) { // 开区间写法
int mid = left + (right - left) / 2;
boolean ok = true;
long money = 0;
for (int i = 0; i < n; i++) {
if (stock[i] < (long) comp[i] * mid) {
money += ((long) comp[i] * mid - stock[i]) * cost[i];
if (money > budget) {
ok = false;
break;
}
}
}
if (ok) {
left = mid;
} else {
right = mid;
}
}
ans = left;
}
return ans;
}
}
时间复杂度:O(knlogU),其中 U=min(stock)+budgetU。
空间复杂度:O(1)。
二分基础知识
二分的三种写法(闭区间、半闭半开区间、开区间)都是等价的,喜欢哪种就用哪种。
关于二分的基础知识,以及各种开闭区间的写法,具体请看视频讲解。
二分算法题单
【题单】二分算法(二分答案/最小化最大值/最大化最小值/第K小)
28.水壶问题
题目链接:365. 水壶问题
有两个水壶,容量分别为 jug1Capacity 和 jug2Capacity 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 targetCapacity 升。
如果可以得到 targetCapacity 升水,最后请用以上水壶中的一或两个来盛放取得的 targetCapacity 升水。
你可以:
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例 1:
输入: jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
输出: true
解释:来自著名的 “Die Hard”
示例 2:
输入: jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
输出: false
示例 3:
输入: jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
输出: true
提示:
1 <= jug1Capacity, jug2Capacity, targetCapacity <= 106
题解
方法一:深度优先搜索
首先对题目进行建模。观察题目可知,在任意一个时刻,此问题的状态可以由两个数字决定:X 壶中的水量,以及 Y 壶中的水量。
在任意一个时刻,我们可以且仅可以采取以下几种操作:
- 把 X 壶的水灌进 Y 壶,直至灌满或倒空;
- 把 Y 壶的水灌进 X 壶,直至灌满或倒空;
- 把 X 壶灌满;
- 把 Y 壶灌满;
- 把 X 壶倒空;
- 把 Y 壶倒空。
因此,本题可以使用深度优先搜索来解决。搜索中的每一步以 remain_x, remain_y 作为状态,即表示 X 壶和 Y 壶中的水量。在每一步搜索时,我们会依次尝试所有的操作,递归地搜索下去。这可能会导致我们陷入无止境的递归,因此我们还需要使用一个哈希结合(HashSet)存储所有已经搜索过的 remain_x, remain_y 状态,保证每个状态至多只被搜索一次。
在实际的代码编写中,由于深度优先搜索导致的递归远远超过了 Python 的默认递归层数(可以使用 sys 库更改递归层数,但不推荐这么做),因此下面的代码使用栈来模拟递归,避免了真正使用递归而导致的问题。
class Solution {
public boolean canMeasureWater(int x, int y, int z) {
Deque<int[]> stack = new LinkedList<int[]>();
stack.push(new int[]{0, 0});
Set<Long> seen = new HashSet<Long>();
while (!stack.isEmpty()) {
if (seen.contains(hash(stack.peek()))) {
stack.pop();
continue;
}
seen.add(hash(stack.peek()));
int[] state = stack.pop();
int remain_x = state[0], remain_y = state[1];
if (remain_x == z || remain_y == z || remain_x + remain_y == z) {
return true;
}
// 把 X 壶灌满。
stack.push(new int[]{x, remain_y});
// 把 Y 壶灌满。
stack.push(new int[]{remain_x, y});
// 把 X 壶倒空。
stack.push(new int[]{0, remain_y});
// 把 Y 壶倒空。
stack.push(new int[]{remain_x, 0});
// 把 X 壶的水灌进 Y 壶,直至灌满或倒空。
stack.push(new int[]{remain_x - Math.min(remain_x, y - remain_y), remain_y + Math.min(remain_x, y - remain_y)});
// 把 Y 壶的水灌进 X 壶,直至灌满或倒空。
stack.push(new int[]{remain_x + Math.min(remain_y, x - remain_x), remain_y - Math.min(remain_y, x - remain_x)});
}
return false;
}
public long hash(int[] state) {
return (long) state[0] * 1000001 + state[1];
}
}
复杂度分析
时间复杂度:O(xy),状态数最多有 (x+1)(y+1) 种,对每一种状态进行深度优先搜索的时间复杂度为 O(1),因此总时间复杂度为 O(xy)。
空间复杂度:O(xy),由于状态数最多有 (x+1)(y+1) 种,哈希集合中最多会有 (x+1)(y+1) 项,因此空间复杂度为 O(xy)。
方法二:广度优先遍历
思路及算法
这一类游戏相关的问题,用人脑去想,是很难穷尽所有的可能的情况的。因此很多时候需要用到搜索算法。
搜索算法一般情况下是在「树」或者「图」结构上的「深度优先遍历」或者「广度优先遍历」。因此,在脑子里,更建议动手在纸上画出问题抽象出来的「树」或者「图」的样子。
在「树上的「深度优先遍历」就是「回溯算法」,在「图」上的「深度优先遍历」是「flood fill」 算法,深搜比较节约空间。这道题由于就是要找到一个符合题意的状态,我们用广搜就好了。这是因为广搜有个性质,一层一层像水波纹一样扩散,路径最短。
所谓状态,就是指当前的任务进行到哪个阶段了,可以用变量来表示,怎么定义状态有的时候需要一定技巧,这道题不难。这里分别定义两个水壶为 A 和 B,定义有序整数对 (a, b) 表示当前 A 和 B 两个水壶的水量,它就是一个状态。
题目说:
你允许:
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水,直到装满或者倒空
为了方便说明,我们做如下定义:
装满任意一个水壶,定义为「操作一」,分为:
(1)装满 A,包括 A 为空和 A 非空的时候把 A 倒满的情况;
(2)装满 B,包括 B 为空和 B 非空的时候把 B 倒满的情况。
清空任意一个水壶,定义为「操作二」,分为
(1)清空 A;
(2)清空 B。
从一个水壶向另外一个水壶倒水,直到装满或者倒空,定义为「操作三」,其实根据描述「装满」或者「倒空」就知道可以分为 4 种情况:
(1)从 A 到 B,使得 B 满,A 还有剩;
(2)从 A 到 B,此时 A 的水太少,A 倒尽,B 没有满;
(3)从 B 到 A,使得 A 满,B 还有剩余;
(4)从 B 到 A,此时 B 的水太少,B 倒尽,A 没有满。
因此,从当前「状态」最多可以进行 8 种操作,得到 8 个新「状态」,对这 8 个新「状态」,依然可以扩展,一直做下去,直到某一个状态满足题目要求。
广度优先遍历常见的写法有 2 种,由于这里不用求路径最短的长度,在出队的时候不用读取队列的长度。
- 从当前状态可以扩展出 8 种相邻的状态;
- 因为状态有重复,因此是一个有向且有环的图,在遍历的时候,需要判断该结点设置是否访问过;
- 有序整数对 (a, b) 可以自定义成一个私有的类;
- 图的遍历,可以使用「深度优先遍历」和「广度优先遍历」,因为状态空间很大,广搜是相对较快;
- 尽量剪枝,跳过不必要的搜索;
- 当然最快的是数学方法。
import java.util.ArrayList;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Objects;
import java.util.Queue;
import java.util.Set;
public class Solution {
public boolean canMeasureWater(int x, int y, int z) {
// 特判
if (z == 0) {
return true;
}
if (x + y < z) {
return false;
}
State initState = new State(0, 0);
// 广度优先遍历使用队列
Queue<State> queue = new LinkedList<>();
Set<State> visited = new HashSet<>();
queue.offer(initState);
visited.add(initState);
while (!queue.isEmpty()) {
State head = queue.poll();
int curX = head.getX();
int curY = head.getY();
// curX + curY == z 比较容易忽略
if (curX == z || curY == z || curX + curY == z) {
return true;
}
// 从当前状态获得所有可能的下一步的状态
List<State> nextStates = getNextStates(curX, curY, x, y);
// 打开以便于观察,调试代码
// System.out.println(head + " => " + nextStates);
for (State nextState : nextStates) {
if (!visited.contains(nextState)) {
queue.offer(nextState);
// 添加到队列以后,必须马上设置为已经访问,否则会出现死循环
visited.add(nextState);
}
}
}
return false;
}
private List<State> getNextStates(int curX, int curY, int x, int y) {
// 最多 8 个对象,防止动态数组扩容,不过 Java 默认的初始化容量肯定大于 8 个
List<State> nextStates = new ArrayList<>(8);
// 按理说应该先判断状态是否存在,再生成「状态」对象,这里为了阅读方便,一次生成 8 个对象
// 以下两个状态,对应操作 1
// 外部加水,使得 A 满
State nextState1 = new State(x, curY);
// 外部加水,使得 B 满
State nextState2 = new State(curX, y);
// 以下两个状态,对应操作 2
// 把 A 清空
State nextState3 = new State(0, curY);
// 把 B 清空
State nextState4 = new State(curX, 0);
// 以下四个状态,对应操作 3
// 从 A 到 B,使得 B 满,A 还有剩
State nextState5 = new State(curX - (y - curY), y);
// 从 A 到 B,此时 A 的水太少,A 倒尽,B 没有满
State nextState6 = new State(0, curX + curY);
// 从 B 到 A,使得 A 满,B 还有剩余
State nextState7 = new State(x, curY - (x - curX));
// 从 B 到 A,此时 B 的水太少,B 倒尽,A 没有满
State nextState8 = new State(curX + curY, 0);
// 没有满的时候,才需要加水
if (curX < x) {
nextStates.add(nextState1);
}
if (curY < y) {
nextStates.add(nextState2);
}
// 有水的时候,才需要倒掉
if (curX > 0) {
nextStates.add(nextState3);
}
if (curY > 0) {
nextStates.add(nextState4);
}
// 有剩余才倒
if (curX - (y - curY) > 0) {
nextStates.add(nextState5);
}
if (curY - (x - curX) > 0) {
nextStates.add(nextState7);
}
// 倒过去倒不满才倒
if (curX + curY < y) {
nextStates.add(nextState6);
}
if (curX + curY < x) {
nextStates.add(nextState8);
}
return nextStates;
}
private class State {
private int x;
private int y;
public State(int x, int y) {
this.x = x;
this.y = y;
}
public int getX() {
return x;
}
public int getY() {
return y;
}
@Override
public String toString() {
return "State{" +
"x=" + x +
", y=" + y +
'}';
}
@Override
public boolean equals(Object o) {
if (this == o) {
return true;
}
if (o == null || getClass() != o.getClass()) {
return false;
}
State state = (State) o;
return x == state.x &&
y == state.y;
}
@Override
public int hashCode() {
return Objects.hash(x, y);
}
}
public static void main(String[] args) {
Solution solution = new Solution();
int x = 3;
int y = 5;
int z = 4;
// int x = 2;
// int y = 6;
// int z = 5;
// int x = 1;
// int y = 2;
// int z = 3;
boolean res = solution.canMeasureWater(x, y, z);
System.out.println(res);
}
}
方法三:数学
思路及算法
预备知识:贝祖定理
我们认为,每次操作只会让桶里的水总量增加 x,增加 y,减少 x,或者减少 y。
你可能认为这有问题:如果往一个不满的桶里放水,或者把它排空呢?那变化量不就不是 x 或者 y 了吗?接下来我们来解释这一点:
-
首先要清楚,在题目所给的操作下,两个桶不可能同时有水且不满。因为观察所有题目中的操作,操作的结果都至少有一个桶是空的或者满的;
-
其次,对一个不满的桶加水是没有意义的。因为如果另一个桶是空的,那么这个操作的结果等价于直接从初始状态给这个桶加满水;而如果另一个桶是满的,那么这个操作的结果等价于从初始状态分别给两个桶加满;
-
再次,把一个不满的桶里面的水倒掉是没有意义的。因为如果另一个桶是空的,那么这个操作的结果等价于回到初始状态;而如果另一个桶是满的,那么这个操作的结果等价于从初始状态直接给另一个桶倒满。
因此,我们可以认为每次操作只会给水的总量带来 x 或者 y 的变化量。因此我们的目标可以改写成:找到一对整数 a,b,使得ax+by=z ,而只要满足 z≤x+y,且这样的 a,b 存在,那么我们的目标就是可以达成的。这是因为:
-
若 a≥0,b≥0,那么显然可以达成目标。
-
若 a<0,那么可以进行以下操作:
1.往 y 壶倒水;
2.把 y 壶的水倒入 x 壶;
3.如果 y 壶不为空,那么 x 壶肯定是满的,把 x 壶倒空,然后再把 y 壶的水倒入 x 壶。
重复以上操作直至某一步时 x 壶进行了 aaa 次倒空操作,y 壶进行了 bbb 次倒水操作。 -
若 b<0b\lt 0b<0,方法同上,x 与 y 互换。
而贝祖定理告诉我们,ax+by=z 有解当且仅当 z 是 x,y 的最大公约数的倍数。因此我们只需要找到 x,y 的最大公约数并判断 z 是否是它的倍数即可。
class Solution {
public boolean canMeasureWater(int x, int y, int z) {
if (x + y < z) {
return false;
}
if (x == 0 || y == 0) {
return z == 0 || x + y == z;
}
return z % gcd(x, y) == 0;
}
public int gcd(int x, int y) {
int remainder = x % y;
while (remainder != 0) {
x = y;
y = remainder;
remainder = x % y;
}
return y;
}
}
复杂度分析
时间复杂度:O(log(min(x,y))),取决于计算最大公约数所使用的辗转相除法。
空间复杂度:O(1),只需要常数个变量。
下接:【题解】—— LeetCode一周小结5
请看 视频讲解 第四题,或者阅读【模板讲解】树上倍增算法(以及最近公共祖先) ↩︎