你真的了解操作符的魅力吗
今天我们来了解一下两个操作符的巧妙运用,解决一些题目。哪两个操作符呢?即:& 和 ^
在一个整型数组中,只有一个数字出现一次,其他数组都是成对出现的,请找出那个只出现一次的数字。
例如:
数组中有:1 2 3 4 5 1 2 3 4,只有5出现一次,其他数字都出现2次,找出5
相信大家看到这个问题,觉得很简单,我当初也是这样觉得,框框写了一个代码出来,但有的解法是更加的巧妙,下面我先写出我当初一开始写的代码,慢慢分析!
第一种方法:
int function(int arr[],int n)
{
int c,i=0;
while (i这便是我当初写下的代码,我就简单说一下,就是将数组和数组长度传入定义的函数function上,然后借助两个循环,和第三变量c,将c每次进循环时初始化为0,当循环过程中除本身外还有其他元素跟arr[ i ]相同时,我们就将c赋值为0,只有找到那个单身狗,即没有其它元素和它相同时 ,c==1,然后返回该元素的大小。
注意:改代码虽然容易想到但其最终过于复杂,代码不够整洁 。
第二种方法:
#include
int find_single_dog(int arr[], int sz)
{
int ret = 0;
int i = 0;
for (i = 0; i < sz; i++)
{
ret ^= arr[i];
}
return ret;
}
int main()
{
int arr[] = { 1,2,3,4,5,1,2,3,4 };
int sz = sizeof(arr) / sizeof(arr[0]);
int dog = find_single_dog(arr, sz);
printf("%d\n", dog);
return 0;
}
大家看这个代码就立马发现简洁了许多了呢,这又是基于什么原理呢,下面我们一一解剖,这个代码实现的原理。
首先我们要了解异或操作符,即"^",这个操作符,异或操作符有什么作用呢,我们可以用一个口诀来理解“相异为一,相同为0”,比如3^7=4,我们可以看一下图,来理解。
了解完异或,我们很容易就知道这两个式子了吧!
a^a=0 ------------两个相等的数他们32个bit位肯定是处处相等,那异或的结果 也就为32个bit位都为0了。
a^0=a ------------这也很容易想出来呢,只要a的一个bit位为1跟0肯定是相异,所以为1,所以就等于它本身了。
有了这两个式子,再看看上面第二种方法是不是就瞬间通透来了,只要ret不断异或数组中的所有元素,又如题目除了一个元素,其他都是成对出现的,以至于连个相同的数异或全为0,0异或一个数又等于他本身,所以ret最后只会是那一个单数,即题目说的单身狗。
接下来我们再看一题
在不创建临时变量的情况下,交换两个变量的值。
第一种方法:
int main()
{
int a = 4;
int b = 7;
printf("交换前:a=%d b=%d\n", a, b);
a = a + b;
b = a - b;
a = a - b;
printf("交换后:a=%d b=%d\n", a, b);
return 0;
}这个代码的原理为把两个数相加得到总合,再减去一个数就可以得到另一个数。
缺点:如果a+b的值太大会导致一个int类型的变量会无法储存下这个值,具有可能会使程序出错。
为了优化这个代码,我们来看第二种。
第二种方法:
int main()
{
int a = 7;
int b = 8;
printf("交换前:a=%d b=%d\n", a, b);
a = a ^ b;
b = a ^ b;
a = a ^ b;
printf("交换后:a=%d b=%d\n", a, b);
return 0;
}
这个代码就很好的优化了,刚刚说的储存问题。
原理:也是运用了上述所说的那两个式子a^a=0,a^0=a,通过先不断异或本身和0,实现两个变量的转换值。
写一个函数返回参数二进制中 1 的个数。
比如: 15 0000 1111 4 个 1
第一种方法:
int Find1(int n)
{
int count = 0;
while (n)
{
if (n % 2 == 1)
count++;
n = n / 2;
}
return count;
}
int main()
{
int n = 0;
scanf("%d", &n);
int count = Find1(n);
printf("%d\n", count);
return 0;
}我们都知道再二进制中每个比特位向左一位就是乘以2,向右移就是除以2,所以这个方法不断除2,在过程中只要n%2==1,则说明左右边一位为1,count++,然后继续除2,将比特位继续右移。
缺点:这种方法进行了大量的除法运算,使得代码的实现效率并不是很高。
第二种方法:
int Find1(unsigned int n)
{
int count = 0;
int i = 0;
for (i = 0; i < 32; i++)
{
if (((n >> i) & 1) == 1)
count++;
}
return count;
}
int main()
{
int n = 0;
scanf("%d", &n);
int count = Find1(n);
printf("%d\n", count);
return 0;
}原理:与第一种很相似,都是将32个比特位不断右移,但右移却是用的操作符“>>”进行右移,且每次循环检验最右边的比特位是否为1,为1,则count++,进行计数。这个方法相比于第一种略微要快。
缺点:无论如何都需要进行32次循环,效率还不算太高。
第三种方法:
int Find1(int n)
{
int count = 0;
while (n)
{
n = n & (n - 1);
count++;
}
return count;
}
int main()
{
int n = 0;
scanf("%d", &n);
int count = Find1(n);
printf("%d\n", count);
return 0;
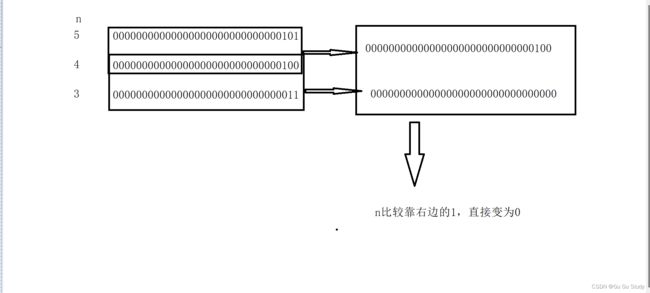
}大家要想弄懂原理那必须弄懂n=n&(n-1)这个代码的作用,那么我们先解释操作符"&",这个操作符相信大家都有所了解就是按位与,那么 n=n&(n-1),有什么作用呢
,我们看一下图。
这样就很明了,n=n&(n-1),就是将靠右的1,一个一个通过这个式子消除,这样有多少个1,就只需要进行多少次循环。效率也就变得比较高效了。