启发式合并

启发式合并

首先我们来考虑这样一个问题:
给定$n$个集合,每个集合的大小为$S$，${\sum }_{i=1}^n|S_{}i|==n$ 且各个集合里面没有相同的元素。问：每次把指定的两个集合，共合并$n-1$次，返回这个大集合

答：如果每次随意指定两个集合合并，那么最坏情况下每次直接把前一个集合合并到后一个集合上，就像是不断把大山搬到小山上面，那么遍历的时间复杂度是$O(n^2)$的，这样的速度并不理想，那么启发式合并就闪亮登场了

启发式合并：我们合并两个集合 $s1,s2$ 时，若 $|s1|<|s2|$ ，则将 $s1$ 中的元素加入 $s2$ ，这看上去好像没有什么优化是吧？但是实际上合并两个集合时，若元素属于较小的集合，那么它会被合并到较大的集合中。若一个元素被转移，则它所处的集合的大小至少变成了原来的两倍。假设总集合大小的上限是 $n$ ，则$1$个元素最多被转移 $\log n$ 次，$n$个元素最多被转移 $n\log n$ 次，所以启发式合并 的时间复杂度是 $O(n\log n)$ 的。

(这里有一个前提:集合 $s1,s2$之间没有相同元素，所以每次合并的时候集合大小至少变大为原来两倍，但是有相同的时候就不是两倍了，但是实际上不管有没有元素相同，假设所有集合的总大小为$m$，$O(m\log m)$ 的时间复杂度都是成立的，甚至有相同元素还会更快，这里可以思考一下不做证明了 我不会 )感觉题目不同，各个集合里面的元素不同，时间复杂度也不同，算起来有点玄学但是能过题就是了

对于启发式合并的应用，最常见的就是按秩合并了，比如可持久化并查集

		if(depx<depy){
			modify(1,n,rootfa[ver-1],rootfa[ver],x,y);
			rootdep[ver]=rootdep[ver-1];
		}

不断把深度小的树合并到深度大的树中，即把深度小的树的根节点指向深度大的树的根节点，可以证明最终树的深度为$logn$级别，这样我们就可以在$logn$时间里面找到任意节点的根节点了

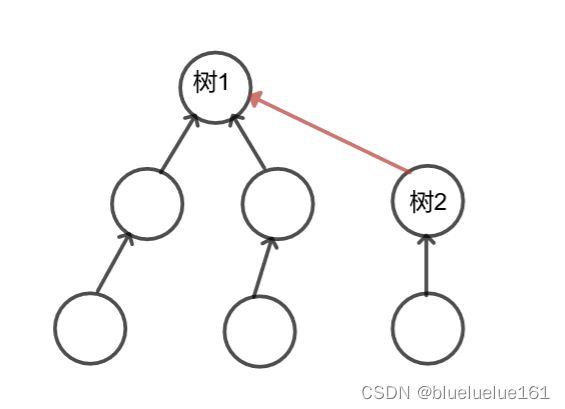
Educational Codeforces Round 132 E *2400
可持久化并查集维护的set是，对于节点$u$要用到的set是根节点到自己的简单路径的xor值+以及各个子树的，从根节点到子树里面的节点简单路径的xor值，然后启发式把子节点的set合并上来即可，合并途中判断子节点之间是否会形成违法路径形成的话最后把u赋值为inf然后清空s[u]集合（因为把u赋为inf后对于树更上面的节点来说就不可能形成违法路径了）

#include
#define int long long
#define io ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int maxn=2e5+5;
const int inf=1e9+7;
const int mod=1e9+7;
vector<int>vec[maxn];
int a[maxn];
int ans=0;
int pre[maxn];
set<int>s[maxn];
int d[maxn];
void dfs(int u,int fa){
	pre[u]=u;
	d[u]=d[fa]^a[u];
	s[pre[u]].insert(d[u]);
	int check=0;
	for(int v:vec[u]){
		if(v==fa){
			continue;
		}
		else{
			dfs(v,u);
			if(s[pre[v]].size()>s[pre[u]].size()){
				swap(s[pre[v]],s[pre[u]]);
			}
			for(int need:s[pre[v]]){
				if(s[pre[u]].find(need^a[u])!=s[pre[u]].end()){
					check=1;
				}
			}
			for(int need:s[pre[v]]){
				s[pre[u]].insert(need);
			}
		}
	}
	if(check){
		s[u].clear();
		ans++;
	}
}
void solve(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		vec[u].push_back(v);
		vec[v].push_back(u);
	}
	dfs(1,0);
	cout<<ans<<"\n";
}
signed main(){
	int t=1;
//	cin>>t;
	while(t--){
		solve();
	}
}

好路径的数目
如果直接暴力合并，在只有一层的时候不容易发现启发式合并的用处,比如这张图我们启发式合并和暴力把v合并到u上面好像并没有什么区别

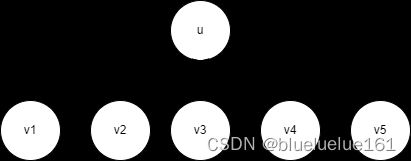
但是让我们考虑这样一种情况，树是一条链，每次直接子节点v向父节点u合并的话，那么是不是就变成大山搬小山了？所以用启发式合并优化

用map[u]记录以u为根节点时各个u->x的路径上x为最大值的x是那些，比方说1->3->2->4->4，那么记录下来的就有1为1，3为1，4为2，然后把子节点的map里面小于a[u]的值给后，根据size大小启发式合并上来即可

class Solution {
public:
static const int maxn=3e4+5;
vector<int>vec[maxn];
int ans[maxn];
map<int,int>mp[maxn];
int a[maxn];
void dfs(int u,int fa){
	ans[u]=1;
	mp[u][a[u]]++;
	for(int v:vec[u]){
		if(v==fa){
			continue;
		}
		else{
			dfs(v,u);
			ans[u]+=ans[v];
			for(auto it=mp[v].begin();it!=mp[v].end()&&it->first<a[u];){
				mp[v].erase(it++);
			}
			if(mp[v].size()>mp[u].size()){
				swap(mp[u],mp[v]);
			}
			for(auto it=mp[v].begin();it!=mp[v].end();it++){
				ans[u]+=(it->second)*mp[u][it->first];
				mp[u][it->first]+=it->second;
			}
		}
	}
}
int numberOfGoodPaths(vector<int>& vals, vector<vector<int>>& edges) {
	for(int i=0;i<vals.size();i++){
		a[i+1]=vals[i];
	}
	for(auto it:edges){
		int u=it[0],v=it[1];
		u++;
		v++; 
		vec[u].push_back(v);
		vec[v].push_back(u);
	}
	dfs(1,0);
	return ans[1];
}
};

2022牛客多校第一场J题
假设把点a作为起始点变成黑色激活后，把x,y,z这些点激活了，那么把已经变为黑色的点看成一个集合，那么这些集合的出边也是由a激活，即一个集合的，比方说假设x->k有一条边，那么把x->k这条边删掉，加上a->k这条边，然后把入度为1的点加入集合，这样处理就等价于儿子集合唯一入度为父亲集合，在中间合并出边的时候启发式合并即可

#include
using namespace std;
#define int long long
#define ll long long
#define vi vector<int> 
#define fi first
#define se second
#define pii pair<int,int>
#define pb push_back
#define all(v) v.begin(),v.end()
const double eps=1e-7;
const double pi=acos(-1);
const int N=2e5+5;
int pre[N];
set<int> jin[N],chu[N];
int find(int x){
	return x==pre[x]?x:pre[x]=find(pre[x]);
}
void mer(int x,int y){
	x=find(x),y=find(y);
	if(x==y) return;
	if(chu[x].size()<chu[y].size()) swap(x,y);
	vector<pii> v;
	for(auto j:chu[y]){
		chu[x].insert(j);
		if(jin[j].find(y)!=jin[j].end()) jin[j].erase(y);
		jin[j].insert(x);
	}
	pre[y]=x;
	for(auto j:chu[y]){
		if(jin[j].size()==1) mer(*jin[j].begin(),j);
	}
}
int sz[N];
signed main(){
	ios::sync_with_stdio(false);cin.tie(0);
	int __;
	cin>>__;
	for(int cas=1;cas<=__;cas++){
		int n;
		cin>>n;
		for(int i=1;i<=n;i++){
			pre[i]=i;jin[i].clear();chu[i].clear();sz[i]=0;
		}
		for(int i=1;i<=n;i++){
			int k;
			cin>>k;
			while(k--){
				int x;
				cin>>x;
				chu[x].insert(i);
				jin[i].insert(x);
			}
		}
		for(int i=1;i<=n;i++){
			if(jin[i].size()==1) mer(*jin[i].begin(),i);  //只有一个直接合并
		}
		for(int i=1;i<=n;i++) sz[find(i)]++;
		int ans=0;
		for(int i=1;i<=n;i++){
			ans=max(ans,sz[i]);
		}
		cout<<"Case #"<<cas<<": ";
		cout<<ans<<"\n";
	}
	return 0;
}

此外启发式合并还可以另辟蹊径解决一些问题

[HNOI2009] 梦幻布丁
思路：
这题有人的写法是手写链表，但是实际上用启发式合并也是可以的。
我们执行2操作时，就相当于把$x$合并到$y$里面，然后把$x$颜色的位置合并到$y$颜色的位置的集合里面，然后判断一下这些位置$i$修改颜色后对答案的影响，那么我们每次都把元素少的集合合并到元素多的集合里面，但是题目的限定是$x$->$y$，所以我们另用$now$数组映射一下真实颜色即可

#include
using namespace std;
const int  MAXN = 1000005;
vector<int>g[MAXN];
int n, m, op, x, y;
int ans = 0;
int col[MAXN], now[MAXN];
void _merge(int x, int y) {
	for (int i : g[x]) {
		if (col[i - 1] == y)ans--;
		if (col[i + 1] == y)ans--;
	}
	for (int i : g[x])col[i] = y;
	for (int i : g[x])g[y].push_back(i);
	g[x].clear();
}
void slove() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		cin >> col[i];
		now[col[i]] = col[i];
		if (col[i] != col[i - 1])ans++;
		g[col[i]].push_back(i);
	}
	while (m--) {
		cin >> op;
		if (op == 2)cout << ans << endl;
		else {
			cin >> x >> y;
			if (x == y)continue;
			//_merge(now[x], now[y]);
			if (g[now[x]].size() > g[now[y]].size()){
				_merge(now[y],now[x]);
				swap(now[x],now[y]);
			}
			else{
				_merge(now[x],now[y]);
				
			}
			
		}
	}
}
int main(){
	int t=1;
	while(t--){
		slove();
	}
}