算法设计与分析：分治法

目录

第1关：分治法介绍

任务描述：

相关知识：

基本概念：

解题步骤：

实例演示：

关键代码：

编程要求：

测试说明：

第2关：归并排序

任务描述：

相关知识：

问题描述：

归并排序解题步骤：

时间复杂度：

编程要求：

测试说明：

第3关：快速排序

任务描述：

相关知识：

简介：

问题描述：

快速排序：

时间复杂度：

快排科普：

编程要求：

测试说明：

第4关：中值问题

任务描述：

相关知识：

题目：

分析：

时间复杂度：

快排科普：

编程要求：

测试说明：

---

第1关：分治法介绍

任务描述：

本关任务：掌握分治法的基本原理，解决最大连续序列和问题。

相关知识：

为了完成本关任务，你需要掌握：分治法的基本原理。

基本概念：

分治法是构建基于多项分支递归的一种很重要的算法范式。字面上的解释是「分而治之」，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

分治法的适用场景：对于一个规模为 n 的问题，若该问题可以容易地解决（比如说规模 n 较小）则直接解决，否则将其分解为 k 个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

解题步骤：

分治算法解题一般分为三个步骤：

划分问题： 把问题的实例划分成子问题；

递归求解： 递归解决子问题；

合并问题： 合并子问题的解得到原问题的解。

为了帮助大家理解，下面我通过一个简单的实例，介绍分治法的求解思路和解题步骤。

实例演示：

最大序列和问题：给出一个长度为 n 的序列A1​,A2​,···,An​，求最大序列连续和。换句话说，要求找到 1<=i<=j<=n，使得Ai​+Ai+1​+···+Aj​尽量大。

假如现在有一组数[2，4，-2，1]，那么这组数的连续和有以下几种情况：

1. 2=2 [2]: 2
2. 4=4 [4]: 4
3. -2=-2 [-2]: -2
4. 1=1 [1]: 1
5. 2+4=6 [2,4]: 6
6. 4-2=2 [4,-2]:2
7. -2+1=-1 [-2,1]:-1
8. 2+4-2=4 [2,4,-2]:4
9. 4-2+1=3 [4,-2,1]:3
10. 2+4-2+1=5 [2,4,-2,1]:5

不难看出，组数[2，4，-2，1]的最大序列和为 6。这里采用的是穷举法，列举出了所有可能的结果，当数组长度比较大时，运算复杂度会非常大。

很容易看出，最大序列和问题适用于分治法。现在介绍一下如何用分治法来求解最大序列和问题，根据分治法的解题步骤，对应的解题思路如下：

• “划分”就是把序列分成元素个数尽量相等的左右两半；

• “递归求解”就是分别求出完全位于左半边或者完全位于右半边的最佳序列；

• “合并”就是求出起点位于左半、终点位于右半的最大连续和序列，并和子问题的最优解比较。

“划分”和“递归求解”基本上都能理解，关键在于“合并” 步骤。既然起点位于左半，终点位于右半，则可以认为把这样的序列分成两个部分，然后独立求解：先寻找最佳起点，然后再寻找最佳终点。

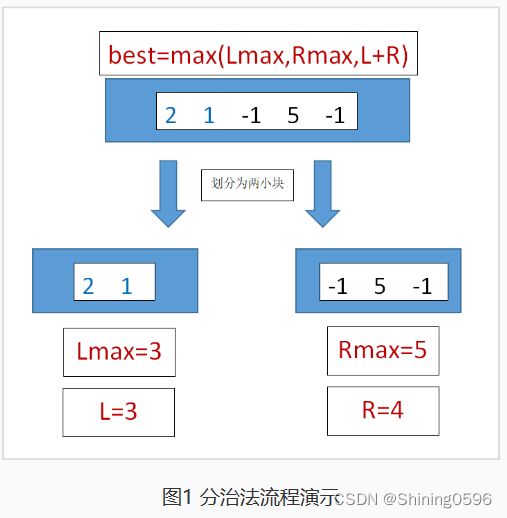
这里要求一组数的最大序列和，我们可以把数组分成两半，求另外两半数据的最大序列和，如果还是不能够解决问题，我们就再分两半，直到我们很容易做出判断为止，此时我们的“划分”，“递归求解”结束。例如：[2，1，-1，5，-1]，第一次“划分”后分成了两小块[2，1] 和 [-1，5，-1]；很容易看出，[2，1]小块的最大序列和是为3，[-1，5，-1]小块的最大序列和是3。那么[2，1，-1，5，-1]的最大序列和是多少呢？我们肉眼可见就是7。下面讲述一下“合并的过程”！

首先，我们需要明确一点，最大序列和有三种情况：

1.分两半之后，左边的最大序列和（简写“Lmax”）直接是整个序列的最大连续和；

2.分两半之后，右边的最大序列和（简写“Rmax”）直接是整个序列的最大连续和；

3.分两半之后，整个序列的最大连续和是整个序列的中间部位（简写“L+R”），即最大连续和包含左边的一部分数据和右边的一部分数据。

由上可得，[2，1，-1，5，-1]的最大连续序列和 = MAX(Lmax，Rmax，L+R)。

其次，我们要确定每次“划分”的分界点，这里用 m 表示，计算公式如下所示：

m=(序列长度-序列第一个值的索引)/2 # m 需要取整

例如：数组[2，1，-1，5，-1]第一次“划分”时，序列长度是 5，第一个序列值是 2，它的索引是 0。由公式可得，m=(5-0)/2=2 （需要取整）。

在“划分”时，遵循“左开右闭”的规则。以数组[2，1，-1，5，-1]为例，第一次“划分”的 m 值为 2，根据“左开右闭”的规则，可以划分为两小块[2，1] 和 [-1，5，-1]，即索引值为 2 的值被右小块取到了。

然后，需要依次求取 Lmax、Rmax、L 和 R 的值：

 最后，进行合并求解，best=max(Lmax，Rmax，L+R)=max(3,5,3+4)=7。这里没有进行递归演示，其实在求解右小块[-1，5，-1]的 Rmax 值时，用到了公式best=max(Lmax，Rmax，L+R)。

关键代码：

经上面的演算，分治法的 C++ 代码直接推导为：

int maxsum(int* A,int x,int y){  // 返回数组在左闭右开区间[x,y)中最大连续和
    int v,L,R,maxs;
    if(y-x==1) return A[x];  // 只有一个元素，直接返回
    int m=x+(y-x)/2;  // 分治第一步：划分成[x,m)和[m,y)
    maxs=max(maxsum(A,x,m),maxsum(A,m,y));  //  分治第二步：递归求解
    v=0;L=A[m-1];  //  分治第三步：合并(1)——从分界点开始往左的最大连续和L
    for(int i=m-1;i>=x;i--) L=max(L,v+=A[i]);
    v=0;  //分治第三步：合并(2)——从分界点开始往右的最大连续和R
    R=A[m];
    for(int i=m;i

数据结构、算法嘛！讲究效率。虽然对于最大序列和问题，用分治法相比于传统的方法看上去很巧妙，时间复杂度上也还过得去，分治法的时间复杂度是 O(n logn) 。但是对于这道题，分治法还不是最高效的，算法还可以再优化，时间复杂度可以达到 O(n) 。由于本章讲的是分治法，这里我就不做过多的阐述了。

编程要求：

根据提示，在右侧编辑器 Begin-End 区间补充代码，完成最大序列和问题的求解。

第一行一个数据n； 下面一行，有n个数字；

测试说明：

平台会对你编写的代码进行测试：

测试输入：

1. 4
2. 4 1 -4 2

说明：第一行为序列的长度，第二行为实际序列。

预期输出： 5

测试输入：

1. 4
2. 3 -4 -6 4

预期输出： 4

#include
#include
#include
#include
using namespace std;

int maxsum(int* A,int x,int y){  // 返回数组在左闭右开区间[x,y)中最大连续和
	/************ Begin ************/
    int v,l,r,maxs;
    if(y-x==1) return A[x];   //只有一个元素，直接返回
    int m = x + (y-x)/2; //分治第一步，划分为[x,m)和[m,y)
    maxs = max(maxsum(A,x,m),maxsum(A,m,y));//分治第二步：递归求解
    v=0;l=A[m-1];
    for(int i=m-1;i>=x;i--) l = max(l,v+=A[i]); // 分治第三步：合并（1）——从分界点开始往左的最大连续和L
    v=0;r=A[m];
    for(int i=m;i>n;
    for(int i=0;i>A[i];
    }
    cout<

第2关：归并排序

任务描述：

1. 理解 归并排序的算法原理 ;
2. 自己手动实现 归并排序。

相关知识：

为了完成本关任务，你需要掌握：为了完成本关任务，你需要掌握：分治法。

问题描述：

假设有 n 个整数，希望把它们按照从小到大的顺序排列，应该怎么做呢？可能第一想法，就是直接用C++的STL中的sort 或者stable_sort即可。可是，这些现成的排序函数是怎么样工作的呢？

下面我通过一个简单的排序对分治进行详解：

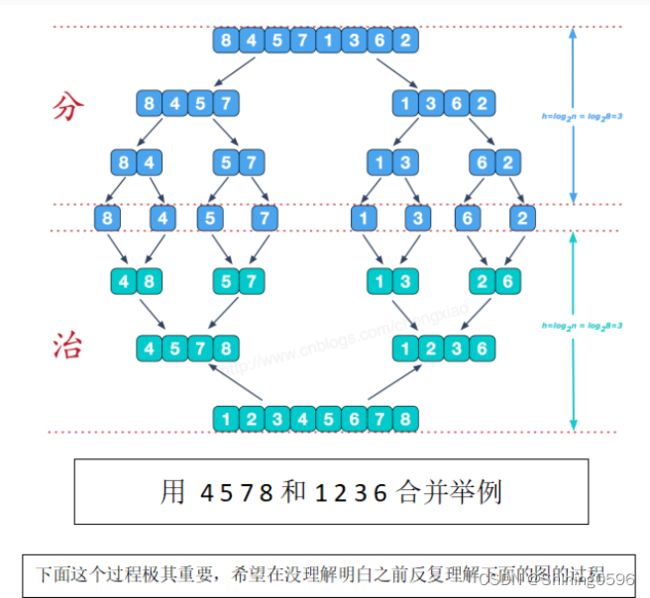
归并排序解题步骤：

分治算法解题一般分为三个步骤：

划分问题：把序列分成元素个数尽量相等的两半。

递归求解： 把两半元素分别排序。

合并问题： 把两个有序表合并成一个。

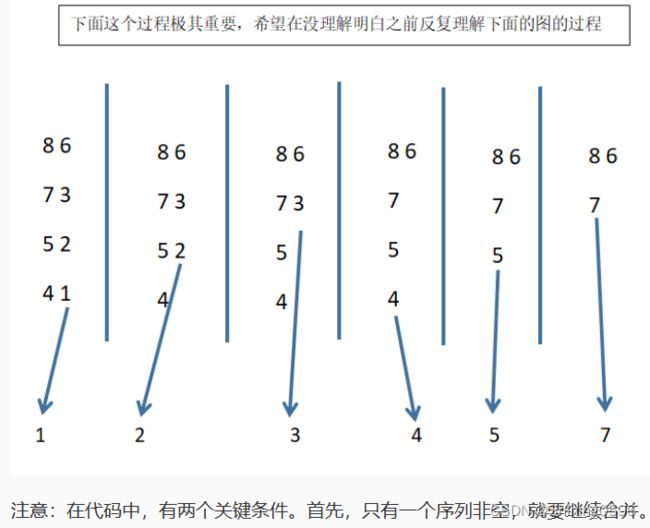
前面部分很容易完成。关键在于如何把两个有序表合成一个。下面有一个图，演示了一个合并的过程。每次只需要把两个序列的最小元素加以比较，删除其中较小元素并加入合并后的新表即可。由于需要一个新表来存放结果，所以附加空间为n。

 

 

注意：在代码中，有两个关键条件。首先，只有一个序列非空，就要继续合并。

• 如果第二个序列为空(此时第一个序列一定非空)，复制非空序列的最小元素
• 否则(第二序列非空)，当且仅当第一个序列也非空，且，第一个序列的最小值 <= 第二个序列的最小值时，才复制第一个序列的最小值 到 另外一个空间。

时间复杂度：

不难看出，归并排序的时间复杂度和最大连续和的分治算法一样，都是O(nlogn) 的。

编程要求：

根据提示，在右侧编辑器 Begin-End 区间补充代码，完成归并排序。

测试说明：

输入数据： 两行。第一行输入数字n。（有n个数待排序）； 第二行。有n个数。（待排序的n个数）。 输出数据： 一行。排好序的n个数。 平台会对你编写的代码进行测试：

测试输入：

1. 4
2. 3 1 2 4

预期输出：

1. 1 2 3 4

测试输入：

1. 5
2. 3 1 5 4 2

预期输出：

1. 1 2 3 4 5

#include 
using namespace std;

void merge_sort(int *A,int x,int y,int *B){
	// A 待排序数组；x 首索引；y 数组长度；B 附加空间 
	/********** Begin **********/
    if(y-x>1)
    {
        int m=x+(y-x)/2;
        int p=x,q=m,i=x;
        merge_sort(A,x,m,B);
        merge_sort(A,m,y,B);
        while(p=y||(p>n;
    for(int i=0;i>A[i];
    merge_sort(A,0,n,B);
    for(int i=0;i

第3关：快速排序

任务描述：

本关任务：

1. 理解 快速排序的算法原理 ;
2. 自己手动实现 快速排序。

相关知识：

为了完成本关任务，你需要掌握：c++基础。

简介：

快速排序是最快的通用内部排序算法。它由 Hoare 于1962年提出，相对于归并排序来说，不仅速度更快，并且不需要辅助空间。

问题描述：

输入 n 个整数和一个一个正整数k (1<=k<=n),输出这些整数从小到大排序。

 

 

快速排序：

按照分治三步法，将快速排序算法做如下介绍

划分问题：把左右两部分，使得左边任意元素都小于或等于右边任意元素。

递归求解：把左右两部分分别排序。

合并问题：不用合并，因为此时数组已经完全有序。

可能有人觉得这样子的描述太过笼统，分治算法最难的步骤合并都省去了，但事实上，快速排序本来就不是只有一种实现方法。“划分过程”有多个不同的版本，导致快速排序也有不同的版本。读者很容易在互联网啥该找到各种快速排序的版本。

下面，给出其中的一个版本。

假设现在对“6 1 2 7 9 3 4 5 10 8”这个 10 个数进行排序。首先在这个序列中随便找一个数作为基准数（不要被这个名词吓到了，就是一个用来参照的数，待会你就知道它用来做啥的了）。为了方便，就让第一个数 6 作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在 6 的右边，比基准数小的数放在 6 的左边，类似下面这种排列。

3 1 2 5 4 6 9 7 10 8

在初始状态下，数字 6 在序列的第 1 位。目标是将 6 挪到序列中间的某个位置，假设这个位置是 k。现在就需要寻找这个 k，并且以第 k 位为分界点，左边的数都小于等于 6，右边的数都大于等于 6。想一想，你有办法可以做到这点吗？

方法其实很简单：分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于 6 的数，再从左往右找一个大于 6 的数，然后交换他们。这里可以用两个变量 i 和 j，分别指向序列最左边和最右边。为这两个变量起个好听的名字“哨兵 i”和“哨兵 j”。刚开始的时候让哨兵 i 指向序列的最左边（即 i=1），指向数字 6。让哨兵 j 指向序列的最右边（即 j=10），指向数字 8。

首先哨兵 j 开始出动。因为此处设置的基准数是最左边的数，所以需要让哨兵 j 先出动，这一点非常重要（请自己想一想为什么）。哨兵 j 一步一步地向左挪动（即 **j--**），直到找到一个小于 6 的数停下来。接下来哨兵 i 再一步一步向右挪动（即 **i++**），直到找到一个数大于 6 的数停下来。最后哨兵 j 停在了数字 5 面前，哨兵 i 停在了数字 7 面前。

现在交换哨兵 i 和哨兵 j 所指向的元素的值。交换之后的序列如下。

6 1 2 5 9 3 4 7 10 8

到此，第一次交换结束。接下来开始哨兵 j 继续向左挪动（再友情提醒，每次必须是哨兵 j 先出发）。他发现了 4（比基准数 6 要小，满足要求）之后停了下来。哨兵 i 也继续向右挪动的，他发现了 9（比基准数 6 要大，满足要求）之后停了下来。此时再次进行交换，交换之后的序列如下。

6 1 2 5 4 3 9 7 10 8

第二次交换结束，“探测”继续。哨兵 j 继续向左挪动，他发现了 3（比基准数 6 要小，满足要求）之后又停了下来。哨兵 i 继续向右移动，糟啦！此时哨兵 i 和哨兵 j 相遇了，哨兵 i 和哨兵 j 都走到 3 面前。说明此时“探测”结束。将基准数 6 和 3 进行交换。交换之后的序列如下。

3 1 2 5 4 6 9 7 10 8

到此第一轮“探测”真正结束。此时以基准数 6 为分界点，6 左边的数都小于等于 6，6 右边的数都大于等于 6。回顾一下刚才的过程，其实哨兵 j 的使命就是要找小于基准数的数，而哨兵 i 的使命就是要找大于基准数的数，直到 i 和 j 碰头为止。

OK，解释完毕。现在基准数 6 已经归位，它正好处在序列的第 6 位。此时我们已经将原来的序列，以 6 为分界点拆分成了两个序列，左边的序列是“3 1 2 5 4”，右边的序列是“ 9 7 10 8 ”。接下来还需要分别处理这两个序列。因为 6 左边和右边的序列目前都还是很混乱的。不过不要紧，我们已经掌握了方法，接下来只要模拟刚才的方法分别处理 6 左边和右边的序列即可。

左边的序列是“3 1 2 5 4”。请将这个序列以 3 为基准数进行调整，使得 3 左边的数都小于等于 3，3 右边的数都大于等于 3。好了开始动笔吧。

如果你模拟的没有错，调整完毕之后的序列的顺序应该是。

2 1 3 5 4

OK，现在 3 已经归位。接下来需要处理 3 左边的序列“ 2 1 ”和右边的序列“5 4”。对序列“ 2 1 ”以 2 为基准数进行调整，处理完毕之后的序列为“1 2”，到此 2 已经归位。序列“1”只有一个数，也不需要进行任何处理。至此我们对序列“ 2 1 ”已全部处理完毕，得到序列是“1 2”。序列“5 4”的处理也仿照此方法，最后得到的序列如下。

1 2 3 4 5 6 9 7 10 8

对于序列“9 7 10 8”也模拟刚才的过程，直到不可拆分出新的子序列为止。最终将会得到这样的序列，如下。

1 2 3 4 5 6 7 8 9 10

到此，排序完全结束。细心的同学可能已经发现，快速排序的每一轮处理其实就是将这一轮的基准数归位，直到所有的数都归位为止，排序就结束了。

时间复杂度：

快速排序之所比较快，因为相比冒泡排序，每次交换是跳跃式的。每次排序的时候设置一个基准点，将小于等于基准点的数全部放到基准点的左边，将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是 **O(N2)**，它的平均时间复杂度为 **O(NlogN)**。

 

快排科普：

快速排序的时间复杂度为：最坏情况O(n2)；平均情况O(nlogn)，但实践中几乎不可能达到最坏情况，效率非常高。根据快速排序思想，可以在平均O(n)时间内选出数组中第 k 大的元素。

 

编程要求：

根据提示，在右侧编辑器补充代码，选出序列中第k大的元素。

测试说明：

输入数据： 两行。第一行输入数字n。（有n个数待排序）； 第二行。有n个数。（待排序的n个数）。 输出数据： 一行。排好序的n个数。

平台会对你编写的代码进行测试：

测试输入：

1. 4
2. 3 1 2 4

预期输出：

1. 1 2 3 4

测试输入：

1. 7
2. 4 7 5 3 6 2 1

#include
using namespace std;
const int maxn=20000;
int a[maxn];

void qsort(int l, int r)
{
	/*********** Begin **********/
    if(l >= r)
		return;
	int i = l, j = r;
	int key = a[r];
	while(i < j) {
		while(i < j && a[i] <= key)
			i++;//此处比较数值与key大小必须是<=，不然a[i]==key的情况下，i不变就造成死循环。  
		a[j] = a[i];//若没有=，遇到1122这样(含等值的项)的序列在两个相等的数比较时会造成死循环 
		while(i < j && a[j] >= key)
			j--;
		a[i] = a[j];
	}
	a[i] = key;
	qsort(i, r);
	qsort(l, i-1);
	/*********** End **********/
}

int main(){
	int n;
	cin>>n;
	for(int i=0;i>a[i];
	qsort(0,n-1);
	for(int i=0;i

第4关：中值问题

任务描述：

本关任务： 独立完成中值问题。

相关知识：

为了完成本关任务，你需要掌握：分治法。

题目：

输入 n 个整数和一个一个正整数k (1<=k<=n),输出这些整数从小到大排序后的第k个(例如，k=1就是最小值)。n<=107

分析：

备注(在数据结构算法中，解决问题的方法有很多，但是，请转变一个观念。不是达到目的就可以了。要考虑时间效率。如果在最短的时间内完成任务。)

选择第k大的数，最容易想到的方法是先排序，然后直接输出下标为k-1的元素(别忘了C语言中数组下标从0开始)，但107的规模即使对于O(nlogn)的算法来说较大。有没有更快的方法呢？

答案是肯定有的。假设在快速排序的“划分”结束后，数组A[l···r]被分成了A[l···q]和A[q,r]，则可以根据左边的元素个数q-l+1和 k的大小关系只在左边或者右边递归求解。

时间复杂度：

可以证明，在期望意义下，程序的时间复杂度为O(n)。

快排科普：

快速排序的时间复杂度为：最坏情况O(n2)；平均情况O(nlogn)，但实践中几乎不可能达到最坏情况，效率非常高。根据快速排序思想，可以在平均O(n)时间内选出数组中第 k 大的元素。

编程要求：

根据提示，在右侧编辑器补充代码，选出序列中第k大的元素。

测试说明：

输入数据： 两行。第一行输入数字n。（有n个数待排序）； 第二行。有n个数。（待排序的n个数）。 输出数据： 一个数。为n给数中第n大的数。 平台会对你编写的代码进行测试：

测试输入：

1. 4
2. 3 1 2 4
3. 3

预期输出：

1. 3

测试输入：

1. 7
2. 4 7 5 3 6 2 1
3. 3

预期输出： 3

#include
using namespace std;

int Partition(int low, int high, int a[])
{
	int temp = a[low];//基准点
	if (low < high)
	{
		while (low < high)
		{
			while (low < high && temp <=a[high]) //从后往前找到第一个比基准点大的
				high--;
			
			if (low < high)
				a[low] = a[high]; //放到基准点位置也就是第一个
				
			while (low < high && a[low] >n;
	int a[n];
	for(int i=0;i>a[i];
	int k,k_value;
	cin>>k;
	k_value=best_sort_k(a,0,n-1,k);
	cout<