蓝桥杯训练1

1 找哪个深度的节点权值最大

暴力

#include
using namespace std;
int main(){
    int n;
    cin>>n;
    int a[111];
    for(int i=1;i<=n;i++)
    cin>>a[i];
    int M=0;
    int t=0;
    int ans=0;
    int count=-1;
    for(int i=1;i<=n;i++)
    {
    if((int)(log2(i)+1)>count){
        count=(int)(log2(i)+1);
        ans=a[i];
    }
    else ans+=a[i];
    
    if(ans>M){
        M=ans;
        t=count;
    }

    }
    cout<<t;
    system("pause");
}

dfs
从根节点开始遍历，遍历途中记录每层的值，然后要注意权值可为负数并且数组越界的情况

#include
using namespace std;
#define MAX 300055
typedef long long ll;
ll w[MAX];
ll a[MAX];
void dfs(int x,int depth){
    if(x>n)return ;
     w[depth]+=a[x];
     dfs(x<<1,depth+1);
     dfs(x<<1+1,depth+1);
}
int main(){
    int n;
    int ans=-MAX,t=0;
    cin>>n;
    for(int i=1;i<=n;i++)
    cin>>a[i];
    dfs(1,1);
    for(int i=1;i<=n;i++)
    {
        if(w[i]>ans){
            ans=w[i];
            t=i;
        }
    }
    cout<<t;
    system("pause");
}

2.外卖店优先级

这题用vector数组会舒服清晰很多（同样能够sort排序），然后对每一家店进行判断，判断过程非常容易出错！首先怎么选择开始是个问题，我这里选择i=1开始，以外卖店now=2开局（如果只有一个订单不会执行循环，后续代码也能解决），然后每次把间隔时间求出来，now减去这个时间，当对now进行减操作，立即判断有没有踢出队列，最后加操作的时候也是立即判断有没有加入队列。最后就是把t减去最后的订单时间判定要不要T。总之，这题思路不清晰就非常容易出错

#include
using namespace std;
const int maxn = 100052;
typedef long long int qq;
vector<int>a[maxn];
int n,m,t;
bool f(int x){
  if(a[x].size()==0)return false;
  int now=2;
  int dis;
  int interval=0;
  int ret;
  for(int i=1;i<a[x].size();i++)
  {   
    dis=a[x][i]-a[x][i-1];
    if(dis!=0)now-=dis-1;//如果订单同一天，则不需要减
    if(now<=3)ret=0;//因为now可能减少了，直接判定
    now=max(0,now);
    now+=2;
    if(now>5)ret=1; 
  }

  int xx=now-(t-a[x][a[x].size()-1]);
  if(xx<=3)ret=0;
  return ret;
} 
int main(){
    scanf("%d%d%d",&n,&m,&t);
    while(m--){
        int ts,id;
        scanf("%d%d",&ts,&id);
        a[id].push_back(ts);
    }
    for(int i=1;i<=n;i++)
    {
        if(a[i].size()!=0)
        sort(a[i].begin(),a[i].end());
    }

    int ans=0;
    for(int i=1;i<=n;i++){
        if(f(i)==true)ans++;
    }
    printf("%d\n",ans);
      system("pause");
    return 0;
  
}

3.修改数组

思路是用并查集，一开始所有结点的父亲都设为自己，要保持的是，父亲节点的值代表没有出现过的值。
然后对输入的数组进行遍历，每做一次遍历，先让该值等于父亲结点的值，更新完之后，令这个节点的父亲的值进行加1.也就是这个节点的父亲的值被取了之后，要对其进行更新
总结一下：每次更新完一个结点后，他输出的值必定是他父亲的值，这个父亲的值之前没有被用过，但是现在被用了，就要+1，虽然+1不能保证+1的后的结果也未使用，但是即使被使用（f[i]!=i），下次遇到相同的x，通过find(x),能够找到祖先，这个祖先是一定未被使用的

#include
using namespace std;
int n;
int a[1234567];
int f[1234567];
int find(int x){
  return x==f[x]?x:f[x]=find(f[x]);
}
int main(){
  scanf("%d",&n);
  for(int i=1;i<1234567;i++)
  f[i]=i;
  for(int i=1;i<=n;i++)
  {
   scanf("%d",&a[i]);
    a[i]=find(a[i]);
    f[a[i]]=a[i]+1;

  }
  for(int i=1;i<=n;i++)
  printf("%d ",a[i]);
  system("pause");
  return 0;
};

4.糖果（状态压缩+dp）

状态压缩很好理解，dp这一块我看别人看了好久才弄懂，还是菜0.0，本质上是用已有的状态进行排列组合。

#include
using namespace std;
#define M 1<<20
int dp[(M)+5];//这里没加括号直接MLE
int state[101];
int main(){
    int n,m,k,s;
    int t;
    cin>>n>>m>>k;
    memset(dp,-1,sizeof(dp));
    for(int i=1;i<=n;i++)
    {   
         t=0;
        for(int j=1;j<=k;j++)
        {   
            cin>>s;
            t|=1<<(s-1);
        }
        state[i]=t;
        dp[state[i]]=1;
    }
    //dp[i]代表组成i状态需要多少包
    //这里的二层循环就是将n种状态排列组合，i每加1，dp中就多出一些组合，当i到n，所有组合都有了
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=(1<<m)-1;j++)
        {   if(dp[j]==-1)continue;//还没有出现的组合状态，直接跳出
            if(dp[state[i]|j]==-1)dp[state[i]|j]=dp[j]+1;//更新新出现的组合状态
            //加1的原因是所有的原生state都代表1次，所以只需要在dp[j]基础上加1
            else dp[state[i]|j]=min(dp[state[i]|j],dp[j]+1);
        }

    }
    cout<<dp[(1<<m)-1]<<endl;
    system("pause");
    return 0;
}

5.全球变暖dfs

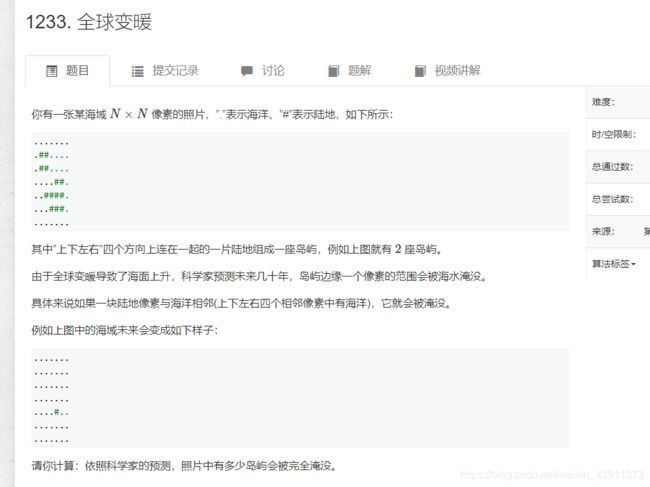
首先题目给的数据应该是外面一圈全是海，我是依照这个标准来写的。还有一块岛屿可能变化后会成为两块小岛，但是按照题目的意思好像它们还是算一块。所以我用a数组来记录岛屿的情况。每遇到一块未访问的陆地，就dfs遍历该陆地的整个连通分量，如果遇到符合情况的陆地，将该数组标记为1，即便遇到多块，还是1（根据题意以及样例）。最后连通分量数减去数组中为1的个数就是消失的岛屿数目

#include
using namespace std;
int n;
int cnt=0;
int ans=0;
int a[1234567];
char ma[1002][1002];
int vis[1002][1002];
void dfs(int i,int j){
if(i<=0||i>n||j<=0||j>n)return ;
if(vis[i][j]==1)return ;
if(ma[i][j]=='.')return ;
vis[i][j]=1;//这句话没加导致报错淦
if(ma[i][j+1]=='#'&&ma[i][j-1]=='#'&&ma[i-1][j]=='#'&&ma[i+1][j]=='#')
a[cnt]=1;

dfs(i+1,j);
dfs(i-1,j);
dfs(i,j+1);
dfs(i,j-1);


}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    {
        cin>>ma[i][j];
    }
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    {   
        if(ma[i][j]=='#'&&vis[i][j]==0)
        {              //每出现一块未访问的陆地，则作为新的连通分量进行搜索
            a[++cnt]=0;//用一个数组记录连通分量的状态
            dfs(i,j);
            


        }
  
    }
    for(int i=1;i<=cnt;i++)
    ans+=a[i];//所有剩下的连通分量
    //cnt就是之前的小岛数目
    cout<<cnt-ans<<endl;

    system("pause");
    return 0;
}

6.倍数问题

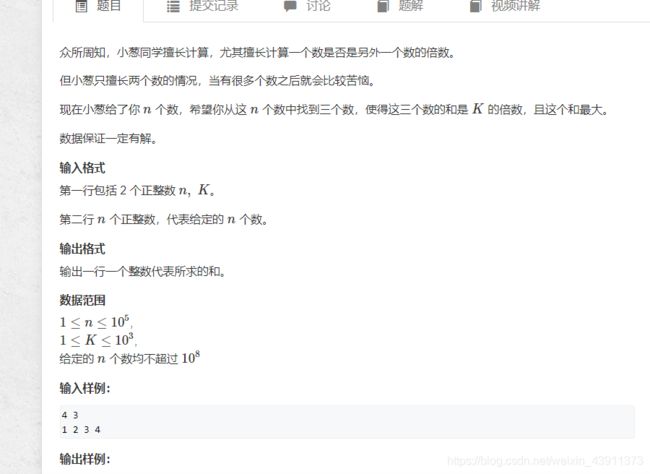
法一（dfs->tle）套用组合数的板子，n=1000的时候就T了

#include
using namespace std;
int st[100];
int top=0;
int n,m=3;
int k;
int a[123456];
int ans=0;
int sum=0;
void dfs(int depth){
    if(depth>n)return;//输入数组已经遍历完
                    //这里之前写==错了，用到最后一个数的时候是在depth==n的时候才输出的
    if(top==m) //输出条件
    {  
        sum=0;
       for(int i=0;i<m;i++)
            sum+=st[i];
        if(sum%k==0)
        ans=max(ans,sum);
        
        return;
    }
    st[top++]=a[depth];
    dfs(depth+1);
    top--;//抹掉之前状态，
    dfs(depth+1);
    return ;


}
int main(){
    cin>>n>>k;
    for(int i=0;i<n;i++)
    cin>>a[i];
    dfs(0);//a数组从0开始
    cout<<ans<<endl;
    system("pause");
    return 0;
}

7.付账问题

主要思路就是贪心，先排序，从最小的开始，如果最小的都能付，那么结果是是0。否则，当前面的少付，后面就要多付，后面的平均值就会提高，要让它们的值尽量接近这个变化的平均值。
我这里用了两个数组，我看了别人的，更简单的可以边判断边计算方差，如果不够就是avg-a[i]，如果够了就是avg-curavg。

#include
using namespace std;
    int n;
    double S;
    double a[500005]; //定义在main函数里报错我干
    double a1[500005];
    double ans=0;
    double avg;
int main(){
  
    cin>>n>>S;
    for(int i=1;i<=n;i++)
    cin>>a[i];
    sort(a+1,a+1+n);
    avg=S/n;
  
    for(int i=1;i<=n;i++)
    {
        if(a[i]<avg)
        {   
            
            a1[i]=a[i];
            S-=a[i];
            avg=S/(n-i);  
        }
        else
        {
            a1[i]=avg;
        }

    }
    
        double avg1=0;
        double fang=0;
        for(int i=1;i<=n;i++)
        avg1+=a1[i];
        avg1/=n;
        for(int i=1;i<=n;i++)
        fang+=pow((a1[i]-avg1),2);
        fang=sqrt(fang/n);
        printf("%.4lf",fang);
    

    system("pause");
    return 0;
}

8.迷宫(标记dfs)

分别测试这100个点即可，每次测试后要情况要把数据清空。这题本来不想记的，UDLR的时候我判断错了，i是行坐标判断上下而且U应该是-1，没想到自己会错在这个地方

#include

using namespace std;
char ma[50][50];
bool vis[50][50];
int n=10;
int ans=0;
void solve(int i,int j){
    if(i<=0||j<=0||i>n||j>n)
    {
        ans++;
        return;
    }
    if(vis[i][j]==true)return ;
    vis[i][j]=true;
    switch (ma[i][j])
    {
    case 'L':solve(i,j-1);
        break;
    case 'R':solve(i,j+1);
        break; 
    case 'U':solve(i-1,j);
        break;
    case 'D':solve(i+1,j);
        break;
    
    default:
        break;
    }
}
int main(){
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    cin>>ma[i][j];
    
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    {
        memset(vis,0,sizeof(vis));
        solve(i,j);

    }
    cout<<ans<<endl;
    system("pause");
    return 0;
}

9.跳蚱蜢（bfs+set判重）

这题判断最小步数我居然没想到bfs，判断最优解一定是BFS!!第一次用set集合来判重，然后判断的时候犯了一个大忌，直接把出队的节点进行修改，正确做法应该是赋值给另外一个节点再做操作。

#include
using namespace std;
int dis[]={-1,-2,1,2};
struct node{
    string str;
    int pos;
    int depth;  
    node(string str1,int pos1,int depth1){
        str=str1;//以后还是这样写，不要同名，大忌！
        pos=pos1;
        depth=depth1;
    }
};
string start="012345678";
string e="087654321";
int pos1;
int main(){
    struct node node1(start,0,0);
    struct node node2("",0,0);
    queue<struct node> que;
    set<string >s;//判重
    que.push(node1); 
    s.insert(node1.str);//记得第一个节点先放入集合
    while(!que.empty()){
      node2=que.front();
      que.pop();
      if(node2.str==e)//跳出情况
      {
          cout<<node2.depth<<endl;
          break;
      }  
      for(int i=0;i<4;i++)
      {             
          node temp("",0,0); //之前直接用node2进行修改，大忌！
          temp=node2;
          pos1=node2.pos+dis[i]+9;
          pos1%=9;
          swap(temp.str[node2.pos],temp.str[pos1]);//直接用swap函数
          temp.pos=pos1;
          temp.depth++;
          if(s.count(temp.str)==0)
          {//可能会跳出跟以前重复的情况，count函数为0表示没有
          que.push(temp);
          s.insert(temp.str);
          }
      }

    }

    system("pause");
    return 0;
}

9.方格分割

从中间左边（3，3）开始往两边同时dfs，然后遇到边就结束，ans++。可以验证，图中有4个方向dfs导致的结果是一样的，所以最后ans/=4.
这题我一开始认为要走到底角才结束，判定走到一个角才停止dfs。属实白痴，这样算出来的会多多于结果，因为相同的图案可能有多种走到同一个角的方式。

#include
using namespace std;
int vis[10][10];
int ans=0;
int dir[4][2]={0,1,0,-1,1,0,-1,0};
void dfs(int i,int j){
    
    if((i==0||j==6||i==6||j==0)){
        ans++;
        return;
    }
  

    for(int k=0;k<4;k++)
    {   
        int o=i+dir[k][0];
        int p=j+dir[k][1];
        if(!vis[o][p]&&o>=0&&o<7&&p>=0&&p<7)
        {
            vis[o][p]=vis[6-o][6-p]=1;
            dfs(o,p);
            vis[o][p]=vis[6-o][6-p]=0;
        }
    }
}
int main(){
    vis[3][3]=1;
    dfs(3,3);
    cout<<ans;

    system("pause");
    return 0;
}

10.方格问题（递归）

遇到左括号就一层dfs，并把结果返回给当前的记录值，遇到或和右括号就判断当前最大值。最后while循环结束时候不能忘记再算一遍最大值。

#include
using namespace std;
string str;
int k=0;
int dfs(){
	int cnt=0;//表示当前的x，包括括号内的
	int m=0;
	while(k<str.size()){
		if(str[k]=='('){
			k++;
			cnt+=dfs();
		}else if(str[k]=='x'){
			k++;
			cnt++;
		}else if(str[k]=='|'){
			k++;
			m=max(m,cnt);
			cnt=0;
		}else if(str[k]==')'){
			k++;
			m=max(m,cnt);
			return m;
		}
	}
		m=max(m,cnt);
		return m;
}

int main(){
	cin>>str;	
	cout<<dfs();
	system("pause");
	return 0;
}

11.包子凑数

首先如果公约数不为1，直接INF。否则，进行递推，对每个点都加上数组里边的数进行标记，标记到了就是可访问的。若a，b互素，ax+by=c，若x，y>0，无解的C中最大取a*b-a-b，所以这里数组开1w。然后为了在遍历中防止越界还要记得加限定条件。

#include
using namespace std;
int gcd(int a,int b){
	return b?gcd(b,a%b):a;
}
int f[10001];//直接100*100,不是很懂这个
int a[101];
int main(){
	int n;
	cin>>n;
	int g=0;
	for(int i=1;i<=n;i++)
	{	
		cin>>a[i];
		if(i==1)g=a[i];
		g=gcd(g,a[i]);
	}
	if(g!=1){
		cout<<"INF"<<endl;
	}
	else{
		int ans=0;
		f[0]=1;
		for(int i=1;i<=n;i++)
		{
			for(int j=0;a[i]+j<=10000;j++)
			if(f[j])f[j+a[i]]=1;
		}
		
		for(int i=1;i<=10000;i++)
		if(!f[i])ans++;
		cout<<ans<<endl;
	}


	system("pause");
	return 0;
}

12.分巧克力（二分）

涉及到整数的二分，为了避免死循环，可以使用该模板
while l mid=(l+r+1)/2//当l和r差1的时候 mid会变成r
if l=mid
else r=mid-1

#include
using namespace std;
int N,K;
int h[100001];
int w[100001];
bool f(int x){
	int cnt=0;
	for(int i=1;i<=N;i++)//=没加调了半天
	cnt+=(h[i]/x)*(w[i]/x);//括号没加出大事！
	if(cnt>=K)return true;
	
	 return false;
}
//要找的是符合条件的最右端
int main(){
	cin>>N>>K;
	for(int i=1;i<=N;i++)
	cin>>h[i]>>w[i];
	int r=100000;
	int l=0;
	int mid;
	while(l<r){  
		mid=(r+l+1)>>1;// 20 21 20 且l可能l=mid导致死循环，所以加1让mid大于左边


		//如果mid满足条件，说明从mid往右有最优解，所以l=mid
		if(f(mid))l=mid;//边长增加，块减少
		else r=mid-1;
		//现在是 20 21 21 ，这里如果不-1会死循环，和上面原理一样
		//所以这里把上面导到这里，然后-1做一个出口
	}
	cout<<l<<endl;
	system("pause");
	return 0;
}

下面这种方式也行，思路不一样
首先r-l>1已经避免死循环，其次，r=mid的情况仅当mid非正解，所以r永远不能取。反观l，l仅当mid为解才能取，while结束之后，l的值就是答案，而r的值不是答案。

	while(r-l>1){  
		mid=(r+l)>>1;
		if(f(mid))l=mid;
		else r=mid;
	}

13.方格填数(暴力+next_permutation)

#include
using namespace std;
int a[10];
int ans=0;
void func(){
	if(abs(a[0]-a[1])==1)return ;
	if(abs(a[0]-a[3])==1)return ;
	if(abs(a[0]-a[4])==1)return ;
	if(abs(a[0]-a[5])==1)return ;
	if(abs(a[2]-a[1])==1)return ;
	if(abs(a[4]-a[1])==1)return ;
	if(abs(a[5]-a[1])==1)return ;
	if(abs(a[6]-a[1])==1)return ;
	if(abs(a[6]-a[2])==1)return ;
	if(abs(a[5]-a[2])==1)return ;
	if(abs(a[3]-a[4])==1)return ;
	if(abs(a[3]-a[7])==1)return ;
	if(abs(a[3]-a[8])==1)return ;
	if(abs(a[4]-a[5])==1)return ;
	if(abs(a[4]-a[7])==1)return ;
	if(abs(a[4]-a[8])==1)return ;
	if(abs(a[4]-a[9])==1)return ;
	if(abs(a[5]-a[6])==1)return ;
	if(abs(a[5]-a[8])==1)return ;
	if(abs(a[5]-a[9])==1)return ;
	if(abs(a[6]-a[9])==1)return ;
	if(abs(a[7]-a[8])==1)return ;
	if(abs(a[8]-a[9])==1)return ;

	ans++;
	return ;
}
int main(){
	for(int i=0;i<10;i++)
		a[i]=i;
	do{
		func();
	}while(next_permutation(a,a+10));
	cout<<ans++<<endl;
	system("pause");
	return 0;
}

14.寒假作业

用全排列会T。转而用dfs，过程中要注意两点，一点是剪枝的时候要加上step判定，另外就是结尾的除法转换成乘法，除法太容易错！

#include
using namespace std;
int a[14];
int vis[14];
int ans=0;
void dfs(int step){
  if(a[1]+a[2]!=a[3]&&step>3)return;
  if(a[4]-a[5]!=a[6]&&step>6)return;
  if(a[7]*a[8]!=a[9]&&step>9)return;
  if(a[12]*a[11]==a[10]&&step>12){
	  ans++;
	  return ;
  }
  
  for(int i=1;i<=13;i++)
  {
	  if(!vis[i])
	  {
		  vis[i]=1;
		  a[step]=i;
		  dfs(step+1);
		  vis[i]=0;
	  }
  }
}

int main(){
	dfs(1);
	cout<<ans<<endl;
	system("pause");
	return 0;
}

15.剪邮票（双重dfs）

思路是先用dfs求出组合数，然后把组合数映射到二维数组里求连通分量个数。卡了很久的一道题，值得一刷。我在solve里面的双重for循环用了break退出导致错误，应该用return。
而且貌似求连通分量个数的dfs跟一般的dfs不一样，前者不需要还原状态，只需要进行清除标记即可。

#include
using namespace std;
int f[6];
int vis[13];
int cnt;
int ans=0;
int g[4][5];
int dir[][2]={-1,0,1,0,0,1,0,-1};

void solve(int x,int y){
    if(x<1||y<1||x>3||y>4)return ;
    if(cnt==5){
        ans++;
        for(int i=1;i<=5;i++)
        cout<<f[i]<<" ";
        cout<<endl;
        return ;

    }
    int x1,y1;
    for(int k=0;k<4;k++){
        x1=x+dir[k][0];
        y1=y+dir[k][1];
        if(g[x1][y1]){
            cnt++;
            g[x1][y1]=0;
            solve(x1,y1);
        } 
    }
}
void check(){
    memset(g,0,sizeof(g));
    cnt=0;
    for(int i=1;i<=5;i++){//填入二维数组
        int x=f[i];
        if(x%4!=0) g[x/4+1][x%4]=1;
        else g[x/4][4]=1;
    }

    for(int i=1;i<=3;i++)
    for(int j=1;j<=4;j++)
    if(g[i][j]){
        cnt++;
        g[i][j]=0;//避免重复搜索
        solve(i,j);
        return ;//因为是判断联通，找一个点搜就行
        //这里不需要状态还原了
    }
}

void dfs(int step){
    if(step==6){
        check();
        return;
    }
    for(int i=1;i<=12;i++)
    {
        if(!vis[i]&&i>f[step-1]){
            vis[i]=1;
            f[step]=i;
            dfs(step+1);
            vis[i]=0;
        }
    }
 
}


int main(){
    dfs(1);
    cout<<ans<<endl;
    system("pause");
    return 0;
}

16.四平方和

思路:一开始就是枚举，4层for循环，然后可以用n/4，n/2等等优化，没什么用，铁T。随后可以用三层for循环，最后一层进行计算，还是T。最后用的是哈希的思想，把c，d的平方和存起来，然后用map的find函数找，优化很多，但是由于find函数是on，所以还是t。最后把map改成数组就能过了！

#include
using namespace std;
int n;
int has[10000000];
int main(){
    cin>>n;
    int c,d;
    for(int i=0;i*i<=n/2;i++)//构造哈希
    for(int j=i;j*j+i*i<=n;j++)
    if(has[i*i+j*j]==0) //只记录一次 这样可以保证相同的和字典序最小
    has[i*i+j*j]=i+1;//防止i为0的情况
    for(int i=0;i*i<=n/4;i++)   
    for(int j=i;i*i+j*j<=n/2;j++){
        if(has[n-i*i-j*j]){
            c=has[n-i*i-j*j]-1;
            d=sqrt(n-i*i-j*j-c*c);
            printf("%d %d %d %d\n",i,j,c,d);
            system("pause");
            return 0;
        }
    }
    system("pause");
    return 0;
}