机器学习:Logistic回归(Python)
Logistic回归(二分类)
logistic_regression_class2.py
import numpy as np
import matplotlib.pyplot as plt
class LogisticRegression:
"""
逻辑回归,采用梯度下降算法 + 正则化,交叉熵损失函数,实现二分类
"""
def __init__(self, fit_intercept=True, normalize=True, alpha=0.05, eps=1e-10,
max_epochs=300, batch_size=20, l1_ratio=None, l2_ratio=None, en_rou=None):
"""
:param eps: 提前停止训练的精度要求,按照两次训练损失的绝对值差小于eps,停止训练
:param fit_intercept: 是否训练偏置项
:param normalize: 是否标准化
:param alpha: 学习率
:param max_epochs: 最大迭代次数
:param batch_size: 批量大小,若为1,则为随机梯度,若为训练集样本量,则为批量梯度,否则为小批量梯度
:param l1_ratio: LASSO回归惩罚项系数
:param l2_ratio: 岭回归惩罚项系数
:param en_rou: 弹性网络权衡L1和L2的系数
"""
self.fit_intercept = fit_intercept # 线性模型的常数项。也即偏置bias,模型中的theta0
self.normalize = normalize # 是否标准化数据
self.alpha = alpha # 学习率
self.eps = eps # 提前停止训练
if l1_ratio:
if l1_ratio < 0:
raise ValueError("惩罚项系数不能为负数")
self.l1_ratio = l1_ratio # LASSO回归惩罚项系数
if l2_ratio:
if l2_ratio < 0:
raise ValueError("惩罚项系数不能为负数")
self.l2_ratio = l2_ratio # 岭回归惩罚项系数
if en_rou:
if en_rou > 1 or en_rou < 0:
raise ValueError("弹性网络权衡系数范围在[0, 1]")
self.en_rou = en_rou # 弹性网络权衡L1和L2的系数
self.max_epochs = max_epochs
self.batch_size = batch_size
self.theta = None # 训练权重系数
if normalize:
self.feature_mean, self.feature_std = None, None # 特征的均值,标准方差
self.n_samples, self.n_features = 0, 0 # 样本量和特征数
self.train_loss, self.test_loss = [], [] # 存储训练过程中的训练损失和测试损失
def init_theta_params(self, n_features):
"""
初始化参数
如果训练偏置项,也包含了bias的初始化
:return:
"""
self.theta = np.random.randn(n_features, 1) * 0.1
@staticmethod
def sigmoid(x):
"""
sigmoid函数,为避免上溢或下溢,对参数x做限制
:param x: 可能是标量数据,也可能是数组
:return:
"""
x = np.asarray(x) # 为避免标量值的布尔索引出错,转换为数组
x[x > 30.0] = 30.0 # 避免下溢
x[x < -50] = -50.0 # 避免上溢
return 1 / (1 + np.exp(-x))
@staticmethod
def sign_func(weight):
"""
符号函数,针对L1正则化
:param weight: 模型系数
:return:
"""
sign_values = np.zeros(weight.shape)
sign_values[np.argwhere(weight > 0)] = 1 # np.argwhere(weight > 0) 返回值是索引下标
sign_values[np.argwhere(weight < 0)] = -1
return sign_values
@staticmethod
def cal_cross_entropy(y_test, y_prob):
"""
计算交叉熵损失
:param y_test: 样本真值
:param y_prob: 模型预测类别概率
:return:
"""
loss = -(y_test.T.dot(np.log(y_prob)) + (1 - y_test).T.dot(np.log(1 - y_prob)))
return loss
def fit(self, x_train, y_train, x_test=None, y_test=None):
"""
样本的预处理,模型系数的求解,闭式解公式 + 梯度方法
:param x_train: 训练样本集 m*k
:param y_train: 训练目标集 m*1
:param x_test: 测试样本集 n*k
:param y_test: 测试目标集 n*1
:return:
"""
if self.normalize:
self.feature_mean = np.mean(x_train, axis=0) # 样本均值
self.feature_std = np.std(x_train, axis=0) + 1e-8 # 样本方差
x_train = (x_train - self.feature_mean) / self.feature_std # 标准化
if x_test is not None:
x_test = (x_test - self.feature_mean) / self.feature_std # 标准化
if self.fit_intercept:
x_train = np.c_[x_train, np.ones_like(y_train)] # 添加一列1,即偏置项样本
if x_test is not None and y_test is not None:
x_test = np.c_[x_test, np.ones_like(y_test)] # 添加一列1,即偏置项样本
self.init_theta_params(x_train.shape[1]) # 初始化参数
# 训练模型
self._fit_gradient_desc(x_train, y_train, x_test, y_test) # 梯度下降法训练模型
def _fit_gradient_desc(self, x_train, y_train, x_test=None, y_test=None):
"""
三种梯度下降求解 + 正则化:
(1)如果batch_size为1,则为随机梯度下降法
(2)如果batch_size为样本量,则为批量梯度下降法
(3)如果batch_size小于样本量,则为小批量梯度下降法
:return:
"""
train_sample = np.c_[x_train, y_train] # 组合训练集和目标集,以便随机打乱样本
# np.c_水平方向连接数组,np.r_竖直方向连接数组
# 按batch_size更新theta,三种梯度下降法取决于batch_size的大小
best_theta, best_mse = None, np.infty # 最佳训练权重与验证均方误差
for epoch in range(self.max_epochs):
self.alpha *= 0.95
np.random.shuffle(train_sample) # 打乱样本顺序,模拟随机化
batch_nums = train_sample.shape[0] // self.batch_size # 批次
for idx in range(batch_nums):
# 取小批量样本,可以是随机梯度(1),批量梯度(n)或者是小批量梯度( n * k = 1 * k --> 转置 k * 1
delta = ((y_prob_batch - batch_y).T.dot(batch_x) / self.batch_size).T
# 计算并添加正则化部分,不包含偏置项
dw_reg = np.zeros(shape=(x_train.shape[1] - 1, 1))
if self.l1_ratio and self.l2_ratio is None:
# LASSO回归,L1正则化
dw_reg = self.l1_ratio * self.sign_func(self.theta[:-1])
if self.l2_ratio and self.l1_ratio is None:
# Ridge回归,L2正则化
dw_reg = 2 * self.l2_ratio * self.theta[:-1]
if self.en_rou and self.l1_ratio and self.l2_ratio:
# 弹性网络
dw_reg = self.l1_ratio * self.en_rou * self.sign_func(self.theta[:-1])
dw_reg += 2 * self.l2_ratio * (1 - self.en_rou) * self.theta[:-1]
delta[:-1] += dw_reg / self.batch_size # 添加了正则化
self.theta = self.theta - self.alpha * delta
# 计算训练过程中的交叉熵损失值
y_train_prob = self.sigmoid(x_train.dot(self.theta)) # 当前迭代训练的模型预测概率
train_cost = self.cal_cross_entropy(y_train, y_train_prob) # 训练集的交叉熵损失
self.train_loss.append(train_cost / x_train.shape[0]) # 交叉熵损失均值
if x_test is not None and y_test is not None:
y_test_prob = self.sigmoid(x_test.dot(self.theta)) # 当前测试样本预测概率
test_cost = self.cal_cross_entropy(y_test, y_test_prob)
self.test_loss.append(test_cost / x_test.shape[0]) # 交叉熵损失均值
# 两次交叉熵损失均值的差异小于给定的均值,提前停止训练
if epoch > 10 and (np.abs(self.train_loss[-1] - self.train_loss[-2])) <= self.eps:
break
def get_params(self):
"""
返回线性模型训练的系数
:return:
"""
if self.fit_intercept: # 存在偏置项
weight, bias = self.theta[:-1], self.theta[-1]
else:
weight, bias = self.theta, np.array([0])
if self.normalize: # 标准化后的系数
weight = weight / self.feature_std.reshape(-1, 1) # 还原模型系数
bias = bias - weight.T.dot(self.feature_mean)
return weight.reshape(-1), bias
def predict_prob(self, x_test):
"""
预测测试样本的概率,第1列为y = 0的概率,第2列是y = 1的概率
:param x_test: 测试样本,ndarray:n * k
:return:
"""
y_prob = np.zeros((x_test.shape[0], 2)) # 预测概率
if self.normalize:
x_test = (x_test - self.feature_mean) / self.feature_std # 测试数据标准化
if self.fit_intercept:
# 存在偏置项,加一列1
x_test = np.c_[x_test, np.ones(shape=x_test.shape[0])]
y_prob[:, 1] = self.sigmoid(x_test.dot(self.theta)).reshape(-1)
y_prob[:, 0] = 1 - y_prob[:, 1] # 类别y = 0的概率
return y_prob
def predict(self, x, p=0.5):
"""
预测样本类别,默认大于0.5为1,小于0.5为0
:param x: 预测样本
:param p: 概率阈值
:return:
"""
y_prob = self.predict_prob(x)
# 布尔值转换为整数,true对应1,false对应0
return (y_prob[:, 1] > p).astype(int)
def plt_loss_curve(self, lab=None, is_show=True):
"""
可视化交叉熵损失曲线
:param is_show: 是否可视化
:return:
"""
if is_show:
plt.figure(figsize=(8, 6))
plt.plot(self.train_loss, "k-", lw=1, label="Train Loss")
if self.test_loss:
plt.plot(self.test_loss, "r--", lw=1.2, label="Test Loss")
plt.xlabel("Training Epochs", fontdict={"fontsize": 12})
plt.ylabel("The Mean of Cross Entropy Loss", fontdict={"fontsize": 12})
plt.title("%s: The Loss Curve of Cross Entropy" % lab)
plt.legend(frameon=False)
plt.grid(ls=":")
# plt.axis([0, 300, 20, 30])
if is_show:
plt.show()
performance_metrics.py
import numpy as np # 数值计算
import pandas as pd # 数值分析
import matplotlib.pyplot as plt # 可视化
import seaborn as sns
class ModelPerformanceMetrics:
"""
模型性能度量,分二分类和多分类,模型的泛化性能度量
1. 计算混淆矩阵
2. 计算分类报告,模板采用sklearn.classification_report格式
3. 计算P(查准率)R(查全率)指标,并可视化P—R曲线,计算AP
4. 计算ROC的指标:真正例率,假正例率,并可视化ROC曲线,计算AUC
5. 计算代价曲线,归一化指标、正例概率代价、可视化代价曲线,并计算期望总体代价
"""
def __init__(self, y_true, y_prob):
"""
初始化参数
:param y_true: 样本的真实类别
:param y_prob: 样本的预测类别概率
"""
self.y_true = np.asarray(y_true, dtype=np.int64)
self.y_prob = np.asarray(y_prob, np.float64) # 列数与类别数一致
self.n_samples, self.n_class = self.y_prob.shape # 样本量和类别数
if self.n_class > 2:
self.y_true = self.label_one_hot()
else:
self.y_true = self.y_true.reshape(-1)
self.cm = self.cal_confusion_matrix() # 计算混淆矩阵
def label_one_hot(self):
"""
对真实类别标签进行one—hot编码,编码后的维度与模型预测概率维度一致
:return: y_true_lab
"""
y_true_lab = np.zeros((self.n_samples, self.n_class))
for i in range(self.n_samples):
y_true_lab[i, self.y_true[i]] = 1
return y_true_lab
def cal_confusion_matrix(self):
"""
计算并构建混淆矩阵
:return: confusion_matrix
"""
confusion_matrix = np.zeros((self.n_class, self.n_class), dtype=np.int64)
for i in range(self.n_samples):
idx = np.argmax(self.y_prob[i, :]) # 最大概率所对应的索引,即是类别
if self.n_class == 2:
idx_true = self.y_true[i] # 第i个样本的真实类别
else:
idx_true = np.argmax(self.y_true[i, :])
if idx_true == idx:
confusion_matrix[idx, idx] += 1 # 预测正确,则在对角线位置加1
else:
confusion_matrix[idx_true, idx] += 1 # 预测错误,则在真实类别行,预测错误列加1
return confusion_matrix
def cal_classification_report(self, target_names=None):
"""
计算并构造分类报告
:param self:
:return:
"""
precision = np.diag(self.cm) / np.sum(self.cm, axis=0) # 查准率
recall = np.diag(self.cm) / np.sum(self.cm, axis=1) # 查全率
f1_score = 2 * precision * recall / (precision + recall) # F1调和平均
support = np.sum(self.cm, axis=1, dtype=np) # 各个类别的支持样本量
support_all = np.sum(support) # 总的样本量
accuracy = np.sum(np.diag(self.cm)) / support_all # 准确率
p_m, r_m = precision.mean(), recall.mean()
macro_avg = [p_m, r_m, 2 * p_m * r_m / (p_m + r_m)] # 宏指标
weight = support / support_all # 以各个类别的样本量所占总的样本量比例为权重
weighted_avg = [np.sum(weight * precision), np.sum(weight * recall), np.sum(weight * f1_score)]
# 构造分类报告
metrics_1 = pd.DataFrame(np.array([precision, recall, f1_score, support]).T,
columns=["precision", "recall", "f1_score", "support"])
metrics_2 = pd.DataFrame([["", "", "", ""], ["", "", accuracy, support_all],
np.hstack([macro_avg, support_all]),
np.hstack([weighted_avg, support_all])],
columns=["precision", "recall", "f1_score", "support"])
c_report = pd.concat([metrics_1, metrics_2], ignore_index=False)
if target_names is None: # 类别标签未传参,则默认类别标签为0、1、2...
target_names = [str(i) for i in range(self.n_class)]
else:
target_names = list(target_names)
target_names.extend(["", "accuracy", "macro_avg", "weighted_avg"])
c_report.index = target_names
return c_report
@staticmethod
def __sort_positive__(y_prob):
"""
按照预测为正例的概率进行降序排列,并返回排序的索引向量
:param y_prob: 一维数组,样本预测为正例的概率
:return:
"""
idx = np.argsort(y_prob)[::-1] # 降序排列
return idx
def precision_recall_curve(self):
"""
Precision和Recall曲线,计算各坐标点的值,可视化P—R曲线
:return:
"""
pr_array = np.zeros((self.n_samples, 2)) # 存储每个样本预测概率作为阈值时的P和R指标
if self.n_class == 2: # 二分类
idx = self.__sort_positive__(self.y_prob[:, 0]) # 降序排列索引
y_true = self.y_true[idx] # 真值类别标签按照排序索引进行排序
# 针对每个样本,把预测概率作为阈值,计算各指标
for i in range(self.n_samples):
tp, fn, tn, fp = self.__cal_sub_metrics__(y_true, i + 1)
pr_array[i, :] = tp / (tp + fn), tp / (tp + fp)
else:
precision = np.zeros((self.n_samples, self.n_class)) # 查准率
recall = np.zeros((self.n_samples, self.n_class)) # 查全率
for k in range(self.n_class): # 针对每个类别,分别计算P、R指标,然后平均
idx = self.__sort_positive__(self.y_prob[:, k])
y_true_k = self.y_true[:, k] # 真值类别第k列
y_true = y_true_k[idx] # 对第k个类别的真值排序
# 针对每个样本,把预测概率作为阈值,计算各指标
for i in range(self.n_samples):
tp, fn, tn, fp = self.__cal_sub_metrics__(y_true, i + 1)
precision[i, k] = tp / (tp + fp) # 查准率
recall[i, k] = tp / (tp + fn) # 查全率
pr_array = np.array([np.mean(recall, axis=1), np.mean(precision, axis=1)]).T
return pr_array
def roc_metrics_curve(self):
"""
ROC曲线,计算真正例率和假正例率,并可视化
:return:
"""
roc_array = np.zeros((self.n_samples, 2)) # 存储每个样本预测概率作为阈值时的TPR和FPR指标
if self.n_class == 2: # 二分类
idx = self.__sort_positive__(self.y_prob[:, 0]) # 降序排列索引
y_true = self.y_true[idx] # 真值类别标签按照排序索引进行排序
# 针对每个样本,把预测概率作为阈值,计算各指标
n_nums, p_nums = len(y_true[y_true == 1]), len(y_true[y_true == 0]) # 真实类别中反例与正例的样本量
tp, fn, tn, fp = self.__cal_sub_metrics__(y_true, 1)
roc_array[0, :] = fp / (tn + fp), tp / (tp + fn)
for i in range(1, self.n_samples):
#tp, fn, tn, fp = self.__cal_sub_metrics__(y_true, i + 1)
if y_true[i] == 1:
roc_array[i, :] = roc_array[i - 1, 0] + 1 / n_nums, roc_array[i - 1, 1]
else:
roc_array[i, :] = roc_array[i - 1, 0], roc_array[i - 1, 1] + 1 / p_nums
#roc_array[i, :] = fp / (tn + fp), tp / (tp + fn)
else: # 多分类
precision = np.zeros((self.n_samples, self.n_class)) # 查准率
recall = np.zeros((self.n_samples, self.n_class)) # 查全率
for k in range(self.n_class): # 针对每个类别,分别计算P、R指标,然后平均
idx = self.__sort_positive__(self.y_prob[:, k])
y_true_k = self.y_true[:, k] # 真值类别第k列
y_true = y_true_k[idx] # 对第k个类别的真值排序
# 针对每个样本,把预测概率作为阈值,计算各指标
for i in range(self.n_samples):
tp, fn, tn, fp = self.__cal_sub_metrics__(y_true, i + 1)
precision[i, k] = tp / (tp + fp) # 查准率
recall[i, k] = tp / (tp + fn) # 查全率
roc_array = np.array([np.mean(recall, axis=1), np.mean(precision, axis=1)]).T
return roc_array
def __cal_sub_metrics__(self, y_true_sort, n):
"""
计算TP、TN、FP、TN
:param y_true_sort: 排序后的真实类别
:param n: 以第n个样本预测概率为阈值
:return:
"""
if self.n_class == 2:
pre_label = np.r_[np.zeros(n, dtype=np.int64), np.ones(self.n_samples - n, dtype=np.int64)]
tp = len(pre_label[(pre_label == 0) & (pre_label == y_true_sort)]) # 真正例
tn = len(pre_label[(pre_label == 1) & (pre_label == y_true_sort)]) # 真反例
fp = np.sum(y_true_sort) - tn # 假正例
fn = self.n_samples - tp - tn - fp # 假反例
else:
pre_label = np.r_[np.ones(n, dtype=np.int64), np.zeros(self.n_samples - n, dtype=np.int64)]
tp = len(pre_label[(pre_label == 1) & (pre_label == y_true_sort)]) # 真正例
tn = len(pre_label[(pre_label == 0) & (pre_label == y_true_sort)]) # 真反例
fn = np.sum(y_true_sort) - tp # 假正例
fp = self.n_samples - tp - tn - fn # 假反例
return tp, fn, tn, fp
@staticmethod
def __cal_ap__(pr_val):
"""
计算AP
:param pr_val: PR指标各坐标点的数组
:return:
"""
return (pr_val[1:, 0] - pr_val[0:-1, 0]).dot(pr_val[1:, 1])
@staticmethod
def __cal_auc__(roc_val):
"""
计算ROC曲线下的面积,即AUC
:param roc_val:
:return:
"""
return (roc_val[1:, 0] - roc_val[0:-1, 0]).dot(roc_val[:-1, 1] + roc_val[1:, 1]) / 2
def plt_pr_curve(self, pr_val, label=None, is_show=True):
"""
可视化PR曲线
:param pr_val: PR指标各坐标点的数组
:return:
"""
ap = self.__cal_ap__(pr_val)
if is_show:
plt.figure(figsize=(7, 5))
if label:
plt.step(pr_val[:, 0], pr_val[:, 1], "-", lw=2, where="post",
label = label + ", AP = %.3f" % ap)
else:
plt.step(pr_val[:, 0], pr_val[:, 1], "-", lw=2, where="post")
plt.title("Precision Recall Curve of Test Samples and AP = %.3f" % ap)
plt.xlabel("Recall", fontdict={"fontsize": 12})
plt.ylabel("Precision", fontdict={"fontsize": 12})
plt.grid(ls=":")
plt.legend(frameon=False)
if is_show:
plt.show()
def plt_roc_curve(self, roc_val, label=None, is_show=True):
"""
可视化ROC曲线
:param roc_val: ROC指标各坐标点的数组
:return:
"""
auc = self.__cal_auc__(roc_val)
if is_show:
plt.figure(figsize=(7, 5))
if label:
plt.step(roc_val[:, 0], roc_val[:, 1], "-", lw=2, where="post",
label = label + ", AP = %.3f" % auc)
else:
plt.step(roc_val[:, 0], roc_val[:, 1], "-", lw=2, where="post")
plt.title("ROC Curve of Test Samples and AUC = %.3f" % auc)
plt.xlabel("False Positive Rate", fontdict={"fontsize": 12})
plt.ylabel("True Positive Rate", fontdict={"fontsize": 12})
plt.grid(ls=":")
plt.legend(frameon=False)
if is_show:
plt.show()
@staticmethod
def plt_confusion_matrix(confusion_matrix, label_names=None, is_show=True):
"""
可视化混淆矩阵
:param confusion_matrix: 混淆矩阵
:return:
"""
sns.set()
cm = pd.DataFrame(confusion_matrix, columns=label_names, index=label_names)
sns.heatmap(cm, annot=True, cbar=False)
acc = np.diag(confusion_matrix).sum() / confusion_matrix.sum()
plt.title("Confusion Matrix and ACC = %.5f" % acc)
plt.xlabel("Predict", fontdict={"fontsize": 12})
plt.ylabel("True", fontdict={"fontsize": 12})
if is_show:
plt.show()
test_logistic_reg_2.py
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from logistic_regression_2class import LogisticRegression
import matplotlib.pyplot as plt
from performance_metrics import ModelPerformanceMetrics
bc_data = load_breast_cancer() # 加载数据集
X, y = bc_data.data, bc_data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
lg_lr = LogisticRegression(alpha=0.5, l1_ratio=0.5, batch_size=20, max_epochs=1000, eps=1e-15)
lg_lr.fit(X_train, y_train, X_test, y_test)
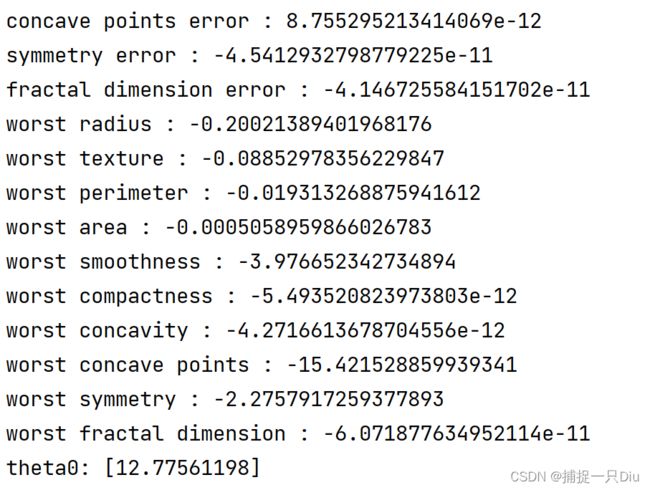
print("L1正则化模型参数如下:")
theta = lg_lr.get_params()
fn = bc_data.feature_names
for i, w in enumerate(theta[0]):
print(fn[i], ":", w)
print("theta0:", theta[1])
print("=" * 70)
y_test_prob = lg_lr.predict_prob(X_test) # 预测概率
y_test_labels = lg_lr.predict(X_test)
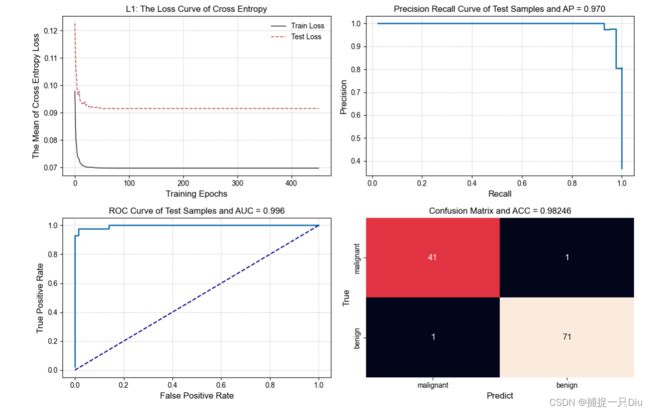
plt.figure(figsize=(12, 8))
plt.subplot(221)
lg_lr.plt_loss_curve(lab="L1", is_show=False)
pm = ModelPerformanceMetrics(y_test, y_test_prob)
print(pm.cal_classification_report())
pr_values = pm.precision_recall_curve() # PR指标值
plt.subplot(222)
pm.plt_pr_curve(pr_values, is_show=False) # PR曲线
roc_values = pm.roc_metrics_curve() # ROC指标值
plt.subplot(223)
pm.plt_roc_curve(roc_values, is_show=False) # ROC曲线
plt.subplot(224)
cm = pm.cal_confusion_matrix()
pm.plt_confusion_matrix(cm, label_names=["malignant", "benign"], is_show=False)
plt.tight_layout()
plt.show()
输出结果: