瑞486
瑞486

瑞_数据结构与算法_二叉搜索树

文章目录

    • 1 什么是二叉搜索树
      • 1.1 二叉搜索树的特征
      • 1.2 前驱后继
    • 2 二叉搜索树的Java实现
      • 2.1 定义二叉搜索树节点类BSTNode
        • 泛型key改进
      • 2.2 实现查找方法get(int key)
        • 递归实现
        • 非递归实现 ★
        • 非递归实现 泛型key版本
      • 2.3 实现查找最小方法min()
        • 递归实现
        • 非递归实现 ★
      • 2.4 实现查找最大方法max()
        • 递归实现
        • 非递归实现 ★
      • 2.5 实现新增方法put(int key, Object value)
        • 递归实现
        • 非递归实现 ★
      • 2.6 实现查找关键字的前任值predecessor(int key)
      • 2.7 查找关键字的后任值successor(int key)
      • 2.8 根据关键字删除remove(int key)
        • 非递归实现 ★
        • 递归实现
    • 3 二叉搜索树——范围查询
      • 3.1 找所有小于索引的值less(int key)
      • 3.2 找所有大于索引的值greater(int key)
      • 3.3 找范围值between(int key1, int key2)
      • 3.3 小结

前言：本文章为瑞_系列专栏之《数据结构与算法》的二叉搜索树篇。由于博主是从B站黑马程序员的《数据结构与算法》学习到的相关知识，所以本系列专栏主要针对该课程进行笔记总结和拓展，文中的部分原理及图解也是来源于黑马提供的资料。本文仅供大家交流、学习及研究使用，禁止用于商业用途，违者必究！

瑞_数据结构与算法_二叉搜索树_第1张图片

1 什么是二叉搜索树

  二叉搜索树最早是由Bernoulli兄弟在18世纪中提出的，但是真正推广和应用该数据结构的是1960年代的D.L. Gries。他的著作《The Science of Programming》中详细介绍了二叉搜索树的实现和应用。

  在计算机科学的发展中，二叉搜索树成为了一种非常基础的数据结构，被广泛应用在各种领域，包括搜索、排序、数据库索引等。随着计算机算力的提升和对数据结构的深入研究，二叉搜索树也不断被优化和扩展，例如AVL树、红黑树等。

1.1 二叉搜索树的特征

  二叉搜索树（也称二叉排序树）是符合下面特征的二叉树：

  1. 树节点增加 key 属性，用来比较谁大谁小，key 不可以重复
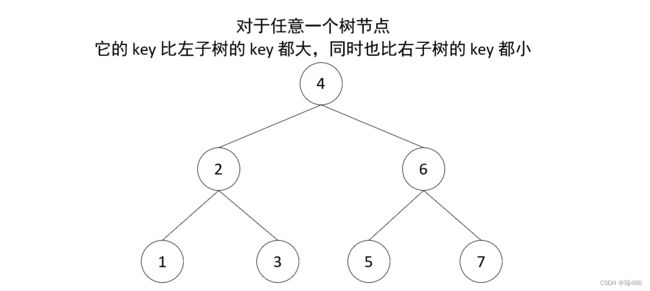
  2. 对于任意一个树节点，它的 key 比左子树的 key 都大，同时也比右子树的 key 都小，例如下图所示：

瑞_数据结构与算法_二叉搜索树_第2张图片

  轻易看出要查找 7 （从根开始）自然就可应用二分查找算法，只需三次比较

  • 与 4 比，较之大，向右找
  • 与 6 比，较之大，继续向右找
  • 与 7 比，相等，即找到

  查找的时间复杂度与树高相关，插入、删除也是如此。

  • 如果这棵树长得还不赖（左右平衡）如上图，那么时间复杂度均是 O ( log ⁡ N ) O(\log{N}) O(logN)
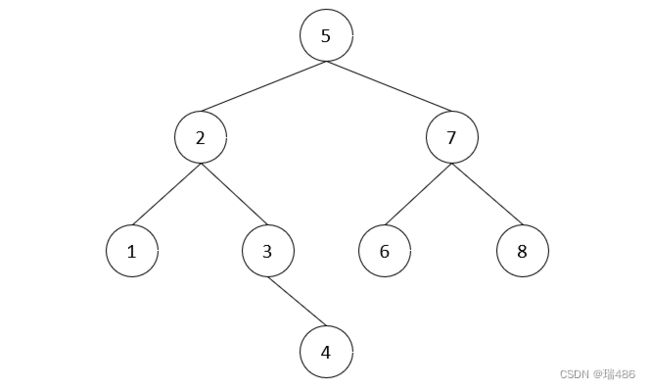
  • 当然，这棵树如果长得丑（左右高度相差过大）如下图，那么这时是最糟的情况（链表），时间复杂度是 O ( N ) O(N) O(N)

瑞_数据结构与算法_二叉搜索树_第3张图片

注：

  • 二叉搜索树 - 英文 binary search tree，简称 BST
  • 二叉排序树 - 英文 binary ordered tree 或 binary sorted tree
    二叉树的相关知识可以参考博客：《瑞_数据结构与算法_二叉树》
    二分查找的相关知识可以参考博客：瑞_数据结构与算法_二分查找

1.2 前驱后继

  • 前驱值（前任值）：找到一个离该节点最近且比该节点存储值小的值
  • 后继值（后任值）：找到一个离该节点最近且比该节点存储值大的值


2 二叉搜索树的Java实现


  以简单实现为主，主要是学习其思想，和Java中的Map集合实现的思维类似，通过key查找value

内部节点类BSTNode中含有属性：

  • 索引
  • 存储值
  • 左孩子
  • 右孩子

BSTTree二叉搜索树类含有方法：

  • 查找关键字对应的值get(int key)
  • 查找最小关键字对应值min()
  • 查找最大关键字对应值max()
  • 存储关键字和对应值put(int key, Object value)
  • 查找关键字的前任值predecessor(int key)
  • 查找关键字的后任值successor(int key)
  • 根据关键字删除remove(int key)

2.1 定义二叉搜索树节点类BSTNode

  BSTNode即二叉搜索树节点类（内部类），含有索引、存储值、左孩子、右孩子属性，由于是简单实现，索引定义基本数据类型（若希望任意类型作为 key，则后续可以将其设计为 Comparable 接口）

/**
 * Binary Search Tree 二叉搜索树
 *
 * @author LiaoYuXing-Ray
 * @version 1.0
 * @createDate 2024/1/24 19:27
 **/
public class BSTTree {
    /**
     * 根节点
     */
    BSTNode root;

    static class BSTNode {
        // 索引，比较值
        int key;
        // 该节点的存储值
        Object value;
        // 左孩子
        BSTNode left;
        // 右孩子
        BSTNode right;

        public BSTNode(int key) {
            this.key = key;
        }

        public BSTNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        public BSTNode(int key, Object value, BSTNode left, BSTNode right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }
    
    
}
泛型key改进

  使用泛型上限语法，让泛型的Key继承Comparable接口，使其能够进行大小比较。改进后代码如下（含get方法）：

/**
 * 二叉搜索树, 泛型 key 版本
 */
public class BSTTree<K extends Comparable<K>, V> {

    static class BSTNode<K, V> {
        K key;
        V value;
        BSTNode<K, V> left;
        BSTNode<K, V> right;

        public BSTNode(K key) {
            this.key = key;
        }

        public BSTNode(K key, V value) {
            this.key = key;
            this.value = value;
        }

        public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

    BSTNode<K, V> root;

    public V get(K key) {
        if (key == null) {
            return null;
        }
        BSTNode<K, V> node = root;
        while (node != null) {
            int result = key.compareTo(node.key);
            if (result < 0) {
                node = node.left;
            } else if (result > 0) {
                node = node.right;
            } else {
                return node.value;
            }
        }
        return null;
    }
}

瑞：此处泛型没有定义为T而定义K，是因为K、V迎合map集合中的key，value，容易理解

2.2 实现查找方法get(int key)

  get(int key)方法通过关键字查找对应的值

递归实现

  get(int key)方法是通过key索引关键字查找对应的值，可以使用递归查找

    /**
     * 
查找关键字对应的值

     *
     * @param key 关键字
     * @return 关键字对应的值
     */
    public Object get(int key) {
        return doGet(root, key);
    }

    /**
     * 私有 - 封装BSTNode参数，外部只需要调用get(int key)方法即可，不用关心具体细节
     *
     * @param node 根节点
     * @param key 索引关键字 
     * @return java.lang.Object 关键字对应的值
     * @author LiaoYuXing-Ray 2024/1/24 19:53
     **/
    private Object doGet(BSTNode node, int key) {
        if (node == null) {
            return null; // 没找到
        }
        if (key < node.key) {
            return doGet(node.left, key); // 向左找
        } else if (node.key < key) {
            return doGet(node.right, key); // 向右找
        } else {
            return node.value; // 找到了
        }
    }

瑞：该递归实现是尾递归

  尾递归是一种特殊形式的递归，它的特点是在函数的最后一步调用自身，并且不需要保留外层函数的调用记录。
  注意区别伪递归，伪递归通常指的是使用迭代实现的递归算法，它们在逻辑上模拟了递归的过程，但实际上并不通过函数调用自身来实现。

  尾递归的特点：

  • 在函数的最后一步调用自身，不保留外层函数的调用记录。
  • 可以仅使用常量级的栈空间，与迭代过程类似。
  • 有着与循环同样优秀的计算性能。

    伪递归的特点：
  • 使用迭代来模拟递归的逻辑。
  • 不涉及实际的函数自我调用。
  • 通常用于那些不支持尾递归优化的编程语言中，以减少内存消耗。

  方法测试代码如下：

/**
 * Binary Search Tree 二叉搜索树
 *
 * @author LiaoYuXing-Ray
 * @version 1.0
 * @createDate 2024/1/24 19:27
 **/
public class BSTTree {
    /**
     * 根节点
     */
    BSTNode root;

    static class BSTNode {
        // 索引，比较值
        int key;
        // 该节点的存储值
        Object value;
        // 左孩子
        BSTNode left;
        // 右孩子
        BSTNode right;

        public BSTNode(int key) {
            this.key = key;
        }

        public BSTNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        public BSTNode(int key, Object value, BSTNode left, BSTNode right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

    /**
     * 
查找关键字对应的值

     * 递归实现
     *
     * @param key 关键字
     * @return 关键字对应的值
     */
    public Object get(int key) {
        return doGet(root, key);
    }

    /**
     * 私有 - 封装BSTNode参数，外部只需要调用get(int key)方法即可，不用关心具体细节
     *
     * @param node 根节点
     * @param key  索引关键字
     * @return java.lang.Object 关键字对应的值
     * @author LiaoYuXing-Ray 2024/1/24 19:53
     **/
    private Object doGet(BSTNode node, int key) {
        if (node == null) {
            return null; // 没找到
        }
        if (key < node.key) {
            return doGet(node.left, key); // 向左找
        } else if (node.key < key) {
            return doGet(node.right, key); // 向右找
        } else {
            return node.value; // 找到了
        }
    }

    public static void main(String[] args) {
        /*
                     4
                   /   \
                  2     6
                 / \   / \
                1   3 5   7
         */
        BSTNode n1 = new BSTNode(1, "Ray1");
        BSTNode n3 = new BSTNode(3, "Ray3");
        BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);

        BSTNode n5 = new BSTNode(5, "Ray5");
        BSTNode n7 = new BSTNode(7, "Ray7");
        BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);
        BSTNode root = new BSTNode(4, "Ray4", n2, n6);

        BSTTree tree = new BSTTree();
        tree.root = root;

        for (int i = 0; i <= 8; i++) {
            System.out.println(tree.get(i));
        }

    }


}

  运行结果如下，找不到索引为0和8的元素存储值，而1-7都能找到，符合预期：

    null
    Ray1
    Ray2
    Ray3
    Ray4
    Ray5
    Ray6
    Ray7
    null
非递归实现 ★

  由于之前使用的是尾递归实现，而尾递归转换成迭代法是非常容易的，性能上也能有所提升，所以一般情况下，如果使用尾递归都会转化为迭代法。

    /**
     * 
查找关键字对应的值

     * 非递归实现
     *
     * @param key 关键字
     * @return 关键字对应的值
     */
    public Object get(int key) {
        BSTNode node = root;
        while (node != null) {
            if (key < node.key) {
                // 向左找
                node = node.left;
            } else if (node.key < key) {
                // 向右找
                node = node.right;
            } else {
                // 找到
                return node.value;
            }
        }
        // 没找到
        return null;
    }

瑞：测试用例可以使用同一个，同样能通过，且性能更佳。

非递归实现 泛型key版本

  如果希望让除 int 外更多的类型能够作为 key，一种方式是 key 必须实现 Comparable 接口。

  由于compareTo方法返回-1，表示key < node.key，0表示key == node.key，1表示key > node.key，所以改进后代码如下：

    public V get(K key) {
        BSTNode<K, V> node = root;
        while (node != null) {
            /*
                -1 key < p.key
                0 key == p.key
                1 key > p.key
             */
            int result = key.compareTo(node.key);
            if (result < 0) {
                node = node.left;
            } else if (result > 0) {
                node = node.right;
            } else {
                return node.value;
            }
        }
        return null;
    }

  还有一种做法不要求 key 实现 Comparable 接口，而是在构造 Tree 时把比较规则作为 Comparator 传入，将来比较 key 大小时都调用此 Comparator 进行比较，这种做法可以参考 Java 中的 java.util.TreeMap

  方法测试代码如下：

/**
 * 二叉搜索树, 泛型 key 版本
 */
public class BSTTree<K extends Comparable<K>, V> {

    static class BSTNode<K, V> {
        K key;
        V value;
        BSTNode<K, V> left;
        BSTNode<K, V> right;

        public BSTNode(K key) {
            this.key = key;
        }

        public BSTNode(K key, V value) {
            this.key = key;
            this.value = value;
        }

        public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }

    BSTNode<K, V> root;

    public V get(K key) {
        if (key == null) {
            return null;
        }
        BSTNode<K, V> node = root;
        while (node != null) {
            /*
                -1 key < node.key
                0 key == node.key
                1 key > node.key
             */
            int result = key.compareTo(node.key);
            if (result < 0) {
                node = node.left;
            } else if (result > 0) {
                node = node.right;
            } else {
                return node.value;
            }
        }
        return null;
    }

    public static void main(String[] args) {

        BSTNode<String,String> n1 = new BSTNode<>("a", "RayA");
        BSTNode<String,String> n3 = new BSTNode<>("c", "RayC");
        BSTNode<String,String> n2 = new BSTNode<>("b", "RayB", n1, n3);

        BSTNode<String,String> n5 = new BSTNode<>("e","RayE");
        BSTNode<String,String> n7 = new BSTNode<>("g","RayG");
        BSTNode<String,String> n6 = new BSTNode<>("f", "RayF", n5, n7);
        
        BSTNode<String,String> root = new BSTNode<>("d", "RayD", n2, n6);

        BSTTree<String,String> tree = new BSTTree<>();
        tree.root = root;
        
        System.out.println(tree.get("a"));
        System.out.println(tree.get("b"));
        System.out.println(tree.get("c"));
        System.out.println(tree.get("d"));
        System.out.println(tree.get("e"));
        System.out.println(tree.get("f"));
        System.out.println(tree.get("g"));
        System.out.println(tree.get("h"));
    }
}

  运行结果如下，符合预期：

	RayA
	RayB
	RayC
	RayD
	RayE
	RayF
	RayG
	null

由于使用泛型代码阅读对新手会比较困难，本文主要是学习思想，所以后续方法采用int类型作为key

2.3 实现查找最小方法min()

  min()方法查找最小关键字key的对应存储值

递归实现

  根据二叉搜索树的特征，树中最左的节点即为最小索引（关键字），即向左走到头即可，所以只要左孩子为null，即找到最小关键字，使用递归实现的代码就非常简单，如下：

    /**
     * 
查找最小关键字对应值

     * 递归实现
     *
     * @return 关键字对应的值
     */
    public Object min() {
        return doMin(root);
    }

    public Object doMin(BSTNode node) {
        if (node == null) {
            return null;
        }
        // 左边已走到头
        if (node.left == null) {
            return node.value;
        }
        return doMin(node.left);
    }
非递归实现 ★

  由于之前使用的是尾递归实现，所以下面转化为迭代法，代码如下：

    /**
     * 
查找最小关键字对应值

     * 非递归实现
     *
     * @return 关键字对应的值
     */
    public Object min() {
        return min(root);
    }

    private Object min(BSTNode node) {
        if (node == null) {
            return null;
        }
        BSTNode p = node;
        // 左边未走到头
        while (p.left != null) {
            p = p.left;
        }
        return p.value;
    }

  方法测试代码如下：

    public static void main(String[] args) {
        /*
                     4
                   /   \
                  2     6
                 / \   / \
                1   3 5   7
         */
        BSTNode n1 = new BSTNode(1, "Ray1");
        BSTNode n3 = new BSTNode(3, "Ray3");
        BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);

        BSTNode n5 = new BSTNode(5, "Ray5");
        BSTNode n7 = new BSTNode(7, "Ray7");
        BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);
        
        BSTNode root = new BSTNode(4, "Ray4", n2, n6);

        BSTTree tree = new BSTTree();
        tree.root = root;

        System.out.println(tree.min()); 

    }

  运行结果如下，查找到最小（最左节点）索引key为1的存储值Ray1，符合预期：

	Ray1

2.4 实现查找最大方法max()

  max()方法查找最大关键字key的对应存储值

递归实现

  与min()方法实现的思想类似，树中最右的节点即为最大索引（关键字），即向右走到头即可，所以只要右孩子为null，即找到最大关键字，使用递归实现的代码如下：

    /**
     * 
查找最大关键字对应值

     * 递归实现
     *
     * @return 关键字对应的值
     */
    public Object max() {
        return doMax(root);
    }

    public Object doMax(BSTNode node) {
        if (node == null) {
            return null;
        }
        // 右边已走到头
        if (node.right == null) {
            return node.value;
        }
        return doMax(node.right);
    }
非递归实现 ★

  由于之前使用的是尾递归实现，所以下面转化为迭代法，代码如下：

    /**
     * 
查找最大关键字对应值

     *
     * @return 关键字对应的值
     */
    public Object max() {
        return max(root);
    }

    private Object max(BSTNode node) {
        if (node == null) {
            return null;
        }
        BSTNode p = node;
        while (p.right != null) {
            p = p.right;
        }
        return p.value;
    }

  方法测试代码如下：

    public static void main(String[] args) {
        BSTNode n1 = new BSTNode(1, "Ray1");
        BSTNode n3 = new BSTNode(3, "Ray3");
        BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);

        BSTNode n5 = new BSTNode(5, "Ray5");
        BSTNode n7 = new BSTNode(7, "Ray7");
        BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);
        
        BSTNode root = new BSTNode(4, "Ray4", n2, n6);

        BSTTree tree = new BSTTree();
        tree.root = root;

        System.out.println(tree.max());

    }

  运行结果如下，查找到最大（最右节点）索引key为7的存储值Ray7，符合预期：

	Ray7

2.5 实现新增方法put(int key, Object value)

  新增put(int key, Object value)方法存储关键字和对应值，和Java中的Map的put方法类似，分为两种情况：

  1️⃣ key在整个树中已经存在，新增操作变为更新操作，将旧的值替换为新的值
  2️⃣ key在整个树中未存在，执行新增操作，将key value添加到树中

递归实现

  递归实现思路如下：

  • 若找到 key，走 else 更新找到节点的值
  • 若没找到 key，走第一个 if，创建并返回新节点
    • 返回的新节点，作为上次递归时 node 的左孩子或右孩子
    • 缺点是，会有很多不必要的赋值操作
    /**
     * 
存储关键字和对应值

     * 递归实现
     *
     * @param key   关键字
     * @param value 值
     */
    public void put(int key, Object value) {
        root = doPut(root, key, value);
    }

    private BSTNode doPut(BSTNode node, int key, Object value) {
        if (node == null) {
            return new BSTNode(key, value);
        }
        if (key < node.key) {
            node.left = doPut(node.left, key, value);
        } else if (node.key < key) {
            node.right = doPut(node.right, key, value);
        } else {
            node.value = value;
        }
        return node;
    }

  缺点：此处return node返回当前节点会多出一些额外的赋值动作。如下面这颗二叉搜索树，1作为插入节点，1和2通过node.left = doPut(node.left, key, value);建立父子关系返回，这是有必要的，但是由于递归，2和5也会通过node.left = doPut(node.left, key, value);建立父子关系，这样就是没必要的（因为5和2原本就存在父子关系），如果树的深度很大，那就会浪费很多性能。

        5
       / \
      2   6
        \   \
    1    3   7
非递归实现 ★

  查找逻辑和get方法的逻辑基本一样，区别是如果查找到值则更新node.value = value;，没查找到则新增。在新增时为了防止频繁的更新操作，添加parent父节点，判断新增节点是父节点的左孩子还是右孩子，然后再新增，代码如下：

    /**
     * 
存储关键字和对应值

     * 非递归实现
     *
     * @param key   关键字
     * @param value 值
     */
    public void put(int key, Object value) {
        BSTNode node = root;
        BSTNode parent = null; // 父节点
        while (node != null) {
            parent = node;
            if (key < node.key) {
                node = node.left;
            } else if (node.key < key) {
                node = node.right;
            } else {
                // 1. key 存在则更新
                node.value = value;
                return;
            }
        }
        // 2. key 不存在则新增，判断新节点是父节点的左孩子还是右孩子
        // parent 为空代表树为空的情况，那新增节点就是根节点
        if (parent == null) {
            root = new BSTNode(key, value);
        }
        // 新增节点为左孩子
        else if (key < parent.key) {
            parent.left = new BSTNode(key, value);
        }
        // 新增节点为右孩子
        else {
            parent.right = new BSTNode(key, value);
        }
    }

  测试代码：

    public static void main(String[] args) {
        /*
                     4
                   /   \
                  2     6
                 / \   / \
                1   3 5   7
         */
        BSTNode n1 = new BSTNode(1, "Ray1");
        BSTNode n3 = new BSTNode(3, "Ray3");
        BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);

        BSTNode n5 = new BSTNode(5, "Ray5");
        BSTNode n7 = new BSTNode(7, "Ray7");
        BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);
        BSTNode root = new BSTNode(4, "Ray4", n2, n6);

        BSTTree createTree = new BSTTree();
        createTree.root = root;


        BSTTree tree = new BSTTree();
        tree.put(4, new Object());
        tree.put(2, new Object());
        tree.put(6, new Object());
        tree.put(1, new Object());
        tree.put(3, new Object());
        tree.put(5, new Object());
        tree.put(7, new Object());
        System.out.println(createTree == tree);

        tree.put(1, "Ray486");
        System.out.println(tree.get(1).equals("Ray486"));


    }

  两树的key一致但输出false，说明不是同样的树，索引1的存储值被成功替换，均符合预期，测试结果如下：

	false
	true

2.6 实现查找关键字的前任值predecessor(int key)

  回顾跳转前驱后继

  一个节点的前驱（前任）节点是指：比它小的节点中，最大的那个

  一个节点的后继（后任）节点是指：比它大的节点中，最小的那个

瑞_数据结构与算法_二叉搜索树_第4张图片

  例如上图中

  • 1 没有前驱，后继是 2
  • 2 前驱是 1，后继是 3
  • 3 前驱是 2，后继是 4

  想要找到二叉搜索树的某节点的前驱后继节点，简单（但不高效）的办法是中序遍历，即可获得排序结果，此时很容易找到前驱后继。因为使用中序遍历后二叉搜索树的值就是升序的，有了升序排序，前驱后继节点就很好找。但是，由于中序遍历的性能不高，所以不推荐使用。

  要效率更高，需要研究一下规律，找前驱分成以下 2 种情况：

  1️⃣节点 有 左子树，此时前驱节点就是左子树的最大值，图中属于这种情况的有：

  • 2 的前驱是1
  • 4 的前驱是 3
  • 6 的前驱是 5
  • 7 的前驱是 6

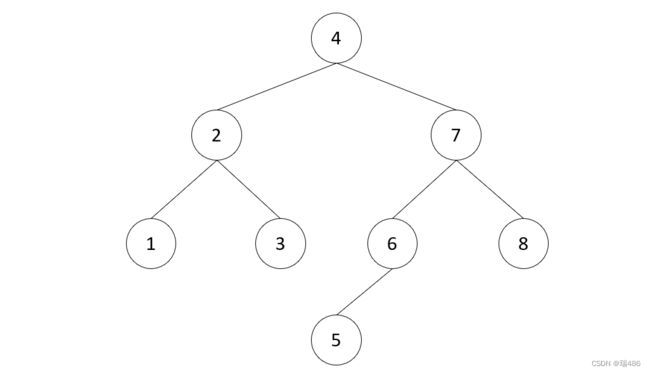
  2️⃣节点 没有 左子树，若离它最近的祖先自从左而来，此祖先即为前驱，如：

  • 3 的祖先 2 自左而来，前驱 2
  • 5 的祖先 4 自左而来，前驱 4
  • 8 的祖先 7 自左而来，前驱 7
  • 1 没有这样的祖先，前驱 null

瑞：祖先不止是父节点，也可以是父节点的父节点，父节点的的父节点的父节点…

  对于情况2，只需要添加一个指针，记录最近一个自左而来的祖先即可，实现代码如下：

    /**
     * 
查找关键字的前任值

     *
     * @param key 关键字
     * @return 前任值
     */
    public Object predecessor(int key) {
        BSTNode p = root;
        // 自左而来的祖先
        BSTNode ancestorFromLeft = null;
        while (p != null) {
            if (key < p.key) {
                p = p.left;
            } else if (p.key < key) {
                // 记录自左而来的祖先
                ancestorFromLeft = p;
                p = p.right;
            } else {
                break;
            }
        }
        // 没找到节点
        if (p == null) {
            return null;
        }
        // 找到节点 情况1：节点有左子树，此时前任就是左子树的最大值
        if (p.left != null) {
            return max(p.left);
        }
        // 找到节点 情况2：节点没有左子树，若离它最近的、自左而来的祖先就是前任
        return ancestorFromLeft != null ?
                ancestorFromLeft.value : null;
    }

2.7 查找关键字的后任值successor(int key)

  回顾跳转前驱后继

  一个节点的前驱（前任）节点是指：比它小的节点中，最大的那个

  一个节点的后继（后任）节点是指：比它大的节点中，最小的那个

瑞_数据结构与算法_二叉搜索树_第5张图片

  与前驱类似找后继也分成 2 种情况：

  1️⃣节点有右子树，此时后继节点即为右子树的最小值，如：

  • 2 的后继 3
  • 3 的后继 4
  • 5 的后继 6
  • 7 的后继 8

  2️⃣节点没有右子树，若离它最近的祖先自右而来，此祖先即为后继，如：

  • 1 的祖先 2 自右而来，后继 2
  • 4 的祖先 5 自右而来，后继 5
  • 6 的祖先 7 自右而来，后继 7
  • 8 没有这样的祖先，后继 null

  代码实现和前任类似，如下：

    /**
     * 
查找关键字的后任值

     *
     * @param key 关键字
     * @return 后任值
     */
    public Object successor(int key) {
        BSTNode p = root;
        // 自右而来的祖先
        BSTNode ancestorFromRight = null;
        while (p != null) {
            if (key < p.key) {
                // 记录自右而来的祖先
                ancestorFromRight = p;
                p = p.left;
            } else if (p.key < key) {
                p = p.right;
            } else {
                break;
            }
        }
        // 没找到节点
        if (p == null) {
            return null;
        }
        // 找到节点 情况1：节点有右子树，此时后任就是右子树的最小值
        if (p.right != null) {
            return min(p.right);
        }
        // 找到节点 情况2：节点没有右子树，若离它最近的、自右而来的祖先就是后任
        return ancestorFromRight != null ?
                ancestorFromRight.value : null;
    }

2.8 根据关键字删除remove(int key)

  删除remove(int key)方法需要考虑的情况较多。要删除某节点（称为 D），必须先找到被删除节点的父节点，这里称为 Parent，具体情况如下：

  1. 删除节点没有左孩子，将右孩子托孤给 Parent
  2. 删除节点没有右孩子，将左孩子托孤给 Parent
  3. 删除节点左右孩子都没有，已经被涵盖在情况1、情况2 当中，把 null 托孤给 Parent
  4. 删除节点左右孩子都有，可以将它的后继节点（称为 S）托孤给 Parent，设 S 的父亲为 SP，又分两种情况
    1. SP 就是被删除节点，此时 D 与 S 紧邻，只需将 S 托孤给 Parent
    2. SP 不是被删除节点，此时 D 与 S 不相邻，此时需要将 S 的后代托孤给 SP，再将 S 托孤给 Parent

  删除本身很简单，只要通过索引查找到该节点删除即可，但是，由于需要料理后事，所以想要做好删除操作，需要处理好“托孤”操作。

非递归实现 ★

  情况3走情况1或者情况2的逻辑都是可以的，所以不用管，主要是情况4的第二种子情况（删除和后继不相邻），需要处理好该情况下要删除节点的后任的托孤（利用后继节点不会有左孩子，如果有左孩子，那就不会是最小值，所以后继不可能有左孩子），再将后继节点托孤给被删除节点的父节点，代码如下：

/**
 * 
根据关键字删除

 * 非递归实现
 *
 * @param key 关键字
 * @return 被删除关键字对应值
 */
public Object remove(int key) {
    BSTNode p = root;
    // 记录待删除节点的父亲
    BSTNode parent = null;
    while (p != null) {
        if (key < p.key) {
            parent = p;
            p = p.left;
        } else if (p.key < key) {
            parent = p;
            p = p.right;
        } else {
            break;
        }
    }
    if (p == null) {
        return null;
    }
    // 删除操作
    if (p.left == null) {
        shift(parent, p, p.right); // 情况1
    } else if (p.right == null) {
        shift(parent, p, p.left); // 情况2
    } else {
        // 情况4
        // 4.1 被删除节点找后继
        BSTNode s = p.right;
        BSTNode sParent = p; // 后继父亲
        while (s.left != null) {
            sParent = s;
            s = s.left;
        }
        // 4.2 删除和后继不相邻, 处理后继的后事
        if (sParent != p) {                
            shift(sParent, s, s.right); // 不可能有左孩子（否则就不是后继节点）
            s.right = p.right;
        }
        // 4.3 后继取代被删除节点
        shift(parent, p, s);
        s.left = p.left;
    }
    return p.value;
}

/**
 * 托孤方法
 *
 * @param parent  被删除节点的父亲
 * @param deleted 被删除节点
 * @param child   被顶上去的节点
 */
// 只考虑让 n1父亲的左或右孩子指向 n2, n1自己的左或右孩子并未在方法内改变
private void shift(BSTNode parent, BSTNode deleted, BSTNode child) {
    if (parent == null) {
        // 根节点（特殊情况）
        root = child;
    } else if (deleted == parent.left) {
        parent.left = child;
    } else {
        parent.right = child;
    }
}

  测试代码：

    public static void main(String[] args) {

        /*
                     4
                   /   \
                  2     7
                 / \   /
                1   3 6
                     /
                    5
         */
        BSTNode n1 = new BSTNode(1, 1);
        BSTNode n3 = new BSTNode(3, 3);
        BSTNode n2 = new BSTNode(2, 2, n1, n3);

        BSTNode n5 = new BSTNode(5, 5);
        BSTNode n6 = new BSTNode(6, 6, n5, null);
        BSTNode n7 = new BSTNode(7, 7, n6, null);
        BSTNode root1 = new BSTNode(4, 4, n2, n7);

        BSTTree tree1 = new BSTTree();
        tree1.root = root1;

        Object delete = tree1.remove(7);
        System.out.println(delete + "\t" + 7); // 7     7

        // 删除后

         /*
                     4
                   /   \
                  2     6
                 / \   /
                1   3 5
         */
        BSTNode x1 = new BSTNode(1, 1);
        BSTNode x3 = new BSTNode(3, 3);
        BSTNode x2 = new BSTNode(2, 2, x1, x3);
        BSTNode x5 = new BSTNode(5, 5);
        BSTNode x6 = new BSTNode(6, 6, x5, null);
        BSTNode root2 = new BSTNode(4, 4, x2, x6);
        BSTTree tree2 = new BSTTree();
        tree2.root = root2;

        System.out.println(isSameTree(tree1.root,tree2.root)); // true

    }
    
    // 判断是否为同一树（key对应的value都相等）
    static boolean isSameTree(BSTNode tree1, BSTNode tree2) {
        if (tree1 == null && tree2 == null) {
            return true;
        }
        if (tree1 == null || tree2 == null) {
            return false;
        }
        if (tree1.key != tree2.key) {
            return false;
        }
        return isSameTree(tree1.left, tree2.left) && isSameTree(tree1.right, tree2.right);
    }

  测试结果如下，删除的元素符合预期，且删除后的树与预期结果的结构一致

	7	7
	true
递归实现

  由于递归实现效率低，且较难理解，主要是为了结合非递归实现提供思路，可以结合注释思考，不过多讲解，代码如下：

    /**
     * 
根据关键字删除

     * 递归实现
     *
     * @param key 关键字
     * @return 被删除关键字对应值
     */
    public Object remove(int key) {
        ArrayList<Object> result = new ArrayList<>(); // 保存被删除节点的值
        root = doRemove(root, key, result);
        return result.isEmpty() ? null : result.get(0);
    }

    /**
     * 私有 递归删除具体实现细节
     *
     * @param node   起点
     * @param key    删除索引
     * @param result 保存被删除节点的值
     * @return node 删剩下的孩子(找到) 或 null(没找到)
     * @author LiaoYuXing-Ray 2024/1/25 19:59
     **/
    private BSTNode doRemove(BSTNode node, int key, ArrayList<Object> result) {
        if (node == null) {
            return null;
        }
        if (key < node.key) {
            node.left = doRemove(node.left, key, result);
            return node;
        }
        if (node.key < key) {
            node.right = doRemove(node.right, key, result);
            return node;
        }
        result.add(node.value);
        if (node.left == null) { // 情况1 - 只有右孩子
            return node.right;
        }
        if (node.right == null) { // 情况2 - 只有左孩子
            return node.left;
        }
        BSTNode s = node.right; // 情况3 - 有两个孩子
        while (s.left != null) {
            s = s.left;
        }
        s.right = doRemove(node.right, s.key, new ArrayList<>());
        s.left = node.left;
        return s;
    }

  说明

  1. ArrayList result 用来保存被删除节点的值
  2. 第二、第三个 if 对应没找到的情况，继续递归查找和删除，注意后续的 doRemove返回值代表删剩下的，因此需要更新
  3. 最后一个 return 对应删除节点只有一个孩子的情况，返回那个不为空的孩子，待删节点自己因没有返回而被删除
  4. 第四个 if 对应删除节点有两个孩子的情况，此时需要找到后继节点，并在待删除节点的右子树中删掉后继节点，最后用后继节点替代掉待删除节点返回，别忘了改变后继节点的左右指针

    5. 3 二叉搜索树——范围查询

                 4
           /   \
          2     6
         / \   / \
        1   3 5   7

    3.1 找所有小于索引的值less(int key)

      less(int key)方法：找 < key 的所有 value

      使用中序遍历

        // 找 < key 的所有 value
    public List<Object> less(int key) {
        ArrayList<Object> result = new ArrayList<>();
        BSTNode p = root;
        LinkedList<BSTNode> stack = new LinkedList<>();
        while (p != null || !stack.isEmpty()) {
            if (p != null) {
                stack.push(p);
                p = p.left;
            } else {
                BSTNode pop = stack.pop();
                // 处理值
                if (pop.key < key) {
                    result.add(pop.value);
                } else {
                    break;
                }
                p = pop.right;
            }
        }
        return result;
    }

    3.2 找所有大于索引的值greater(int key)

      greater(int key)方法：找 > key 的所有 value

      使用常规的中序遍历（从左向右的中序遍历）

    public List<Object> greater(int key) {
    ArrayList<Object> result = new ArrayList<>();
    BSTNode p = root;
    LinkedList<BSTNode> stack = new LinkedList<>();
    while (p != null || !stack.isEmpty()) {
        if (p != null) {
            stack.push(p);
            p = p.left;
        } else {
            BSTNode pop = stack.pop();
            if (pop.key > key) {
                result.add(pop.value);
            }
            p = pop.right;
        }
    }
    return result;
}

      中序遍历效率不高，可以用 RNL 遍历（中序遍历的逆操作）

      注：

    • Pre-order, NLR
    • In-order, LNR
    • Post-order, LRN
    • Reverse pre-order, NRL（反向前序遍历，值右左）
    • Reverse in-order, RNL（反向中序遍历，右值左）
    • Reverse post-order, RLN（反向后续序遍历，右左值）

      RNL 遍历代码如下：

    // 找 > key 的所有 value
public List<Object> greater(int key) {
    ArrayList<Object> result = new ArrayList<>();
    BSTNode p = root;
    LinkedList<BSTNode> stack = new LinkedList<>();
    while (p != null || !stack.isEmpty()) {
        if (p != null) {
            stack.push(p);
            p = p.right;
        } else {
            BSTNode pop = stack.pop();
            if (pop.key > key) {
                result.add(pop.value);
            } else {
                break;
            }
            p = pop.left;
        }
    }
    return result;
}

    3.3 找范围值between(int key1, int key2)

      between(int key1, int key2)方法：找 >= key1 且 <= key2 的所有值

        // 找 >= key1 且 <= key2 的所有值
    public List<Object> between(int key1, int key2) {
        ArrayList<Object> result = new ArrayList<>();
        BSTNode p = root;
        LinkedList<BSTNode> stack = new LinkedList<>();
        while (p != null || !stack.isEmpty()) {
            if (p != null) {
                stack.push(p);
                p = p.left;
            } else {
                BSTNode pop = stack.pop();
                // 处理值
                if (pop.key >= key1 && pop.key <= key2) {
                    result.add(pop.value);
                } else if (pop.key > key2) {
                    break;
                }
                p = pop.right;
            }
        }
        return result;
    }

      测试：

        public static void main(String[] args) {
        /*
                 4
               /   \
              2     6
             / \   / \
            1   3 5   7
         */
        BSTNode n1 = new BSTNode(1, 1);
        BSTNode n3 = new BSTNode(3, 3);
        BSTNode n2 = new BSTNode(2, 2, n1, n3);

        BSTNode n5 = new BSTNode(5, 5);
        BSTNode n7 = new BSTNode(7, 7);
        BSTNode n6 = new BSTNode(6, 6, n5, n7);
        BSTNode root = new BSTNode(4, 4, n2, n6);

        BSTTree tree = new BSTTree();
        tree.root = root;

        System.out.println(tree.less(6));
        System.out.println(tree.greater(6));
        System.out.println(tree.between(3,5));
    }

      输出如下，符合预期

    	[1, 2, 3, 4, 5]
	[7]
	[3, 4, 5]

    3.3 小结

    优点：

    1. 如果每个节点的左子树和右子树的大小差距不超过一，可以保证搜索操作的时间复杂度是 O(log n)，效率高。
    2. 插入、删除结点等操作也比较容易实现，效率也比较高。
    3. 对于有序数据的查询和处理，二叉查找树非常适用，可以使用中序遍历得到有序序列。

    缺点：

    1. 如果输入的数据是有序或者近似有序的，就会出现极度不平衡的情况，可能导致搜索效率下降，时间复杂度退化成O(n)。
    2. 对于频繁地插入、删除操作，需要维护平衡二叉查找树，例如红黑树、AVL 树等，否则搜索效率也会下降。
    3. 对于存在大量重复数据的情况，需要做相应的处理，否则会导致树的深度增加，搜索效率下降。
    4. 对于结点过多的情况，由于树的空间开销较大，可能导致内存消耗过大，不适合对内存要求高的场景。

    瑞：关于二叉搜索树的练习可以结合《瑞_力扣LeetCode_二叉搜索树相关题》



    本文是博主的粗浅理解，可能存在一些错误或不完善之处，如有遗漏或错误欢迎各位补充，谢谢

      如果觉得这篇文章对您有所帮助的话，请动动小手点波关注，你的点赞收藏⭐️转发评论都是对博主最好的支持~


    你可能感兴趣的:(数据结构与算法,java,数据结构,二叉搜索树)

    • Long类型前后端数据不一致 igotyback 前端
      响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
    • LocalDateTime 转 String igotyback java开发语言
      importjava.time.LocalDateTime;importjava.time.format.DateTimeFormatter;publicclassMain{publicstaticvoidmain(String[]args){//获取当前时间LocalDateTimenow=LocalDateTime.now();//定义日期格式化器DateTimeFormatterformat
    • Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类qt开发语言sdl2linux
      需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
    • DIV+CSS+JavaScript技术制作网页（旅游主题网页设计与制作）云南大理 STU学生网页设计 网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
      ️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业：【HTML5网页期末作业(1000套)】程序员有趣的告白方式：【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面：计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
    • 【华为OD机试真题2023B卷 JAVA&JS】We Are A Team 若博豆 java算法华为javascript
      华为OD2023（B卷）机试题库全覆盖，刷题指南点这里WeAreATeam时间限制：1秒|内存限制：32768K|语言限制：不限题目描述：总共有n个人在机房，每个人有一个标号（1<=标号<=n），他们分成了多个团队，需要你根据收到的m条消息判定指定的两个人是否在一个团队中，具体的：1、消息构成为：abc，整数a、b分别代
    • 数组去重 好奇的猫猫猫
      整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
    • 关于城市旅游的HTML网页设计——(旅游风景云南 5页)HTML+CSS+JavaScript 二挡起步 web前端期末大作业javascripthtmlcss旅游风景
      ⛵源码获取文末联系✈Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业|游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作|HTML期末大学生网页设计作业，Web大学生网页HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScrip
    • HTML网页设计制作大作业（div+css） 云南我的家乡旅游景点 带文字滚动 二挡起步 web前端期末大作业web设计网页规划与设计htmlcssjavascriptdreamweaver前端
      Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript：做与用户的交互行为文章目录前端学习路线
    • node.js学习 小猿L node.jsnode.js学习vim
      node.js学习实操及笔记温故node.js，node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础，三大框架vuereactangular离不开node.jsnode.js是什么官网：node.js是一个开源的、跨平台的运行JavaScript的运行
    • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
      leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
    • Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redisbootstrap数据库
      1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
    • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
      Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
    • 数据结构之哈希表 X同学的开始 数据结构数据结构散列表
      哈希表(散列表)出现的原因在顺序表中查找时，需要从表头开始，依次遍历比较a[i]与key的值是否相等，直到相等才返回索引i；在有序表中查找时，我们经常使用的是二分查找，通过比较key与a[i]的大小来折半查找，直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是，这两种方法的效率都依赖于查找中比较的次数。我们有一种想法，能不能不经过比较，而是直接通过关键字key一次得到所要的结果呢？这时，
    • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
      Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
    • Java 重写(Override)与重载(Overload) 叨唧唧的
      Java重写(Override)与重载(Overload)重写(Override)重写是子类对父类的允许访问的方法的实现过程进行重新编写,返回值和形参都不能改变。即外壳不变，核心重写！重写的好处在于子类可以根据需要，定义特定于自己的行为。也就是说子类能够根据需要实现父类的方法。重写方法不能抛出新的检查异常或者比被重写方法申明更加宽泛的异常。例如：父类的一个方法申明了一个检查异常IOExceptio
    • 简单了解 JVM 记得开心一点啊 jvm
      目录♫什么是JVM♫JVM的运行流程♫JVM运行时数据区♪虚拟机栈♪本地方法栈♪堆♪程序计数器♪方法区/元数据区♫类加载的过程♫双亲委派模型♫垃圾回收机制♫什么是JVMJVM是JavaVirtualMachine的简称，意为Java虚拟机。虚拟机是指通过软件模拟的具有完整硬件功能的、运行在一个完全隔离的环境中的完整计算机系统（如：JVM、VMwave、VirtualBox）。JVM和其他两个虚拟机
    • 1分钟解决 -bash: mvn: command not found，在Centos 7中安装Maven Energet!c 开发语言
      1分钟解决-bash:mvn:commandnotfound，在Centos7中安装Maven检查Java环境1下载Maven2解压Maven3配置环境变量4验证安装5常见问题与注意事项6总结检查Java环境Maven依赖Java环境，请确保系统已经安装了Java并配置了环境变量。可以通过以下命令检查：java-version如果未安装，请先安装Java。1下载Maven从官网下载：前往Apach
    • Java企业面试题3 马龙强_ java
      1.break和continue的作用(智*图)break：用于完全退出一个循环（如for,while）或一个switch语句。当在循环体内遇到break语句时，程序会立即跳出当前循环体，继续执行循环之后的代码。continue：用于跳过当前循环体中剩余的部分，并开始下一次循环。如果是在for循环中使用continue，则会直接进行条件判断以决定是否执行下一轮循环。2.if分支语句和switch分
    • JVM、JRE和 JDK：理解Java开发的三大核心组件 Y雨何时停T Javajava
      Java是一门跨平台的编程语言，它的成功离不开背后强大的运行环境与开发工具的支持。在Java的生态中，JVM（Java虚拟机）、JRE（Java运行时环境）和JDK（Java开发工具包）是三个至关重要的核心组件。本文将探讨JVM、JDK和JRE的区别，帮助你更好地理解Java的运行机制。1.JVM：Java虚拟机（JavaVirtualMachine）什么是JVM？JVM，即Java虚拟机，是Ja
    • Java面试题精选：消息队列(二) 芒果不是芒 Java面试题精选javakafka
      一、Kafka的特性1.消息持久化：消息存储在磁盘，所以消息不会丢失2.高吞吐量：可以轻松实现单机百万级别的并发3.扩展性：扩展性强，还是动态扩展4.多客户端支持：支持多种语言（Java、C、C++、GO、）5.KafkaStreams（一个天生的流处理）:在双十一或者销售大屏就会用到这种流处理。使用KafkaStreams可以快速的把销售额统计出来6.安全机制：Kafka进行生产或者消费的时候会
    • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
      文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
    • 白骑士的Java教学基础篇 2.5 控制流语句 白骑士所长 Java教学java开发语言
      欢迎继续学习Java编程的基础篇！在前面的章节中，我们了解了Java的变量、数据类型和运算符。接下来，我们将探讨Java中的控制流语句。控制流语句用于控制程序的执行顺序，使我们能够根据特定条件执行不同的代码块，或重复执行某段代码。这是编写复杂程序的基础。通过学习这一节内容，你将掌握如何使用条件语句和循环语句来编写更加灵活和高效的代码。条件语句条件语句用于根据条件的真假来执行不同的代码块。if语句‘
    • python语法——三目运算符 HappyRocking pythonpython三目运算符
      在java中，有三目运算符，如：intc=(a>b)?a:b表示c取两者中的较大值。但是在python，不能直接这样使用，估计是因为冒号在python有分行的关键作用。那么在python中，如何实现类似功能呢？可以使用ifelse语句，也是一行可以完成，格式为：aifbelsec表示如果b为True，则表达式等于a，否则等于c。如：c=(aif(a>b)elseb)同样是完成了取最大值的功能。
    • [Python] 数据结构 详解及代码 AIAdvocate 算法python数据结构链表
      今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
    • ArrayList 源码解析 程序猿进阶 Java基础ArrayListListjava面试性能优化架构设计idea
      ArrayList是Java集合框架中的一个动态数组实现，提供了可变大小的数组功能。它继承自AbstractList并实现了List接口，是顺序容器，即元素存放的数据与放进去的顺序相同，允许放入null元素，底层通过数组实现。除该类未实现同步外，其余跟Vector大致相同。每个ArrayList都有一个容量capacity，表示底层数组的实际大小，容器内存储元素的个数不能多于当前容量。当向容器中添
    • 4.C_数据结构_队列 荣世蓥 数据结构数据结构
      概述什么是队列：队列是限定在两端进行插入操作和删除操作的线性表。具有先入先出(FIFO)的特点相关名词：队尾：写入数据的一段队头：读取数据的一段空队：队列中没有数据，队头指针=队尾指针满队：队列中存满了数据，队尾指针+1=队头指针循环队列1、基本内容循环队列是以数组形式构成的队列数据结构。循环队列的结构体如下：typedefintdata_t;//队列数据类型#defineN64//队列容量typ
    • Java爬虫框架（一）--架构设计 狼图腾-狼之传说 java框架java任务html解析器存储电子商务
      一、架构图那里搜网络爬虫框架主要针对电子商务网站进行数据爬取，分析，存储，索引。爬虫：爬虫负责爬取，解析，处理电子商务网站的网页的内容数据库：存储商品信息索引：商品的全文搜索索引Task队列：需要爬取的网页列表Visited表：已经爬取过的网页列表爬虫监控平台：web平台可以启动，停止爬虫，管理爬虫，task队列，visited表。二、爬虫1.流程1)Scheduler启动爬虫器，TaskMast
    • Java：爬虫框架 dingcho Javajava爬虫
      一、ApacheNutch2【参考地址】Nutch是一个开源Java实现的搜索引擎。它提供了我们运行自己的搜索引擎所需的全部工具。包括全文搜索和Web爬虫。Nutch致力于让每个人能很容易,同时花费很少就可以配置世界一流的Web搜索引擎.为了完成这一宏伟的目标,Nutch必须能够做到:每个月取几十亿网页为这些网页维护一个索引对索引文件进行每秒上千次的搜索提供高质量的搜索结果简单来说Nutch支持分
    • python怎么将png转为tif_png转tif weixin_39977276
      发国外的文章要求图片是tif，cmyk色彩空间的。大小尺寸还有要求。比如网上大神多，找到了一段代码，感谢！https://www.jianshu.com/p/ec2af4311f56https://github.com/KevinZc007/image2Tifimportjava.awt.image.BufferedImage;importjava.io.File;importjava.io.Fi
    • JavaScript 中，深拷贝（Deep Copy）和浅拷贝（Shallow Copy） 跳房子的前端 前端面试javascript开发语言ecmascript
      在JavaScript中，深拷贝（DeepCopy）和浅拷贝（ShallowCopy）是用于复制对象或数组的两种不同方法。了解它们的区别和应用场景对于避免潜在的bugs和高效地处理数据非常重要。以下是对深拷贝和浅拷贝的详细解释，包括它们的概念、用途、优缺点以及实现方式。1.浅拷贝（ShallowCopy）概念定义：浅拷贝是指创建一个新的对象或数组，其中包含了原对象或数组的基本数据类型的值和对引用数
    • mongodb3.03开启认证 21jhf mongodb
      下载了最新mongodb3.03版本，当使用--auth 参数命令行开启mongodb用户认证时遇到很多问题，现总结如下： （百度上搜到的基本都是老版本的，看到db.addUser的就是，请忽略） Windows下我做了一个bat文件，用来启动mongodb，命令行如下： mongod --dbpath db\data --port 27017 --directoryperdb --logp
    • 【Spark103】Task not serializable bit1129 Serializable
      Task not serializable是Spark开发过程最令人头疼的问题之一，这里记录下出现这个问题的两个实例，一个是自己遇到的，另一个是stackoverflow上看到。等有时间了再仔细探究出现Task not serialiazable的各种原因以及出现问题后如何快速定位问题的所在，至少目前阶段碰到此类问题，没有什么章法 1.   package spark.exampl
    • 你所熟知的 LRU(最近最少使用) dalan_123 java
      关于LRU这个名词在很多地方或听说，或使用，接下来看下lru缓存回收的实现 1、大体的想法     a、查询出最近最晚使用的项     b、给最近的使用的项做标记 通过使用链表就可以完成这两个操作，关于最近最少使用的项只需要返回链表的尾部；标记最近使用的项，只需要将该项移除并放置到头部，那么难点就出现 你如何能够快速在链表定位对应的该项？ 这时候多
    • Javascript 跨域 周凡杨 JavaScriptjsonp跨域cross-domain
                                         
    • linux下安装apache服务器 g21121 apache
      安装apache 下载windows版本apache，下载地址：http://httpd.apache.org/download.cgi   1.windows下安装apache Windows下安装apache比较简单，注意选择路径和端口即可，这里就不再赘述了。 2.linux下安装apache： 下载之后上传到linux的相关目录，这里指定为/home/apach
    • FineReport的JS编辑框和URL地址栏语法简介 老A不折腾 finereportweb报表报表软件语法总结
        JS编辑框： 1.FineReport的js。 作为一款BS产品，browser端的JavaScript是必不可少的。 FineReport中的js是已经调用了finereport.js的。 大家知道，预览报表时，报表servlet会将cpt模板转为html，在这个html的head头部中会引入FineReport的js，这个finereport.js中包含了许多内置的fun
    • 根据STATUS信息对MySQL进行优化 墙头上一根草 status
      mysql  查看当前正在执行的操作，即正在执行的sql语句的方法为:      show processlist 命令   mysql> show global status;可以列出MySQL服务器运行各种状态值，我个人较喜欢的用法是show status like '查询值%';一、慢查询mysql> show variab
    • 我的spring学习笔记7-Spring的Bean配置文件给Bean定义别名 aijuans Spring 3
      本文介绍如何给Spring的Bean配置文件的Bean定义别名？ 原始的 <bean id="business" class="onlyfun.caterpillar.device.Business"> <property name="writer"> <ref b
    • 高性能mysql 之 性能剖析 annan211 性能mysqlmysql 性能剖析剖析
      1 定义性能优化 mysql服务器性能，此处定义为 响应时间。 在解释性能优化之前，先来消除一个误解，很多人认为，性能优化就是降低cpu的利用率或者减少对资源的使用。 这是一个陷阱。 资源时用来消耗并用来工作的，所以有时候消耗更多的资源能够加快查询速度，保持cpu忙绿，这是必要的。很多时候发现 编译进了新版本的InnoDB之后，cpu利用率上升的很厉害，这并不
    • 主外键和索引唯一性约束 百合不是茶 索引唯一性约束主外键约束联机删除
      目标;第一步;创建两张表 用户表和文章表         第二步;发表文章       1,建表; ---用户表 BlogUsers --userID唯一的 --userName --pwd --sex create
    • 线程的调度 bijian1013 java多线程thread线程的调度java多线程
      1.       Java提供一个线程调度程序来监控程序中启动后进入可运行状态的所有线程。线程调度程序按照线程的优先级决定应调度哪些线程来执行。   2.       多数线程的调度是抢占式的（即我想中断程序运行就中断，不需要和将被中断的程序协商） a) 
    • 查看日志常用命令 bijian1013 linux命令unix
      一.日志查找方法，可以用通配符查某台主机上的所有服务器grep "关键字" /wls/applogs/custom-*/error.log   二.查看日志常用命令1.grep '关键字' error.log：在error.log中搜索'关键字'2.grep -C10 '关键字' error.log：显示关键字前后10行记录3.grep '关键字' error.l
    • 【持久化框架MyBatis3一】MyBatis版HelloWorld bit1129 helloworld
      MyBatis这个系列的文章，主要参考《Java Persistence with MyBatis 3》。   样例数据 本文以MySQL数据库为例，建立一个STUDENTS表，插入两条数据，然后进行单表的增删改查     CREATE TABLE STUDENTS ( stud_id int(11) NOT NULL AUTO_INCREMENT,
    • 【Hadoop十五】Hadoop Counter bit1129 hadoop
         1. 只有Map任务的Map Reduce Job File System Counters FILE: Number of bytes read=3629530 FILE: Number of bytes written=98312 FILE: Number of read operations=0 FILE: Number of lar
    • 解决Tomcat数据连接池无法释放 ronin47 tomcat 连接池　优化
      近段时间，公司的检测中心报表系统(SMC)的开发人员时不时找到我，说用户老是出现无法登录的情况。前些日子因为手头上 有Jboss集群的测试工作，发现用户不能登录时，都是在Tomcat中将这个项目Reload一下就好了，不过只是治标而已，因为大概几个小时之后又会 再次出现无法登录的情况。 今天上午，开发人员小毛又找到我，要我协助将这个问题根治一下，拖太久用户难保不投诉。 简单分析了一
    • java-75-二叉树两结点的最低共同父结点 bylijinnan java
      import java.util.LinkedList; import java.util.List; import ljn.help.*; public class BTreeLowestParentOfTwoNodes { public static void main(String[] args) { /* * node data is stored in
    • 行业垂直搜索引擎网页抓取项目 carlwu LuceneNutchHeritrixSolr
      公司有一个搜索引擎项目，希望各路高人有空来帮忙指导，谢谢！ 这是详细需求： （1） 通过提供的网站地址(大概100-200个网站)，网页抓取程序能不断抓取网页和其它类型的文件（如Excel、PDF、Word、ppt及zip类型），并且程序能够根据事先提供的规则，过滤掉不相干的下载内容。 （2） 程序能够搜索这些抓取的内容，并能对这些抓取文件按照油田名进行分类，然后放到服务器不同的目录中。
    • [通讯与服务]在总带宽资源没有大幅增加之前,不适宜大幅度降低资费 comsci 资源
            降低通讯服务资费，就意味着有更多的用户进入，就意味着通讯服务提供商要接待和服务更多的用户，在总体运维成本没有由于技术升级而大幅下降的情况下，这种降低资费的行为将导致每个用户的平均带宽不断下降，而享受到的服务质量也在下降，这对用户和服务商都是不利的。。。。。。。。     &nbs
    • Java时区转换及时间格式 Cwind java
      本文介绍Java API 中 Date, Calendar, TimeZone和DateFormat的使用，以及不同时区时间相互转化的方法和原理。   问题描述： 向处于不同时区的服务器发请求时需要考虑时区转换的问题。譬如，服务器位于东八区（北京时间，GMT+8:00），而身处东四区的用户想要查询当天的销售记录。则需把东四区的“今天”这个时间范围转换为服务器所在时区的时间范围。
    • readonly,只读，不可用 dashuaifu jsjspdisablereadOnlyreadOnly
      readOnly 和 readonly 不同，在做js开发时一定要注意函数大小写和jsp黄线的警告！！！我就经历过这么一件事： 使用readOnly在某些浏览器或同一浏览器不同版本有的可以实现“只读”功能，有的就不行，而且函数readOnly有黄线警告！！！就这样被折磨了不短时间！！！（期间使用过disable函数，但是发现disable函数之后后台接收不到前台的的数据！！！）  
    • LABjs、RequireJS、SeaJS 介绍 dcj3sjt126com jsWeb
      LABjs 的核心是 LAB（Loading and Blocking）：Loading 指异步并行加载，Blocking 是指同步等待执行。LABjs 通过优雅的语法（script 和 wait）实现了这两大特性，核心价值是性能优化。LABjs 是一个文件加载器。RequireJS 和 SeaJS 则是模块加载器，倡导的是一种模块化开发理念，核心价值是让 JavaScript 的模块化开发变得更
    • [应用结构]入口脚本 dcj3sjt126com PHPyii2
      入口脚本 入口脚本是应用启动流程中的第一环，一个应用（不管是网页应用还是控制台应用）只有一个入口脚本。终端用户的请求通过入口脚本实例化应用并将将请求转发到应用。 Web 应用的入口脚本必须放在终端用户能够访问的目录下，通常命名为 index.php，也可以使用 Web 服务器能定位到的其他名称。 控制台应用的入口脚本一般在应用根目录下命名为 yii（后缀为.php），该文
    • haoop shell命令 eksliang hadoophadoop shell
      cat chgrp chmod chown copyFromLocal copyToLocal cp du dus expunge get getmerge ls lsr mkdir movefromLocal mv put rm rmr setrep stat tail test text
    • MultiStateView不同的状态下显示不同的界面 gundumw100 android
      只要将指定的view放在该控件里面，可以该view在不同的状态下显示不同的界面，这对ListView很有用，比如加载界面，空白界面，错误界面。而且这些见面由你指定布局，非常灵活。 PS：ListView虽然可以设置一个EmptyView，但使用起来不方便，不灵活，有点累赘。 <com.kennyc.view.MultiStateView xmlns:android=&qu
    • jQuery实现页面内锚点平滑跳转 ini JavaScripthtmljqueryhtml5css
      平时我们做导航滚动到内容都是通过锚点来做，刷的一下就直接跳到内容了，没有一丝的滚动效果，而且 url 链接最后会有“小尾巴”，就像#keleyi，今天我就介绍一款 jquery 做的滚动的特效，既可以设置滚动速度，又可以在 url 链接上没有“小尾巴”。   效果体验：http://keleyi.com/keleyi/phtml/jqtexiao/37.htmHTML文件代码： &
    • kafka offset迁移 kane_xie kafka
      在早前的kafka版本中（0.8.0），offset是被存储在zookeeper中的。   到当前版本（0.8.2）为止，kafka同时支持offset存储在zookeeper和offset manager（broker）中。   从官方的说明来看，未来offset的zookeeper存储将会被弃用。因此现有的基于kafka的项目如果今后计划保持更新的话，可以考虑在合适
    • android > 搭建 cordova 环境 mft8899 android
        1 , 安装 node.js        http://nodejs.org      node -v   查看版本   2, 安装 npm   可以先从  https://github.com/isaacs/npm/tags  下载 源码 解压到
    • java封装的比较器，比较是否全相同，获取不同字段名字 qifeifei
       非常实用的java比较器，贴上代码： import java.util.HashSet; import java.util.List; import java.util.Set; import net.sf.json.JSONArray; import net.sf.json.JSONObject; import net.sf.json.JsonConfig; i
    • 记录一些函数用法 .Aky. 位运算PHP数据库函数IP
      高手们照旧忽略。 想弄个全天朝IP段数据库，找了个今天最新更新的国内所有运营商IP段，copy到文件，用文件函数，字符串函数把玩下。分割出startIp和endIp这样格式写入.txt文件，直接用phpmyadmin导入.csv文件的形式导入。（生命在于折腾，也许你们觉得我傻X，直接下载人家弄好的导入不就可以，做自己的菜鸟，让别人去说吧） 当然用到了ip2long()函数把字符串转为整型数
    • sublime text 3 rust wudixiaotie Sublime Text
      1.sublime text 3 => install package => Rust 2.cd ~/.config/sublime-text-3/Packages 3.mkdir rust 4.git clone https://github.com/sp0/rust-style 5.cd rust-style 6.cargo build --release 7.ctrl