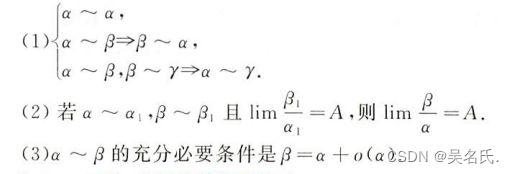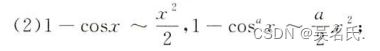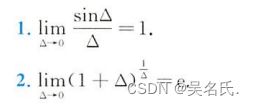高等数学基础【1】极限与连续
第一节 函数
一、基本概念
①函数
设变量x的取值范围为D,若对任意的x∈D,按照某种对应关系总有唯一确定的值y与x对应,称y为x的函数,记为y=f(z),其中D称为函数y=f(x)的定义域
②复合函数
设u=φ(x)(x∈D1),y=f(u)(u∈D,),且对任意的x∈D1有φ(x)∈D2,称y为x的复合函数,记为y=f[φ(x)]
③反函数
设y=f(x)(x∈D)为单调函数,其值域为f(D),对任意的y∈f(D),有唯一确定的x∈D与之对应,称x为y的反函数,记为x=f^-1(y)
④基本初等函数
⑤初等函数
由常数及基本初等函数经过有限次的四则运算和复合运算而成的式子构成的函数称为初等函数
二、函数的初等特性
①有界性
设y = f(x)(x ∈ D),若存在M>0,对任意的x∈D,总有|f(x)|≤M,称函数f(x)在D上有界
注意:
(1)若存在常数M1,对任意的x∈D,有f(x)≥M1,称f(x)在D上有下界;若存在常数M2,对任意的x∈D,有f(x)≤M2,称f(x)在D上有上界
(2)若|f(x)|≤2,则f(x)≥-2且f(x)≤2,即若f(x)有界,则f(x)既有下界又有上界;反之,若f(x)≥-2且f(x)≤4,则|f(x)|≤4,即若f(x)既有下界又有上界,则f(x)有界,故f(x)有界的充分必要条件是f(x)既有下界又有上界
②单调性
设y=f(x)(x ∈ D),若对任意的x1,x2∈D且x1
③奇偶性
设y≡f(x)(x∈D),其中D关于原点对称,若f(-x)=-f(x),称y=f(x)在D上为奇函数;若f(-x)=f(x),称y=f(x)在D上为偶函数
④周期性
设y=f(x)(x∈ D),若存在T>0,对任意的x∈D,x+T∈D,有f(x+T)=f(x),称y=f(x)为周期函数,T称为y=f(x)的周期
三、特殊函数
①符号函数
②狄利克雷函数
R\Q表示有理数集在实数集中的余集
③取整函数
称y=[x]为取整函数,其函数值为x左侧最大的整数值,若x为整数,则函数值即为x,如:[-√2]=-2,[√5]=2,[3]=3
注意:
(1)[x]≤x
(2)[x+y]=[x]+[y]不是总成立的,但[x+m]=[x]+m(其中m为整数)是一定成立的
第二节 极限
一、基本概念
①极限的定义
注意:
②无穷小
(1)无穷小的定义
(2)无穷小的比较
二、极限性质
(一)极限的一般性质
定理1(极限的唯一性) 若极限存在,则极限一定是唯一的
定理4(列极限与子列极限的关系)
(1)若列极限存在,则该列的任一子列存在相同的极限
(2)若某一子列极限存在,则该列极限不一定存在
注意:
(二)极限的四则远算
①四则运算性质
设limf(x)=A,limg(x)=B,则
(1)lim[f(x)±g(x)]=A±B;
(2)limf(x)g(x)=AB
(3)limf(x)/g(x)=A/B(B≠0)
注意:若limf(x)或limg(x)不存在,则极限的四则运算性质不成立
②复合函数极限运算性质
注意:
(三)极限存在准则
①迫敛定理(夹逼定理)
②单调有界的数列必有极限
(四)无穷小的性质
①无穷小的基本性质
②等价无穷小的性质
③x→0时,常用的等价无穷小
(1)x ~ sinx ~ tanx ~ arcsinx ~ arctanx ~ ln(x+1) ~ e^x-1
(3)(1+x)^a-1 ~ ax
(4)a^x-1 ~ xlna
二、两个重要极限
利用两个极限存在准则,可以得到在极限计算过程中非常重要的两个极限:
注意:
第三节 连续与间断
一、基本概念
①函数连续性概念
注意:
②间断点及分类
二、闭区间上连续函数的性质
矩阵笔记
①n项和或积的极限计算的一般方法
(1)先计算和或积,再计算极限.
(2)夹逼定理(分子或分母次数不齐时,一般使用夹逼定理)
(3)定积分的定义(分子及分母次数都齐时,使用定积分定义求极限)