DS Wannabe之5-AM Project: DS 30day int prep day1

Q1. What is the difference between AI, Data Science, ML, and DL?

Artificial Intelligence: AI is purely math and scientific exercise, but when it became computational, it started to solve human problems formalized into a subset of computer science. Artificial intelligence has changed the original computational statistics paradigm to the modern idea that machines could mimic actual human capabilities, such as decision making and performing more “human” tasks. Modern AI into two categories

1. General AI - Planning, decision making, identifying objects, recognizing sounds, social & business transactions

2. Applied AI - driverless/ Autonomous car or machine smartly trade stocks

Machine Learning: Instead of engineers “teaching” or programming computers to have what they need to carry out tasks, that perhaps computers could teach themselves – learn something without being explicitly programmed to do so. ML is a form of AI where based on more data, and they can change actions and response, which will make more efficient, adaptable and scalable. e.g., navigation apps and recommendation engines. Classified into: supervised, unsupervised, reinforcement learning.

Data Science: Data science has many tools, techniques, and algorithms called from these fields, plus others –to handle big data

The goal of data science, somewhat similar to machine learning, is to make accurate predictions and to automate and perform transactions in real-time, such as purchasing internet traffic or automatically generating content.

Data science relies less on math and coding and more on data and building new systems to process the data. Relying on the fields of data integration, distributed architecture, automated machine learning, data visualization, data engineering, and automated data-driven decisions, data science can cover an entire spectrum of data processing, not only the algorithms or statistics related to data.

Deep Learning: It is a technique for implementing ML.

ML provides the desired output from a given input, but DL reads the input and applies it to another data. In ML, we can easily classify the flower based upon the features. Suppose you want a machine to look at an image and determine what it represents to the human eye, whether a face, flower, landscape, truck, building, etc.

Machine learning is not sufficient for this task because machine learning can only produce an output from a data set – whether according to a known algorithm or based on the inherent structure of the data. You might be able to use machine learning to determine whether an image was of an “X” – a flower, say – and it would learn and get more accurate. But that output is binary (yes/no) and is dependent on the algorithm, not the data. In the image recognition case, the outcome is not binary and not dependent on the algorithm.

The neural network performs MICRO calculations with computational on many layers. Neural networks also support weighting data for ‘confidence. These results in a probabilistic system, vs. deterministic, and can handle tasks that we think of as requiring more ‘human-like’ judgment.

Q2. What is the difference between Supervised learning, Unsupervised learning and Reinforcement learning?

Machine Learning

Machine learning is the scientific study of algorithms and statistical models that computer systems use to effectively perform a specific task without using explicit instructions, relying on patterns and inference instead.

Supervised learning

In a supervised learning model, the algorithm learns on a labeled dataset, to generate reasonable predictions for the response to new data. (Forecasting outcome of new data)

• Regression
• Classification

Building a model by learning the patterns of historical data with some relationship between data to make a data-driven prediction.

Unsupervised learning

An unsupervised model, in contrast, provides unlabelled data that the algorithm tries to make sense of by extracting features, co-occurrence and underlying patterns on its own. We use unsupervised learning for

• Clustering
• Anomaly detection
• Association
• Autoencoders

Reinforcement Learning

Reinforcement learning is less supervised and depends on the learning agent in determining the output solutions by arriving at different possible ways to achieve the best possible solution.

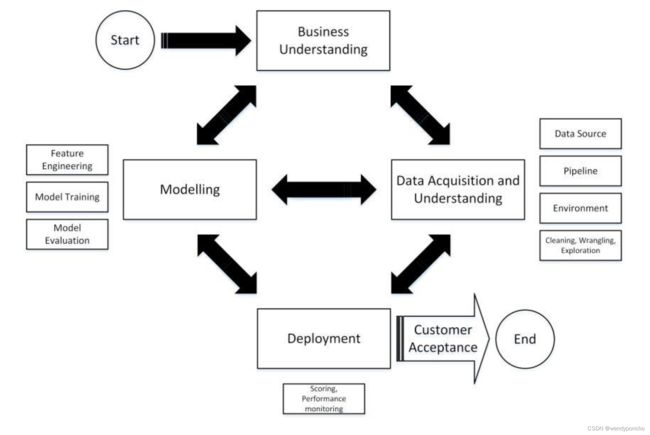
Q3. Describe the general architecture of Machine learning.

Business understanding: Understand the give use case, and also, it's good to know more about the domain for which the use cases are built.

Data Acquisition and Understanding: Data gathering from different sources and understanding the data. Cleaning the data, handling the missing data if any, data wrangling, and EDA( Exploratory data analysis).

Modeling: Feature Engineering - scaling the data, feature selection - not all features are important. We use the backward elimination method, correlation factors, PCA and domain knowledge to select the features.

Model Training based on trial and error method or by experience, we select the algorithm and train with the selected features.

Model evaluation Accuracy of the model , confusion matrix and cross-validation.
If accuracy is not high, to achieve higher accuracy, we tune the model...either by changing the algorithm used or by feature selection or by gathering more data, etc.

Deployment - Once the model has good accuracy, we deploy the model either in the cloud or Rasberry py or any other place. Once we deploy, we monitor the performance of the model.if its good...we go live with the model or reiterate the all process until our model performance is good.

Q4. What is Linear Regression?

Linear Regression tends to establish a relationship between a dependent variable(Y) and one or more independent variable(X) by finding the best fit of the straight line.

The equation for the Linear model is Y = mX+c, where m is the slope and c is the intercept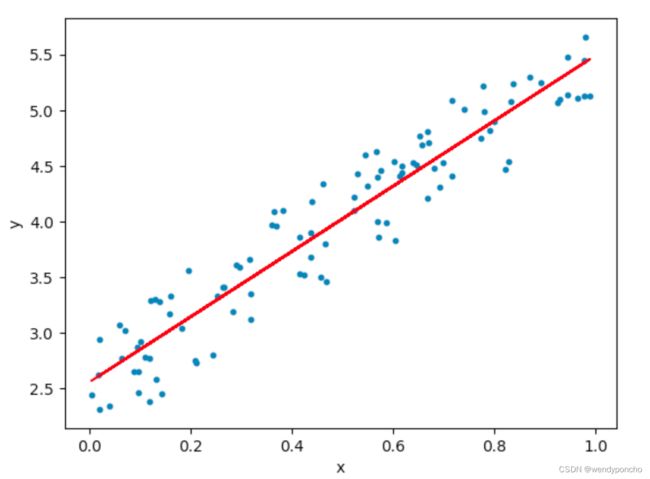

可参考我另外一篇ml prep有详细解释lr。

In the above diagram, the blue dots we see are the distribution of 'y' w.r.t 'x.' There is no straight line that runs through all the data points. So, the objective here is to fit the best fit of a straight line that will try to minimize the error between the expected and actual value.

Q5. OLS Stats Model (Ordinary Least Square) 

OLS is a stats model, which will help us in identifying the more significant features that can has an influence on the output. OLS model in python is executed as:

lm = smf.ols(formula = 'Sales ~ am+constant', data = data).fit() lm.conf_int() lm.summary()

And we get the output as below,

The higher the t-value for the feature, the more significant the feature is to the output variable. And also, the p-value plays a rule in rejecting the Null hypothesis(Null hypothesis stating the features has zero significance on the target variable.). If the p-value is less than 0.05(95% confidence interval) for a feature, then we can consider the feature to be significant.

Q6. What is L1 Regularization (L1 = lasso) ?

The main objective of creating a model(training data) is making sure it fits the data properly and reduce the loss. Sometimes the model that is trained which will fit the data but it may fail and give a poor performance during analyzing of data (test data). This leads to overfitting. Regularization came to overcome overfitting.

Lasso Regression (Least Absolute Shrinkage and Selection Operator) adds “Absolute value of magnitude” of coefficient, as penalty term to the loss function.

插播一些基础知识

Lasso and Elastic Net

What Are Lasso and Elastic Net?

Lasso is a regularization technique. Use lasso to:

• Reduce the number of predictors in a regression model.

• Identify important predictors.

• Select among redundant predictors.

• Produce shrinkage estimates with potentially lower predictive errors than ordinary least squares.

Elastic net is a related technique. Use elastic net when you have several highly correlated variables. lasso provides elastic net regularization when you set the Alpha name-value pair to a number strictly between 0 and 1.

Overview of Lasso and Elastic Net

Lasso is a regularization technique for performing linear regression. Lasso includes a penalty term that constrains the size of the estimated coefficients. Therefore, it resembles ridge regression. Lasso is a shrinkage estimator: it generates coefficient estimates that are biased to be small. Nevertheless, a lasso estimator can have smaller mean squared error than an ordinary least-squares estimator when you apply it to new data.

Unlike ridge regression, as the penalty term increases, lasso sets more coefficients to zero. This means that the lasso estimator is a smaller model, with fewer predictors. As such, lasso is an alternative to stepwise regression and other model selection and dimensionality reduction techniques.

Elastic net is a related technique. Elastic net is a hybrid of ridge regression and lasso regularization. Like lasso, elastic net can generate reduced models by generating zero-valued coefficients. Empirical studies have suggested that the elastic net technique can outperform lasso on data with highly correlated predictors.

Q7. L2 Regularization(L2 = Ridge Regression)

L2 regularization (also known as ridge regularization)

adds a penalty term to the objective function that is proportional to the square of the coefficients of the model. This penalty term shrinks the coefficients toward zero, （Ridge regularization forces the weights to be small but does not make them zero and does not give the sparse solution.）

Methods like Cross-validation, Stepwise Regression are there to handle overfitting and perform feature selection work well with a small set of features. These techniques are good when we are dealing with a large set of features.

Along with shrinking coefficients, the lasso performs feature selection, as well. (Remember the ‘selection‘ in the lasso full-form?) Because some of the coefficients become exactly zero, which is equivalent to the particular feature being excluded from the model.

If lambda is zero, then it is equivalent to OLS. But if lambda is very large, then it will add too much weight, and it will lead to under-fitting.

Ridge is not robust to outliers as square terms blow up the error differences of the outliers, and the regularization term tries to fix it by penalizing the weights

Ridge regression performs better when all the input features influence the output, and all with weights are of roughly equal size.

L2 regularization can learn complex data patterns.

Q8. What is R square(where to use and where not)?

R-squared is a statistical measure of how close the data are to the fitted regression line. It is also known as the coefficient of determination, or the coefficient of multiple determination for multiple regression.

The definition of R-squared is the percentage of the response variable variation that is explained by a linear model.

R-squared = Explained variation / Total variation
R-squared is always between 0 and 100%.
0% indicates that the model explains none of the variability of the response data around its mean. 100% indicates that the model explains all the variability of the response data around its mean.
In general, the higher the R-squared, the better the model fits your data.

There is a problem with the R-Square. The problem arises when we ask this question to ourselves.** Is it good to help as many independent variables as possible?**

The answer is No because we understood that each independent variable should have a meaningful impact. But, even** if we add independent variables which are not meaningful**, will it improve R-Square value?

So, we calculate the Adjusted R-Square with a better adjustment in the formula of generic R-square. 调整R平方来补充R平方的不足。调整R平方对于模型中独立变量的数量进行了惩罚，可以提供一个更为全面和准确的模型评估。

Q9. What is Mean Square Error?

The mean squared error tells you how close a regression line is to a set of points. It does this by taking the distances from the points to the regression line (these distances are the “errors”) and squaring them.

The line equation is y=Mx+B. We want to find M (slope) and B (y-intercept) that minimizes the squared error.

均方误差（Mean Square Error, MSE）是衡量模型预测值与实际观测值之间差异的一种指标。具体来说，它通过计算每个观测点到回归线的距离（这些距离被称为“误差”），然后将这些误差的值平方，最后求平均值得到。均方误差的计算公式如下：

其中，n 是观测点的数量，yi​ 是第i个观测点的实际值，y^​i​ hat是第i个观测点的模型预测值。

均方误差越小，表明回归线与观测点之间的距离越小，即模型的预测值与实际观测值之间的差异越小，模型的拟合度越好。因此，均方误差是评估回归模型性能的常用指标之一。不过，值得注意的是，由于均方误差将误差平方，因此对于较大的误差值，其惩罚会比较重，这可能会导致模型过于关注那些具有较大误差的数据点。

Q10. Why Support Vector Regression? Difference between SVR and a simple regression model?

In simple linear regression, try to minimize the error rate. But in SVR, we try to fit the error within a certain threshold.

Main Concepts: 

1. Boundary
2. Kernel

3. Support Vector

4. Hyper Plane

Our best fit line is the one where the hyperplane has the maximum number of points.
We are trying to do here is trying to decide a decision boundary at ‘e’ distance from the original hyperplane such that data points closest to the hyperplane or the support vectors are within that boundary line

支持向量回归（Support Vector Regression, SVR）基于支持向量机（Support Vector Machines, SVM）的概念，SVM是分类任务中的一种强大工具。SVR调整了SVM的原理，使其适用于解决回归问题。以下是选择SVR的理由以及SVR与简单回归模型之间的主要区别：

为什么选择SVR？

1. 容忍边界（ε-不敏感区）： SVR引入了一种概念，即在一定的边界内的误差被认为是可以接受的。这个ε-不敏感区意味着模型可以忽略在指定范围内的误差，使得SVR对于数据中的离群值和噪声具有较强的鲁棒性。

2. 正则化参数： SVR具有正则化参数，允许控制在达到高边界和最小化训练误差之间的权衡。这使得SVR特别适用于避免过拟合，确保模型的复杂性与其在未见数据上的表现之间的平衡。

3. 非线性关系： 通过使用核函数，SVR能够在高维特征空间中有效地进行线性回归，使其能够捕捉数据中的复杂、非线性关系，而无需手动添加非线性特征。

4. 全局最优： SVR模型的解是全局唯一的，这得益于其凸优化的性质。这与某些可能受到局部最小值问题影响的回归模型形成对比。

SVR与简单回归模型的区别

1. 目标函数： 简单线性回归模型通常最小化预测值和实际值之间的平方误差之和。而SVR则侧重于最小化模型复杂性并确保误差在一定的边界内，这导致了一个不同的优化问题。

2. 误差处理： 在简单回归中，所有的误差都被同等对待，以二次方式贡献于损失。SVR提供了定义ε-不敏感区的灵活性，其中低于一定阈值的误差被忽略，这有助于处理离群值和噪声。

3. 处理非线性关系的灵活性： 虽然简单回归模型可能需要手动转换特征以建模非线性关系，但SVR可以使用核函数自动处理非线性，无需显式特征转换。

4. 正则化： SVR固有地包括正则化，它控制模型复杂性与其在训练数据上的表现之间的平衡。简单回归模型默认可能不包括正则化，可能需要额外的技术，如Ridge或Lasso回归，以纳入正则化。

总之，SVR提供了一种先进的回归方法，具有处理非线性、离群值的优势，并在模型复杂性与性能之间实现平衡，使其成为各种回归任务的多功能工具。

我们会在之后的hyperparameter tunning的部分回到这里。[Ridge regression and lasso both add a regularization term to linear regression; the weight for the regularization term is called the regularization parameter. Decision trees have hyperparameters such as the desired depth and number of leaves in the tree. Support vector machines (SVMs) require setting a misclassification penalty term. Kernelized SVMs require setting kernel parameters like the width for radial basis function (RBF) kernels. The list goes on.]