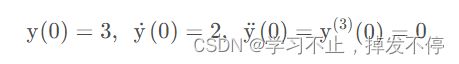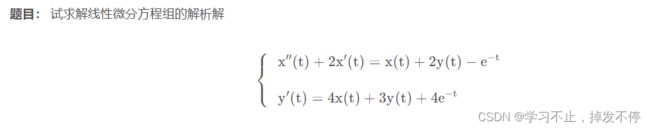微分方程应用(MATLAB)
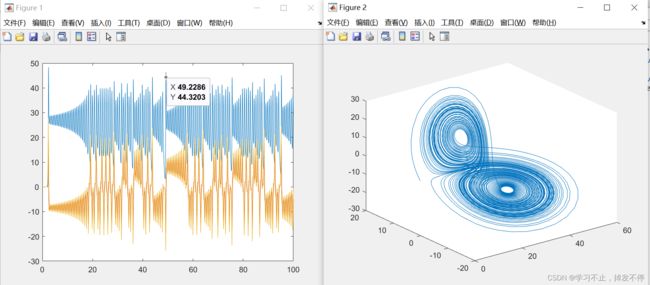
【例题1】matlab求解微分方程的解析解
close all
clear
clc
t_final = 100;
x0 = [0; 0; 1e-10];
f = @(t,x)[-8/3*x(1)+x(2)*x(3); -10*x(2)+10*x(3); -x(1)*x(2)+28*x(2)-x(3)];
[t,x] = ode45(f, [0,t_final], x0);
plot(t,x), figure;
plot3(x(:,1),x(:,2),x(:,3));
【例题2】微分方程解析解
close all
clear
clc
syms y(t);
u = exp(-5*t)*cos(2*t+1)+5;
uu = 5*diff(u,t,2) + 4*diff(u,t) + 2*u;
f(t) = diff(y,t,4) + 10*diff(y,t,3) + 35*diff(y,t,2) + 50*diff(y,t) + 24*y;
ySol = dsolve(f(t)==uu);
ySol = simplify(ySol);
(1)初值条件
close all
clear
clc
syms y(t);
u = exp(-5*t)*cos(2*t+1)+5;
uu = 5*diff(u,t,2) + 4*diff(u,t) + 2*u;
f(t) = diff(y,t,4) + 10*diff(y,t,3) + 35*diff(y,t,2) + 50*diff(y,t) + 24*y;
Dy=diff(y,t);
D2y=diff(y,t,2);
D3y=diff(y,t,3);
cond=[y(0)==3,Dy(0)==2, D2y(0)==0, D3y(0)==0];
ySol = dsolve(f(t)==uu,cond);
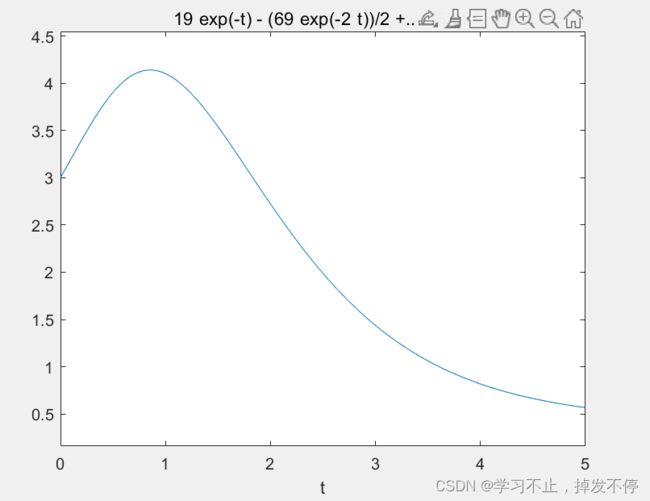
ySol = simplify(ySol);
ezplot(ySol,[0,5])【例题3】求解方程组
close all
clear
clc
syms x(t) y(t)
eqn1 = diff(x,t,2) + 2*diff(x,t) == x + 2*y(t) - exp(-t);
eqn2 = diff(y,t) == 4*x + 3*y(t) + 4*exp(-t);
[xSol, ySol] = dsolve([eqn1, eqn2]);
【例题3】
close all
clear
clc
eq1='Dx=2*x-3*y+3*z';
eq2='Dy=4*x-5*y+3*z';
eq3='Dz=4*x-4*y+2*z';
[x,y,z]=dsolve(eq1,eq2,eq3,'x(0)=1,y(0)=2,z(0)=1');%如果省略自变量,默认为t