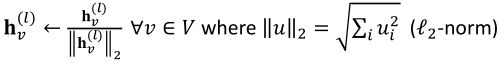《图机器学习》-GNN 《A Single Layer of a GNN》

一、A Single Layer of a GNN

单层的神经网络包括两个部分：

1. 消息转换(Message)
2. 信息聚合(Aggregation)

$$GNNLayer=Message+Aggregation$$

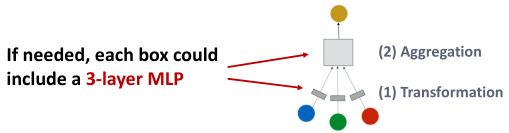
GNN Layer做的事情就是：
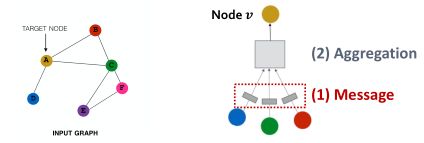
将一组向量压缩成一个向量，即根据一组邻居向量生成本节点的embedding。如下图；

---

Message computation

Message是消息在图的边上传递信息时进行的操作，即计算位置位于边上。

Message function表示为：

直觉:
每个节点将创建一条消息，该消息稍后将发送给其他节点。

最简单的消息转换函数可以是一个线性变换，如下图：

---

Aggregation

消息聚合一般位于消息传递之后，作用是将转换后的消息聚合成一个向量。

直观:
每个节点将聚集来自节点v的邻居的消息，以生成本节点的embedding。

Aggregation表示为：

常用的消息聚合函数如下：

• $m_u^{(l)}$:表示上一层embedding转换后的消息
  $h_v^{(l)}$:表示v的邻居节点消息$m_u^{(l)}$聚合后产生的本层v的embedding

---

上述的Aggregation存在的问题是：
没有使用节点本身的信息，所以节点本身的信息会丢失。(即不会记忆之前对该节点所了解到的信息)

解决方案：

1. 在进行消息转换时，节点本身也进行转换

   • 通常情况下，邻居节点和节点本身将执行不同的消息计算。
   • 如邻居节点会通过$W$矩阵进行消息转换，而节点本身会通过另一矩阵$B$进行消息转换
     

2. 在消息聚合时，加入本节点的$m_v^{(l)}$

   • 在从邻居聚合之后，可以聚合来自节点v本身的消息
   • 常用的操作有：concatenation、 summation
     

此外，可以引入非线性的激活函数，来增强GNN的表达能力。既可以在message处，也可以在aggregation处添加。

---

二、Classical GNN Layer

1、GCN

介绍一个经典的图卷积网络：GCN

其embedding公式如下：

将$W$矩阵移入到求和函数里，如下图；

• 红色虚线的部分时消息转换操作，进行了一个线性转换和归一化操作
• 黄色部分时消息聚合，进行的是sum操作
  

2、GraphSAGE

GraphSAGE建于GCN之上，但做了扩展。

其embedding公式如下：

该公式可以理解成两步聚合：
第一步：聚合邻居节点信息
第二步：在节点本身上进一步聚合

第一步的聚合函数AGG可以是：

• Mean：取邻居的加权平均值
  

• Pool：变换相邻向量并应用对称向量函数Mean(⋅)或Max(⋅)
  

• LSTM：应用LSTM来重新打乱邻居
  

个人理解：
这里的AGG其实是包含两个部分的，先转换再聚合。
如Pool：MLP就是转换，Mean是聚合。

在GraphSAGE的每一层$h_v^{(l)}$上都可以应用L2 Normalization。

• 没有L2归一化，嵌入向量对向量有不同的尺度(L2范数)
• 在某些情况下(并非总是如此)，嵌入的规范化会导致性能的提高
• L2归一化后，所有向量都有相同的L2范数

3、GAT

该模型在GCN的基础上引入了注意力机制，其公式如下：

这里的${\alpha }_{vu}$表示$u$节点提供的信息对本节点$v$的重要性

在GCN和GraphSAGE就有注意力的概念了：

• 在GCN和GraphSAGE中，${\alpha }_{vu}=\frac{1}{|N(v)|}$
• 但${\alpha }_{vu}$取决于$v$，而非$u$；即所有的邻居节点的都同等重要，所以它的作用非常有限。

但在实际情况中，并非所有的邻居节点都同等重要的；所有将注意力机制引入GNN，以量化不同节点对本节点信息的重要性。

将${\alpha }_{vu}$的计算公式记为$a$，可以基于节点的信息来计算注意力参数$e_{vu}$：

$e_{vu}$表示$u$的消息对节点$v$的重要性。

之后将$e_{vu}$进行归一化得到${\alpha }_{vu}$；可以使用softmax函数进行归一化将重要性置为区间0~1的数字。

得到${\alpha }_{vu}$后，基于注意力权重${\alpha }_{vu}$计算节点的embedding：

例子：

当然也可以通过其他形式得到${\alpha }_{vu}$；如将节点A和B的信息串联起来，当作输入通过一个简单的单层神经网络，最后输出$e_{vu}$；如下图：

$a$中的参数可以通过端到端的方式学习。

---

Multi-head attention：

多头注意力机制能够稳定注意机制的学习过程。

通过构造多个注意力得分(每个副本都有不同的参数集，即下面的每个初始化时都会赋予不同的参数),如下图：

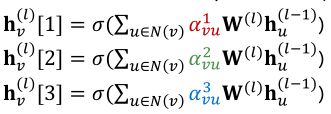
最后，再将上面的三个输出进行聚合：

---

注意力机制的好处：

• 允许(隐式地)为不同的邻居指定不同的重要性值【关键优点】
• 计算效率：
  • 注意系数的计算可以在图的所有边缘上并行进行
  • 聚合可以在所有节点上并行化
• 存储效率:
  • 稀疏矩阵操作不需要存储超过O(V + E)个条目
  • 固定数量的参数，与图的大小无关
• 只关注于本地网络社区
• 归纳能力：
  • 这是一种共享的边缘机制
  • 它不依赖于全局图结构

---

三、GNN Layer in Practice

许多现代深度学习模块可以合并到GNN层中：

• Batch Normalization：
  • 作用：稳定神经网络训练
• Dropout：
  • 防止过度拟合。迫使GNN对损坏的数据更加健壮
• Attention：
  • 控制信息的重要性
• 激活函数 ：
  

四、Stacking GNN Layers

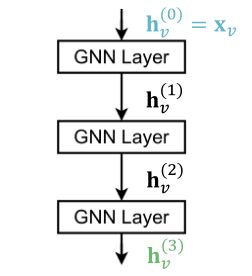
如何将单层的GNN组织成一个图神经网络？

可以将单层GNN按顺序进行堆叠；如下图，第一层输入是节点的feature $x_v$，最后一层的输出是节点的embedding $h_v^{(L)}$。

但当堆叠许多GNN层时，会出现过度平滑问题(the over-smoothing problem)。

过度平滑问题(the over-smoothing problem)：
所有节点嵌入收敛到相同的值。

这很糟糕，因为我们想使用节点嵌入来区分节点。为什么会发生这个问题呢？

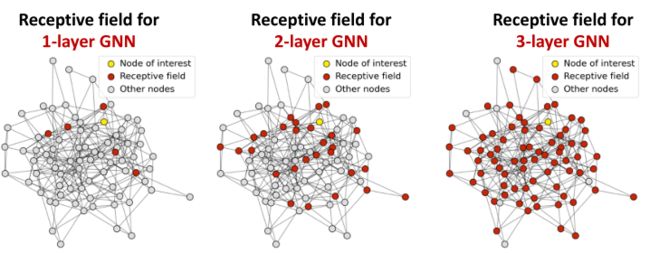
首先介绍接受域这个概念，接受域类似于CNN的感受野，是当节点在嵌入时感兴趣节点的集合【简单理解就是，在生成节点的嵌入时参考的节点】。如下图；

红色节点表示黄色节点在不同层下的接受域；在1-layer GNN时，黄色节点的接受域是与之相邻的邻居(1条可达的节点)；在2-layer GNN时，黄色节点的接受域是其两跳可达的邻居；
于此类推，在K层GNN中，每个节点都有一个K-hop邻域的接受域。

接下来通过接受域来解释过渡平滑问题，我们知道一个节点的嵌入是由它的接受野决定的，所以如果两个节点具有高度重叠的接受域，则它们的嵌入高度相似。

因此：
堆叠许多GNN layers➡节点接受域高度重合➡节点嵌入高度相似➡产生过度平滑问题

---

解决过度平滑问题：

• 添加GNN层时请谨慎
  • 与其他领域的神经网络(用于图像分类的CNN)不同，添加更多的GNN层并不总是有帮助的
  • 步骤：
    第一步：分析必要的接受域来解决你的问题。例如，通过计算图形的直径
    第二步：设置GNN层数L比接受域多一点。不要将L设置太大

---

过度平滑问题限制了GNN层数的添加，那么在GNN层数较少的情况下，如何增强浅层GNN的表达能力?

• 方式一：在GNN层中添加更多的表达能力

  • 如我们可以让聚合/转换成为一个深度神经网络。
    

• 方式二：添加不传递消息的层

  • 如GNN不一定只包含GNN层，可以在GNN层之前和之后添加MLP层(应用于每个节点)，作为预处理层和后处理层
    

---

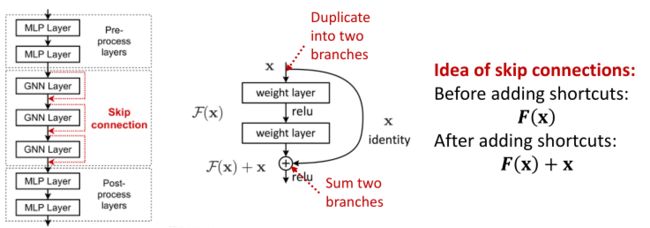
如果实际任务需要深层的GNN时，可以在在GNN中添加跳过连接。

因为早期GNN层中的节点嵌入有时可以更好地区分节点，所以可以通过在GNN中添加快捷方式来增加早期层对最终节点嵌入的影响。

为什么跳跃连接会有效？

跳跃连接创建了一个mixture of models，N个跳跃连接能够产生$2^N$种可能的路径，如下图；我们自动得到了shallow gnn和deep gnn的混合。

GCN使用跳跃连接的实例：

即将前一层的输入作为后面层的输入。

其他方式的跳跃连接：
直接跳到最后一层，最后一层直接从前一层中的所有节点嵌入中聚合。