滑动窗口入门(算法村第十六关青铜挑战)
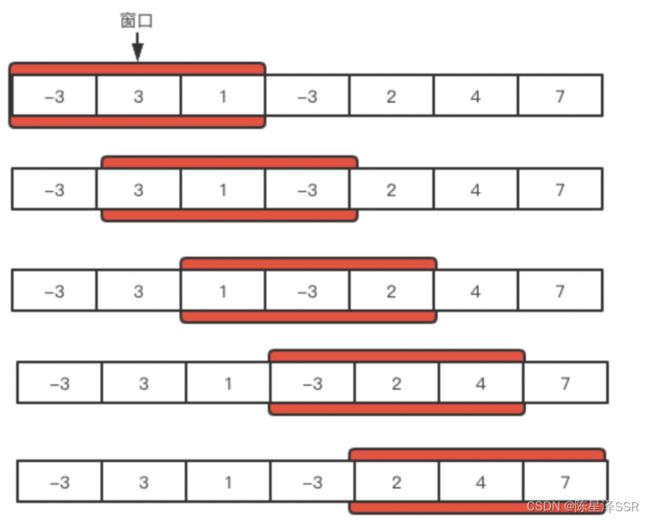
- 窗口:窗口其实就是两个变量left和ight之间的元素,也可以理解为一个区间。窗口大小可能固定,也可能变化。
- 滑动:窗口是移动的,事实上移动的仍然是left和ight两个变量,而不是序列中的元素。当变量移动的时,其中间的元素会发生变化。
滑动窗口题目本身没有太高的思维含量,但是实际在解题的时候仍然会感觉比较吃力,主要原因有以下几点:
- 解题最终要落实到数组上,特别是边界处理上,这是容易晕的地方,稍有疏忽就难以得到准确的结果。
- 有些元素的比较、判断等比较麻烦,不仅要借助集合等工具,而且处理过程中还有一些技巧,如果不熟悉会导致解题难度非常大。
- 堆!堆结构非常适合在流数据中找固定区间内的最大、最小等问题。因此滑动窗口经常和堆一起使用可以完美解决很多复杂的问题。
最后一个问题,那双指针和滑动窗口有啥区别?滑动窗口是双指针的一种类型,主要关注两个指针之间元素的情况,因此范围更小一些,而双指针的应用范围更大,花样也更多。
子数组最大平均数
643. 子数组最大平均数 I - 力扣(LeetCode)
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
任何误差小于 10^-5 的答案都将被视为正确答案。
示例 1:
输入:nums = [1,12,-5,-6,50,3], k = 4
输出:12.75
解释:最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
示例 2:
输入:nums = [5], k = 1
输出:5.00000
提示:
n == nums.length1 <= k <= n <= 105-104 <= nums[i] <= 104
大小固定的滑动窗口
public double findMaxAverage(int[] nums, int k)
{
//计算前k个的和
int windowSum = 0;
for(int i = 0; i < k; i++)
windowSum += nums[i];
int ans = windowSum;
//滑动窗口,右边加上一个则左边就减掉一个
for (int i = k; i < nums.length; i++)
{
windowSum = windowSum + nums[i] - nums[i - k];
ans = Math.max(ans, windowSum);
}
//返回平均值
return (double) ans / k;
}
最长连续递增序列
674. 最长连续递增序列 - 力扣(LeetCode)
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
提示:
1 <= nums.length <= 104-109 <= nums[i] <= 109
大小可变的滑动窗口
实现方式一
public int findLengthOfLCIS(int[] nums)
{
int left = 0;
int right = 0;
int ans = 0;
while (right < nums.length)
{
//若窗口右侧不满足严格递增条件,则left跳到right的位置重新开始计算
if(right > 0 && nums[right] <= nums[right - 1])
left = right;
//无论是否满足条件,right都先向右移动
right++;
ans = Math.max(ans, right - left); //维护最大的窗口大小
}
return ans;
}
实现方式二
public int findLengthOfLCIS(int[] nums)
{
int left = 0;
int ans = 1; //nums至少有一个元素,所以最长连续递增的子序列至少为1
for(int right = 1; right < nums.length; right++)
{
//若窗口右侧不满足严格递增条件,则left跳到right的位置重新开始计算
if(nums[right] <= nums[right - 1])
left = right;
ans = Math.max(ans, right - left + 1); //维护最大的窗口大小
}
return ans;
}