表达式求值——(运算符优先级、中缀表达式)
目录
一、理清思路
二、掌握基本的运算符优先级
三、中缀表达式的实现(不加括号)
四、中缀表达式的实现(加括号)
五、表达式求值——(经典栈应用)
一、理清思路
“表达式求值”问题,两个核心关键要素:(栈应用经典例子)(时间复杂度为O(n))
(1)双栈,一个操作数栈(num),一个运算符栈(op);
(2)运算符优先级;(栈顶运算符与即将入栈的运算符之间的优先级比较)
二、掌握基本的运算符优先级
1.对于+ 或 - 的优先数相等, 对于* 或 / 的优先数也是相等的;
2.但是对于同一个操作符op优先级比较, op[栈顶]>op[即将入栈];
运算符表如下所示:
对运算符表解释如下:
(1)如果栈顶是+,即将入栈的是+,栈顶优先级高,需要先计算,再入栈;
(2)如果栈顶是+,即将入栈的是*,栈顶优先级低,直接入栈;
(3)如果栈顶是*,即将入栈的是+,栈顶优先级高,需要先计算,再入栈;
(4)如果栈顶是*,即将入栈的是*,栈顶优先级高,需要先计算,再入栈;
(只要栈顶元素优先级大于等于即将入栈的优先级,就先计算,新运算符后入栈)
(只要栈顶元素优先级小于即将入栈的优先数级,新运算符就直接入栈)
三、中缀表达式的实现(不加括号)
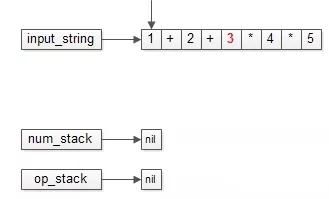
例子:1+2+3*4*5(借鉴于Hasity)
1、使用两个栈num_stack(寄存操作数)和op_stack(寄存运算符);
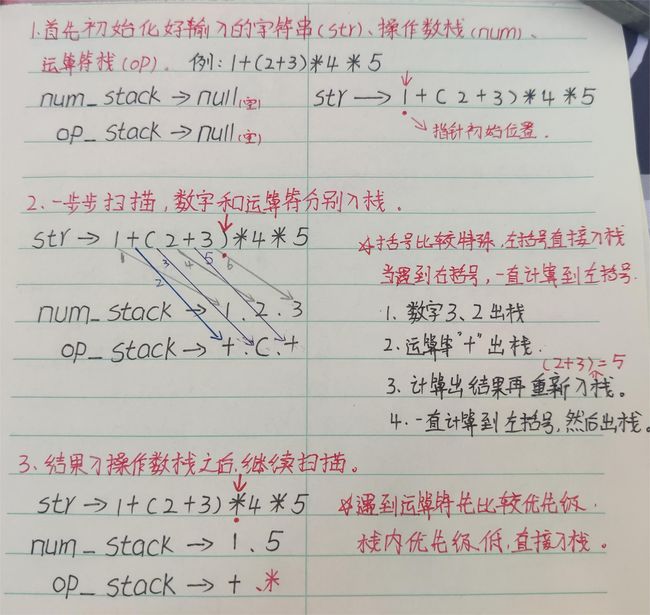
首先将其进行初始化;
2、接下来进行一步一步地扫描,操作数一个个入栈,运算符也入栈;
3、下一个操作符要入栈时,需要先比较优先级,栈内的优先级高,必须先计算,才能入栈。
计算流程为:
(1)操作数出栈,作为num2;
(2)操作数出栈,作为num1;
(3)运算符出栈,作为op;
(4)计算出结果(1+2=3),结果入操作数栈;
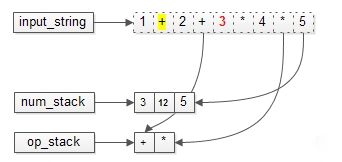
4、运算符和操作数继续入栈,当下一个操作符要入栈时,继续比较与栈顶的优先级;
5、栈内的优先级低,可以直接入栈;接下来字符串继续移动,继续比较优先级;
6、栈内的优先级高,需要先计算再入栈(3*4=12)再入栈;
7、运算符和操作数继续入栈,直至扫描完毕;
8、不断出栈,直到得到最终结果(3+60=63)算法完成;
四、中缀表达式的实现(加括号)
要点:括号分为两个运算符"( " 和 “ )”;
1、遇到 ( 说明会往下走, 所以只需将 ( 压栈;
2、遇到 ) 说明会往上走, 所以要计算括号内所有运算符, 所以要逆向计算运算符直至遇到 (;
样例:1+(2+3)*4*5
五、表达式求值——(经典栈应用)
题目描述:
给定一个表达式,其中运算符仅包含
+,-,*,/(加 减 乘 整除),可能包含括号,请你求出表达式的最终值;注意:
- 数据保证给定的表达式合法;
- 题目保证符号
-只作为减号出现,不会作为负号出现,例如,-1+2,(2+2)*(-(1+1)+2)之类表达式均不会出现;- 题目保证表达式中所有数字均为正整数;
- 题目保证表达式在中间计算过程以及结果中,均不超过 2^31;
- 题目中的整除是指向 0 取整,也就是说对于大于 0 的结果向下取整,例如 5/3=15/3=1,对于小于 0 的结果向上取整,例如 5/(1−4)=−15/(1−4)=−1;
- C++和Java中的整除默认是向零取整;Python中的整除
//默认向下取整,因此Python的eval()函数中的整除也是向下取整,在本题中不能直接使用;输入格式:
共一行,为给定表达式;
输出格式:
共一行,为表达式的结果;
数据范围:
表达式的长度不超过 10^5;
输入样例:
(2+2)*(1+1)输出样例:
8
详解代码如下:
#include
#include
#include
#include
using namespace std;
stack num;
stack op;
unordered_map h{ {'+', 1}, {'-', 1}, {'*',2}, {'/', 2} };//优先级表
//根据优先级表,我们可以继续列出{{'^',3}}运算符等等;
void eval()//求值
{
int a = num.top(); num.pop();//第二个操作数
//栈的性质:先进后出!!! a是第一个进但第二个被弹出,即为第二个操作数;
int b = num.top(); num.pop();//第一个操作数
char p = op.top(); op.pop();//运算符
int r = 0;//结果
if (p == '+') r = b + a;
if (p == '-') r = b - a;
if (p == '*') r = b * a;
if (p == '/') r = b / a;
num.push(r);//结果入栈
}
int main()
{
string s;
cin >> s;
for (int i = 0; i < s.size(); i++)
{
if (isdigit(s[i]))//如果是数字则数字入栈
{
int x = 0, j = i;//计算数字
while (j < s.size() && isdigit(s[j]))
{
x = x * 10 + s[j] - '0';//将字符串数字转化为十进制数字
j++;
}
num.push(x);//数字入栈
i = j - 1;
//当执行完while语句时会i++。如果i=j的话就相当于中间跳过去一个元素;
//只有当i=j-1时,i++之后,i指的位置是数字后面的非数字部分;
}
else if (s[i] == '(')//左括号无优先级,直接入栈
{
op.push(s[i]);
}
else if (s[i] == ')')//右括号特殊,遇到右括号计算括号里面所有的运算符
{
while (op.top() != '(') eval();//一直计算,直到出现左括号
op.pop();//左括号出栈
}
else
{
while (op.size() && h[op.top()] >= h[s[i]]) eval();//比较优先级
//while (h[op.top()] >= h[s[i]] && op.size())这是错的不能交换循环里的条件顺序
//如果不先判空而先取栈顶元素的话,栈可能为空,就取不到栈顶而判错
op.push(s[i]);//操作符入栈
}
}
while (op.size()) eval();//剩余的进行计算
cout << num.top() << endl;
return 0;
}
如果不了解unordered_map,这是对unordered_map的简介;
精简代码如下所示:
#include
#include
#include
#include
using namespace std;
stack num;
stack op;
unordered_map h{ {'+', 1}, {'-', 1}, {'*',2}, {'/', 2} };//优先级表
void eval()
{
int a = num.top();num.pop();
int b = num.top();num.pop();
char p = op.top();op.pop();
int r = 0;
if (p == '+') r = b + a;
if (p == '-') r = b - a;
if (p == '*') r = b * a;
if (p == '/') r = b / a;
num.push(r);
}
int main()
{
string s;
cin >> s;
for (int i = 0; i < s.size(); i++)
{
if (isdigit(s[i]))
{
int x = 0, j = i;
while (j < s.size() && isdigit(s[j]))
{
x = x * 10 + s[j] - '0';
j++;
}
num.push(x);
i = j - 1;
}
else if (s[i] == '(')
{
op.push(s[i]);
}
else if (s[i] == ')')
{
while (op.top() != '(') eval();
op.pop();
}
else
{
while (op.size() && h[op.top()] >= h[s[i]]) eval();
op.push(s[i]);
}
}
while (op.size()) eval();
cout << num.top() << endl;
return 0;
}