MYSQL的B+Tree索引树高度如何计算

我们使用MySQL数据库的时候，绝大部分的情况下在使用InnoDB存储引擎，偶尔会使用MyISAM存储引擎，至于其他存储引擎，我相信大家都很少接触到，甚至可能都没有听说过。所以本文只讲解InnoDB和MyISAM两个存储引擎的索引，以及如何计算这两个存储引擎的索引结构B+Tree的高度。

InnoDB

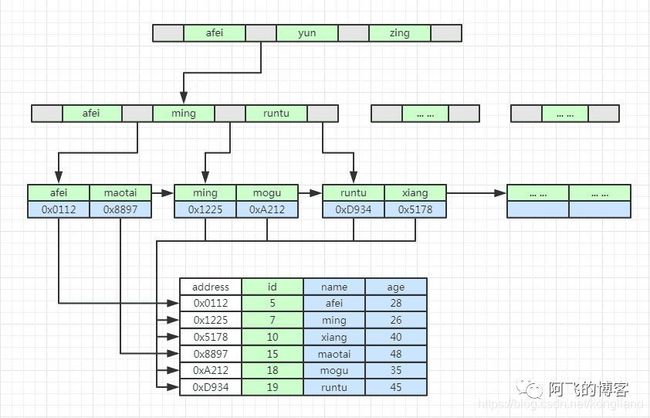
InnoDB主键索引示意图如下，非叶子节点上没有实际的数据，只有叶子节点上才有实际的数据，并且叶子节点之间有指针串联指向下一个叶子节点，这样能够提升范围查询的效率：

InnoDB B+Tree主键索引示意图

InnoDB使用了聚簇索引（Clustered），即所有二级索引聚集在主键索引上，对InnoDB存储引擎表的任何访问，最终一定要搜索主键索引树，二级索引的示意图如下：

 

 

InnoDB B+Tree二级索引示意图

在InnoDB中，二级索引（所有不是主键索引的索引）上没有实际的数据，取而代之的是主键索引的值。这样的话，如果是基于二级索引的查询，会先在二级索引上搜索得到主键索引的值，然后再去主键索引树上搜索，得到最终的行数据。

这就意味着，至少有一次索引查找，可能会有两次索引查找，其中一定有一次主键索引查找。

所以，在InnoDB中，主键要设计的尽量小，主键越小，二级索引也会越小。满足需求的情况下，SMALLINT优先于INT，INT优先于BITINT，INTEGER类型优先于VARCHAR类型。如果主键用更大的数据类型，由于二级索引上有主键索引的值，那么不只是主键索引树变的更大更高，其他的二级索引树也会更大更高，这绝对是一个糟糕的做法。

MyISAM

MyISAM没有使用聚簇索引，所以主键就是一个普通的唯一索引，并且基于索引查询只会搜索当前索引，不会和其他索引有任何关系，任意两个索引之间互不影响。如下图所示，是MyISAM的主键索引示意图，我们可以看到，索引树的叶子节点上只有表中行数据的地址，而不是和InnoDB一样，有实际的数据：

 

MyISAM的主键索引示意图

如下图所示，是MyISAM的二级索引示意图，我们可以看到，其结构几乎和主键索引示意图一样，叶子结点上也有表中行数据的地址：

 

MyISAM的二级索引示意图

B+TREE高度

了解B+Tree索引的大概结构后，我们接下来讲解一下如何计算索引树的高度。

我们先做如下假设：

表的记录数是N；

每个BTREE节点平均有B个索引KEY（即1,2,3,4,5… …）；

很明显，这时候B+TREE索引树的高度就是logBN（等价于logB/logN）。需要说明的是，这里的对数以及接下来有对数的地方应该是下图中的对数，笔者不知道如何将word中的对数复制过来，所以请将就一下下（尴尬￣□￣）：

对数

另外我们知道，由于索引树每个节点大小固定，所以索引KEY越小，B值就越大，即每个BTREE节点上可以保存更多的索引KEY。并且索引树的高度是logBN，那么B值越大，索引树的高度越小，那么基于索引查询的性能就越高。所以我们可以得到结论：相同表记录数的情况下，索引KEY越小，索引树高度就越小。

现在，我们假设表有1600w条记录（因为2^24≈1600w，便于接下来的计算），如果每个节点保存64个索引KEY，那么索引高度就是 (log10^7)/log64 ≈ 24/6 = 4。

所以，由上面的演算可知，我们要计算一张表的索引树的高度，还只需要知道一个节点有多大，从而就能知道每个节点能存储多少个索引KEY。现代数据库经过不断的探索和优化，并结合磁盘的预读特点，每个索引节点一般都是操作系统页的整数倍，操作系统页可通过命令得到该值得大小，且一般是4094，即4k。而InnoDB的pageSize可以通过命令得到，默认值是16k。

关于预读：在索引树上查到某个KEY（例如id=3），需要先找到这个KEY所在的叶子节点（因为B+Tree索引只有叶子节点上有具体的数据），这个查找过程从根节点到叶子节点，需要经过整个树。当找到叶子节点后，会根据预读原理将整个节点数据全部加载到内存中，然后基于二分法找到最终的KEY。

OK，到这里，我们距离真正计算一个拥有1600w数据的表的索引树的高度，只差每个索引KEY所占空间了。

以BIGINT为例，存储大小为8个字节。INT存储大小为4个字节（32位）。索引树上每个节点除了存储KEY，还需要存储指针。所以每个节点保存的KEY的数量为pagesize/(keysize+pointsize)（如果是B-TREE索引结构，则是pagesize/(keysize+datasize+pointsize)）。

假设平均指针大小是4个字节，那么索引树的每个节点可以存储16k/((8+4)*8)≈171。那么：一个拥有1600w数据，且主键是BIGINT类型的表的主键索引树的高度就是(log10^7)/log171 ≈ 24/7.4 ≈ 3.2。

假设平均指针大小是6个字节，那么索引树的每个节点可以存储16k/((8+6)*8)≈146。那么：一个拥有1600w数据，且主键是BIGINT类型的表的主键索引树的高度就是(log10^7)/log146 ≈ 24/7.2 ≈ 3.3。

假设平均指针大小是8个字节，那么索引树的每个节点可以存储16k/((8+8)*8)≈128。那么：一个拥有1600w数据，且主键是BIGINT类型的表的主键索引树的高度就是(log10^7)/log128 ≈ 24/7 ≈ 3.4。

由上面的计算可知：一个千万量级，且存储引擎是MyISAM或者InnoDB的表，其索引树的高度在3~5之间。

说明：这一段对索引树高度的计算，都是基于B+Tree，即InnoDB和MyISAM存储引擎的索引用到的数据结构。而B-TREE索引节点上不仅保存了索引和指针，还保存了具体的行数据，索引树的高度算法略有不同。

 

 

总结

索引树的高度是一个非常重要的东西，因为当查找的条件能用到索引时，就不用全表扫描，而是只需要在索引上搜索，从索引的根节点到叶子节点。并且很明显的是：索引树越高，性能就会越差。我们假设在最糟糕的情况下，索引一点没有被加载到内存中，而是全部持久化在磁盘上。那么索引树有多高，就表示查询至少需要多少次IO操作。即使实际情况中，由于表的数据更多，索引也会很大，不大可能全部被保存在缓存中。而且如果是二级索引搜索，IO次数还要翻倍（二级索引搜索+主键索引搜索），这对性能是一个很大的影响。

这也是MySQL数据库使用B+Tree作为索引结构的原因：尽可能降低索引树的高度。而红黑树等其他数据结构，树的高度要深的多的多。