位操作符详解(移位操作符(左移/右移)、按位与‘&’操作符、按位或‘|’操作符、按位异或‘^’操作符)
位操作是程序设计中对位模式按位或二进制数的一元和二元操作;
在许多微处理器上,位运算与加减运算速度大致相同,但位运算的速度远快于乘法运算;
位操作符的使用,可以使我们在处理一些问题上方便许多。
移位操作符
<< 左移操作符
>> 右移操作符
符号移位:正数补0,负数补1,移位的范围在0~31这个范围内;正数的移位是对原码进行,负数的移位是先将原码转化为补码-1后对补码进行移位,再转换为原码。
左移操作符 <<
将二进制最左边的数去掉,在最右边补0
例如
int i = 1;
原码:
0000 0000 0000 0000 0000 0000 0000 0001
i<<1;
0000 0000 0000 0000 0000 0000 0000 0010
最终i = 2右移操作符>>
将二进制最右边的数去掉,若该数为负数,左边补1,若该数为正数,左边补0
例如
int i = -10;
原码:1000 0000 0000 0000 0000 0000 0000 1010
反码:1111 1111 1111 1111 1111 1111 1111 0101
补码:1111 1111 1111 1111 1111 1111 1111 0110
i>>2
补码:1111 1111 1111 1111 1111 1111 1111 1101
原码:1000 0000 0000 0000 0000 0000 0000 1100
则右移两位后i = -3位操作符
& //按位与
| //按位或
^ //按位异或
注意:位操作符的操作数必须为整数
按位与‘&’:两个二进制序列同一位上都为1则为1,否则为0;
按位或‘|’:两个二进制序列同一位上有1则为1,否则为0;
按位异或‘^’:两个二进制序列同一位上的数字相同则为0,不同则为1.
以下列程序设计题为例,来深刻理解按位操作符的性质
1.两个int(32位)整数m和n的二进制表达中,有多少个位(bit)不同?
输入样例:
1999 2299
输出样例:7
思路:
1. 先将m和n进行按位异或,此时m和n相同的二进制比特位清零,不同的二进制比特位为1;
2.统计异或完成后结果的二进制比特位中有多少个1.
代码如下:
#include
int main()
{
int m, n, count = 0;
scanf("%d %d", &m, &n);
int tmp = m ^ n;
while (tmp)
{
tmp = tmp & (tmp - 1);
count++;
}
printf("%d", count);
return 0;
} 运行结果:
2.打印整数二进制的奇数位和偶数位
思路:
1.提取所有的奇数位,如果该位是1,输出1,是0则输出0;
2.以同样的方式提取偶数位置.
#include
int main()
{
int m;
scanf("%d", &m);
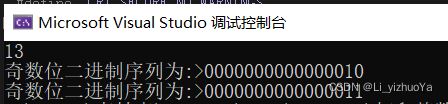
printf("奇数位二进制序列为:>");
for (int i = 31; i > 0; i -= 2)
printf("%d", (m >> i) & 1);
printf("\n奇数位二进制序列为:>");
for (int i = 30; i >= 0; i -= 2)
printf("%d", (m >> i) & 1);
return 0;
} 该题是按位运算与移位运算两种方法的结合。
运行结果:
3.不允许创建临时变量,交换两个整数的内容
解题思路:
以m = 12, n = 13为例
m = 12的二进制序列:
0000 0000 0000 0000 0000 0000 0000 1100 m=12
n = 13的二进制序列:
0000 0000 0000 0000 0000 0000 0000 1101 n=13
m = m ^ n;
0000 0000 0000 0000 0000 0000 0000 0001 m=1
n = m ^ n;
0000 0000 0000 0000 0000 0000 0000 1100 n=12
m = m ^ n;
0000 0000 0000 0000 0000 0000 0000 1101 m=13
代码如下:
#include
int main()
{
int m, n;
scanf("%d %d", &m, &n);
m = m ^ n;
n = m ^ n;
m = m ^ n;
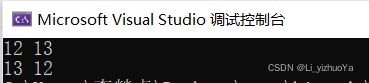
printf("%d %d", m, n);
return 0;
} 运行结果:
4.统计二进制中1的个数
写一个函数返回参数二进制中 1 的个数。
比如: 15 0000 1111 4 个 1
代码如下:
#include
int count_one_bit(int n);//方法一
int count_one_bit1(int n);//方法二
int count_one_bit2(int n);//方法三
int main()
{
int n, count = 0;
scanf("%d", &n);
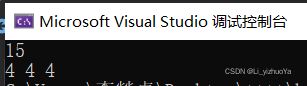
printf("%d %d %d", count_one_bit(n), count_one_bit1(n), count_one_bit2(n));
return 0;
}
int count_one_bit(int n)
{
int count = 0;
while (n)
{
if (n % 2 == 1)
count++;
n = n / 2;
}
return count;
}
int count_one_bit1(int n)
{
int count = 0;
for (int i = 0; i < 32; i++)
{
if ((n >> i) & 1 == 1)
count++;
}
return count;
}
int count_one_bit2(int n)
{
int count = 0;
while (n)
{
n = n & (n - 1);
count++;
}
return count;
} 运行结果:
当输入的数字为正数时,三种方法都可以得到正确的结果,但当输入的数字为负数时,方法一不能得到正确的输出结果,说明该方法不能进行负数的位运算。
方法二是对于方法一的改进
其优点为:用位操作代替取模和除法运算,效率稍微比较高;
其缺点为:不论是什么数据,循环都要执行32次.
方法三是对于方法二的改进
其思路为采用相邻的两个数据进行按位与运算,根据观察,此种方式,数据的二进制比特位中有几个1,循环就循环几次,而且中间采用了位运算,处理起来比较高效。