力扣面试经典150题(二)
55
55. 跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
class Solution {//从后往前遍历观察能否到达设定的tar
public boolean canJump(int[] nums) {
int len = nums.length;
if (len == 1) {
return true;
}
int tar=len-1;
for(int i=len-2;i>=0;i--){
if(i+nums[i]>=tar){
tar=i;
}
}
if(tar==0){
return true;
}
return false;
}
}45
45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
class Solution {
public int jump(int[] nums) {
int max=0;
int c=0;
int min=0;
int len = nums.length;
if(len ==1){
return min;
}
for(int i=0;i<=c;i++){
if(i+nums[i]>c&&i+nums[i]>max){
max = i+nums[i];
if(max>=len-1){
min++;
return min;
}
}
if(c==i){
c=max;
min++;
}
}
return min;
}
}
/** 首先定义了三个变量maxCover、cover和minStep,分别表示最大覆盖值、当前覆盖值和最小步数。
然后通过一个for循环遍历数组nums,在循环中判断当前位置i加上nums[i]能否更新maxCover的值。如果能更新maxCover,则判断maxCover是否已经能够覆盖到数组的最后一个位置,如果能够覆盖到最后一个位置,则说明已经找到了最小步数,直接返回minStep。
如果无法更新maxCover,则判断当前位置i是否等于cover,如果等于则说明需要更新搜索范围,将cover更新为maxCover,并且步数加一。
最后返回minStep即为最小步数。*/274
274. H 指数
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值,h 指数 是其中最大的那个。
class Solution {
public int hIndex(int[] citations) {
int len = citations.length;
int l = len+1;
int []h = new int[l];
for(int i=1;i<=len;i++){
for(int j=0;j=i){
h[i]++;
}
}
}
for(int i = len;i>0;i--){
if(h[i]>=i){
return i;
}
}
return 0;
}
} 380
380. O(1) 时间插入、删除和获取随机元素
实现RandomizedSet 类:
RandomizedSet()初始化RandomizedSet对象bool insert(int val)当元素val不存在时,向集合中插入该项,并返回true;否则,返回false。bool remove(int val)当元素val存在时,从集合中移除该项,并返回true;否则,返回false。int getRandom()随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素)。每个元素应该有 相同的概率 被返回。
你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1) 。
import java.util.*;
class RandomizedSet {
List list = new ArrayList<>();
public RandomizedSet() {
boolean insert;
boolean remove;
int getRandom;
}
public boolean insert(int val) {
for(int i=0;i 238
238. 除自身以外数组的乘积
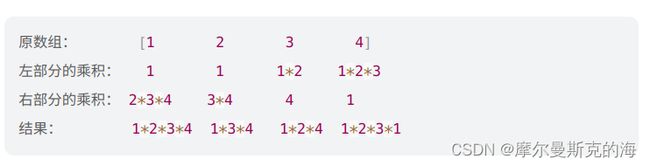
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
左乘积和右乘积
class Solution {
public int[] productExceptSelf(int[] nums) {
int len = nums.length;
int [] left = new int[len];
int [] right = new int[len];
int count=1;
int p =len-1;
left[0] = 1;
right[p]=1;
for(int i=1;i=0;i--){//p是数组最后一个元素编号,p-1是倒数第二个
count *= nums[i+1];
right[i] = count;
}
int []result = new int[len];
for(int i=0;i 134
134. 加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int len = gas.length;
int count =0;
int sum=0;
int flag=0;
for(int i=0;i=0){
return flag;
}else{
return -1;
}
}
} 135
135. 分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
class Solution {
public int candy(int[] ratings) {
int len = ratings.length;
int[] candies = new int[len];
int count = 0;
for (int i = 0; i < len; i++) {
candies[i] = 1;
}
for (int i = 1; i < len; i++) {
if (ratings[i] > ratings[i - 1]) {
candies[i] = candies[i - 1] + 1;
}
}
for (int i = len - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candies[i] = Math.max(candies[i], candies[i + 1] + 1);
}
}
for (int i = 0; i < len; i++) {
count += candies[i];
}
return count;
}
}
//可能本身的糖果数就大于相邻的糖果数42
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
class Solution {//首先记住第一个和最后一个柱子不接雨水
public int trap(int[] height) {
int len = height.length;
int count = 0;
int[] leftMax = new int[len];
int[] rightMax = new int[len];
//柱子接的雨水的数量为左边柱子最高和右边柱子最高的差
leftMax[0] = height[0];
for (int i = 1; i < len; i++) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
rightMax[len - 1] = height[len - 1];
for (int i = len - 2; i >= 0; i--) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
//使用双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。
//把每一个位置的左边最高高度记录在一个数组上(maxLeft),
//右边最高高度记录在一个数组上(maxRight),这样就避免了重复计算。
for (int i = 1; i < len - 1; i++) {
int minHeight = Math.min(leftMax[i], rightMax[i]);
count += minHeight - height[i];
}
return count;
}
}