CDQ分治处理多维偏序基础

CDQ分治是一种离线处理多维偏序问题的算法框架。它不是一个具体的算法，但是为多维偏序问题提供了一个框架结构。以下首先介绍多维偏序问题的CDQ分治框架，从低维到高维；然后介绍几个简单的可以被抽象为多维偏序的修改查询操作的问题。

多维偏序问题

要想使用CDQ分治解决多维偏序问题，首先还是要从基础的逆序对问题说起，然后再到高维。

逆序对的两种解法

逆序对就是一个典型的偏序问题。当$i<j且A_i>A_j$时，对答案有影响。因此是一个二维偏序问题。不过，由于$i,j$天然有序，有时候也可以看作是一个“一维偏序”问题。总之逆序对是分治的基础问题。CDQ分治的基本思路和算法框架在逆序对问题中已经有了完整的体现，剩下的只是细节问题。
逆序对的另外一种解法——使用树状数组，也是CDQ分治在处理多维偏序中经常使用的技术。因此，逆序对问题是CDQ分治的入门门槛。

逆序对的分治解法

LuoguP1908逆序对模板题

#include 
using namespace std;

int getInt(){
	int sgn = 1;
	char ch = getchar();
	while( ch != '-' && ( ch < '0' || ch > '9' ) ) ch = getchar();
	if ( '-' == ch ) {sgn = 0;ch=getchar();}

	int ret = (int)(ch-'0');
	while( '0' <= (ch=getchar()) && ch <= '9' ) ret = ret * 10 + (int)(ch-'0');
	return sgn ? ret : -ret;
}

int N;
int A[1000100];
int B[1000100];
long long int Ans = 0;

void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s+e) >> 1;
    CDQ(s, mid); CDQ(mid+1, e);

    int a = s, b = mid + 1, t = s;
    while(a<=mid&&b<=e){
        if(A[a]<=A[b]){
            B[t++] = A[a++];
        }else{
            Ans += mid - a + 1;
            B[t++] = A[b++];
        }
    }
    while(a<=mid){
        B[t++] = A[a++];
    }
    while(b<=e){
        B[t++] = A[b++];
    }
    copy(B+s, B+e+1, A+s);
}

int main(){
    //freopen("1.txt","r",stdin);
    N = getInt();
    for(int i=1;i<=N;++i) A[i] = getInt();

    Ans = 0;
    CDQ(1, N);
    printf("%lld\n",Ans);
    return 0;
}

这个分治解法已经包括了CDQ分治的主框架。首先，CDQ函数是一个递归函数，最开始是递归结束条件以及递归。其后就是一个归并过程。在归并过程中，实现对答案的统计。

void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s+e) >> 1;
    CDQ(s, mid); CDQ(mid+1, e);

    int a = s, b = mid + 1, t = s;
    while(a<=mid&&b<=e){
        if(A[a]<=A[b]){
            /*do something needed*/
            B[t++] = A[a++];
        }else{
            /*do something needed*/
            B[t++] = A[b++];
        }
    }
    while(a<=mid){
        /*do something needed*/
        B[t++] = A[a++];
    }
    while(b<=e){
        /*do something needed*/
        B[t++] = A[b++];
    }
    copy(B+s, B+e+1, A+s);
}

考虑单独一次的CDQ调用，在进入归并之前，已经有了左右两段，且左右两段的值分别有序（这其实就是第二维），同时左边段的索引均小于右边段的索引（这其实就是第一维），同时左右两段内部各自的答案已经统计完了。如下图所示。
现在要做的事情就是统计由左右两段之间产生的答案，同时统计完毕以后，使得整段值有序（这其实就是由归并完成的）。
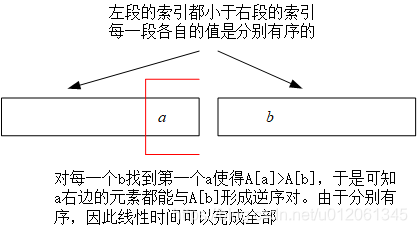统计答案就得依赖于具体的问题了。这里统计的是逆序对。因此对右边段的每一个$A_b$，在左边找到第一个$a$使得$A_a>A_b$，这样的话$a$及$a$右边的数都能与$A_b$形成逆序对，于是可以加上。另一方面，由于两段分别有序，因此这个过程只需要线性时间就可以全部完成。

逆序对的树状数组解法

同样是LuoguP1908逆序对模板题，采用树状数组的做法可以看这里。这里有一个小技术——离散化，在这类问题中是经常用到的。这里主要体现的思想是：树状数组可以抵掉一维CDQ分治。因此，在后面的高维偏序中，可以有CDQ套CDQ的做法，也可以有CDQ套树状数组的做法。

二维偏序的解法

二维偏序的分治解法

如果对逆序对的分治解法很清楚的话，普通二维偏序解法只是多了一个排序而已，对第一维排序。
譬如POJ2352，给定坐标，本质上是问左下方的点有多少个。因此就是当$x_i\le x_j$且$y_i\le y_j$时对答案有贡献，典型的二维偏序。当然，由于这道题本身按$y$的升序给出，所以就不用排序了。并且要$x$当做第二维。另外这一道题不是统计一个全局的答案，而是对每个点单独统计，所以前面写一个结构体比较方便一点。

#include 
#include 
using namespace std;

char *__abc147, *__xyz258, __ma369[100000];
#define __hv007() ((__abc147==__xyz258) && (__xyz258=(__abc147=__ma369)+fread(__ma369,1,100000,stdin),__abc147==__xyz258) ? EOF : *__abc147++)

int getInt(){
	int sgn = 1;
	char ch = __hv007();
	while( ch != '-' && ( ch < '0' || ch > '9' ) ) ch = __hv007();
	if ( '-' == ch ) {sgn = 0;ch=__hv007();}

	int ret = (int)(ch-'0');
	while( '0' <= (ch=__hv007()) && ch <= '9' ) ret = ret * 10 + (int)(ch-'0');
	return sgn ? ret : -ret;
}

int const SIZE = 15010;
typedef long long llt;

struct cdq_t{
    int x;
    int y;
    int *pans;
}A[SIZE], B[SIZE];

int N;
int Ans[SIZE], Level[SIZE];

void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s+e)>>1;
    CDQ(s, mid);CDQ(mid+1, e);

    int a = s, b = mid+1, t = s, sum = 0;
    while(a<=mid && b<=e){
        if(A[a].x<=A[b].x){
            B[t++] = A[a++];
        }else{
            *A[b].pans += a - s;
            B[t++] = A[b++];
        }
    }
    while(a<=mid){
        B[t++] = A[a++];
    }
    while(b<=e){
        *A[b].pans += a - s;
        B[t++] = A[b++];
    }
    copy(B+s, B+e+1, A+s);
}

int main(){
    //freopen("1.txt","r",stdin);
    N = getInt();
    for(int i=1;i<=N;++i){
        A[i].x = getInt();
        A[i].y = getInt();
        *(A[i].pans = Ans + i) = 0;
    }

    CDQ(1, N);
    for(int i=1;i<=N;++i)++Level[Ans[i]];
    for(int i=0;i<N;++i)printf("%d\n", Level[i]);
    return 0;
}

CDQ函数的主体结构与逆序对问题中其实并无区别，就是一个归并过程。在归并之前同样有左右两段，其中左边段的$y$坐标均要小于右边段，左右两段内部各自的$x$坐标分别有序。在归并过程中，对右边段的每一个$b$，在左边段找到第一个$a$满足大于$x_a>x_b$，这样，$a$左边的元素的$x$坐标均小于等于$b$的，而且已知$y$坐标肯定小，因此这部分对$b$的答案都有贡献，记录下来。同样，由于两段分别有序，因此在线性时间内可以完成全部过程。
归并完成之后，就得到了左右两段之间对答案的贡献，同时这一整段变成了第二维有序。

二维偏序的树状数组解法

POJ2481，给定N个区间$[s,e]$。 如果$a$区间能够真包含$b$区间，则称$a$比$b$强壮。对每一个区间，问比其强壮的区间有多少个。显然当$s_i\le s_j$且$e_i\ge e_j$时（因为是真包含，要排除掉完全相等，可以去重，也可以统计的时候再考虑），对答案有影响，二维偏序问题。树状数组的做法可以看这里。可以看到树状数组充当了一层CDQ。首先仍然是要排序，第一维有序，然后对第二维进行统计。

三维偏序的解法

对二维偏序总结下来就是：第一维排序，第二维CDQ或者树状数组。现在又加了一维，因此有两种做法：第一维排序，第二维CDQ，第三维CDQ或者树状数组。当然，还有树套树、$KDTree$等做法，这里只说CDQ分治下的做法。

三维偏序的分治套分治解法

首先仍然回到二维偏序问题，假设对每个$i$要统计$x_j<x_i$且$y_j<y_i$。考虑每一次归并的过程，归并之前有左右两段，左段的$x$坐标均小于右段，每一段内部$x$坐标是无序的，每一段内部的$y$坐标是有序的，每一段内部对答案的贡献已经统计完毕。

经过归并形成了一整段，整段$y$坐标有序，而$x$坐标无序，且左右两段之间对答案的贡献均以统计完毕。
现在考虑第三维的分治归并，跟二维归并过程类似，在第三维分治的时候，对右段的每个点可以找到左段的$y,z$坐标均小的点，现在唯一的问题是$x$坐标怎么办？

这个问题在第二维归并的时候解决，在第二维归并的时候，可以设置一个标志位，这样在第三维归并的时候，就可以知道这个点是来自于第二维的左段还是右段。在第三维归并统计答案的时候，要求$b$来自于第二维的右段，而对它有贡献的点必须来自第二维左段。因为如果$b$来自于第二维的左段，那么这两段之间不可能对它的答案有贡献。而对$b$有贡献的点，如果不是来自于第二维左段，是来自于右段，那么它在之前就已经统计过了，无需在这里统计。

洛谷3810三维偏序模板题，CDQ套CDQ的做法。

#include 
using namespace std;

int const SIZE = 120000;

int N,K;
int Ans[SIZE]={0};
int Cnt[SIZE]={0};

struct cdq_t{
    int x,y,z;
    bool b;
    int *ans;
    inline void get(){
        scanf("%d%d%d",&x,&y,&z);
        return;
    }
    bool operator==(const cdq_t &rhs)const{
        return x==rhs.x&&y==rhs.y&&z==rhs.z;
    }
    bool operator < (const cdq_t &rhs)const{
        if(x!=rhs.x) return x < rhs.x;
        if(y!=rhs.y) return y < rhs.y;
        return z < rhs.z;
    }
}A[SIZE],B[SIZE],C[SIZE];


void CDQ2(int s,int e){
    if(s==e)return;

    int mid=(s+e)>>1;
    CDQ2(s,mid);CDQ2(mid+1,e);

    int a=s,b=mid+1,t=s,cnt=0;
    while(a<=mid&&b<=e){
        if(B[a].z<=B[b].z){
            cnt += B[a].b;
            C[t++] = B[a++];
        }else{
            if(!B[b].b) *B[b].ans += cnt;
            C[t++] = B[b++];
        }
    }
    while(a<=mid){
        //cnt += B[a].b;
        C[t++] = B[a++];
    }
    while(b<=e){
        if(!B[b].b) *B[b].ans += cnt;
        C[t++] = B[b++];
    }
    copy(C+s,C+e+1,B+s);
}

void CDQ(int s,int e){
    if(s==e)return;
    int mid=(s+e)>>1;
    CDQ(s,mid);CDQ(mid+1,e);

    int a=s, b=mid+1, t=s;
    while(a<=mid&&b<=e){
        if(A[a].y<=A[b].y){
            B[t] = A[a++];
            B[t++].b = 1;
        }else{
            B[t] = A[b++];
            B[t++].b = 0;
        }
    }
    while(a<=mid){
        B[t] = A[a++];
        B[t++].b = 1;
    }
    while(b<=e){
        B[t] = A[b++];
        B[t++].b = 0;
    }
    copy(B+s, B+e+1, A+s);
    CDQ2(s,e);
}

int main(){
    scanf("%d%d",&N,&K);
    for(int i=1;i<=N;++i){
        A[i].get(),A[i].ans=&Ans[i],Ans[i]=0;
    }

    sort(A+1,A+N+1);
    for(int i=N-1;i;--i){
        if(A[i]==A[i+1]){
            *A[i].ans=*A[i+1].ans+1;
        }
    }


    CDQ(1,N);
    for(int i=1;i<=N;++i)++Cnt[Ans[i]];
    for(int i=0;i<N;++i)printf("%d\n",Cnt[i]);
    return 0;
}

三维偏序的CDQ套树状数组的解法

相较而言，CDQ套树状数组应该更容易理解。在归并第二维的过程中，要考虑第三维的影响。如下图所示，现在已经找到了两个维度符合条件的点，只需要在这里面筛选第三维坐标即可。如果前面用树状数组解决了逆序对和二维偏序的问题，这里很容易套用上树状数组。当然用树状数组，可能需要用到离散化。

#include 
#include 
using namespace std;

char *__abc147, *__xyz258, __ma369[100000];
#define __hv007() ((__abc147==__xyz258) && (__xyz258=(__abc147=__ma369)+fread(__ma369,1,100000,stdin),__abc147==__xyz258) ? EOF : *__abc147++)

int getInt(){
	int sgn = 1;
	char ch = __hv007();
	while( ch != '-' && ( ch < '0' || ch > '9' ) ) ch = __hv007();
	if ( '-' == ch ) {sgn = 0;ch=__hv007();}

	int ret = (int)(ch-'0');
	while( '0' <= (ch=__hv007()) && ch <= '9' ) ret = ret * 10 + (int)(ch-'0');
	return sgn ? ret : -ret;
}

int const SIZE = 100030;
typedef long long llt;

inline int lowbit(int x){return x&-x;}

struct cdq_t{
    int idx;
    int x;
    int y;
    int z;
    int cnt;
    bool operator < (const cdq_t&rhs)const{
        return this->x < rhs.x || (this->x==rhs.x&&this->y<rhs.y)
            || (this->x==rhs.x&&this->y==rhs.y&&this->z<rhs.z)
            || (this->x==rhs.x&&this->y==rhs.y&&this->z==rhs.z&&this->idx<rhs.idx);
    }
}A[SIZE], B[SIZE];

int N, Q, K;
int C[SIZE+SIZE];
int Ans[SIZE];

int query(int pos){
    int ans = 0;
    for(;pos;pos-=lowbit(pos))ans+=C[pos];
    return ans;
}

void modify(int pos, int delta){
    for(;pos<=K;pos+=lowbit(pos)) C[pos] += delta;
}

void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s+e) >> 1;
    CDQ(s, mid); CDQ(mid+1, e);

    int a = s, b = mid+1, t = s;
    while(a<=mid&&b<=e){
        if(A[a].y<=A[b].y){
            modify(A[a].z, A[a].cnt);
            B[t++] = A[a++];
        }else{
            Ans[A[b].idx] += query(A[b].z);
            B[t++] = A[b++];
        }
    }
    while(a<=mid){
        modify(A[a].z, A[a].cnt);
        B[t++] = A[a++];
    }
    while(b<=e){
        Ans[A[b].idx] += query(A[b].z);
        B[t++] = A[b++];
    }

    /// 清空树状数组，但是不能直接fill
    for(int i=s;i<=mid;++i){
        modify(A[i].z, -A[i].cnt);
    }

    copy(B+s, B+e+1, A+s);
}

int Cnt[SIZE];
int main(){
    //freopen("1.txt","r",stdin);
    N = getInt();
    K = getInt();
    for(int i=1;i<=N;++i){
        A[A[i].idx = i].x = getInt();
        A[i].y = getInt();
        A[i].z = getInt();
        A[i].cnt = 0;
    }
    sort(A+1, A+N+1);
    Q = 0;
    for(int i=1;i<=N;++i){
        if(Q && A[Q].x==A[i].x&&A[Q].y==A[i].y&&A[Q].z==A[i].z){
            ++A[Q].cnt;
        }else{
            A[++Q] = A[i];
            A[A[Q].idx = Q].cnt = 1;
        }
    }
    CDQ(1, Q);
    for(int i=1;i<=Q;++i)Ans[A[i].idx] += A[i].cnt - 1;
    for(int i=1;i<=Q;++i)Cnt[Ans[A[i].idx]] += A[i].cnt;
    for(int i=0;i<N;++i)printf("%d\n", Cnt[i]);
    return 0;
}

CDQ处理查询操作相关问题

CDQ处理相关操作问题，首先要抽象成多维偏序问题。

CDQ分治解决树状数组

考虑洛谷3374，这其实是一个树状数组的题目。要求2种操作：

1. x k: 第x个位置加上k
2. x y: 求[x, y]区间和

首先将操作修改一下，改为：

1. x k: 第x个位置加上k
2. x: 求[1, x]的区间和

显然，当$T_i<T_j$且$X_i<X_j$且操作$i$是增加而操作$j$是查询时，对答案有影响。其中$T$指操作的序数，可以视为操作发生的时间。尽管多了点条件，但是显然可以在多维偏序中统计答案。至于区间求和，稍微考虑一下就可以解决。

#include 
using namespace std;

char *__abc147, *__xyz258, __ma369[100000];
#define __hv007() ((__abc147==__xyz258) && (__xyz258=(__abc147=__ma369)+fread(__ma369,1,100000,stdin),__abc147==__xyz258) ? EOF : *__abc147++)

int getInt(){
	int sgn = 1;
	char ch = __hv007();
	while( ch != '-' && ( ch < '0' || ch > '9' ) ) ch = __hv007();
	if ( '-' == ch ) {sgn = 0;ch=__hv007();}

	int ret = (int)(ch-'0');
	while( '0' <= (ch=__hv007()) && ch <= '9' ) ret = ret * 10 + (int)(ch-'0');
	return sgn ? ret : -ret;
}

int const SIZE = 500010;
typedef long long llt;

struct cdq_t{
    int type; // 124
    int pos;
    int val;
    cdq_t(int a=0,int b=0,int c=0):type(a),pos(b),val(c){}
}A[SIZE*3], B[SIZE*3];

int N, M, Q, ACnt;
int Ans[SIZE];
void disp(int,int);
void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s+e)>>1;
    CDQ(s, mid);
    CDQ(mid+1, e);

    int a = s, b = mid+1, t = s, sum = 0;
    while(a<=mid && b<=e){
        if(A[a].pos <= A[b].pos){ // 说明a位置在b位置左边
            if(A[a].type&1){ // 修改操作
                sum += A[a].val;
            }
            B[t++] = A[a++];
        }else{ // 说明a位置在b位置右边
            if(A[b].type&2){
                Ans[A[b].val] -= sum;
            }else if(A[b].type&4){
                Ans[A[b].val] += sum;
            }
            B[t++] = A[b++];
        }
    }
    /// 如果a还有剩余，就无所谓了
    while(a<=mid) B[t++] = A[a++];
    /// 右边还有剩余，还需考虑
    while(b<=e){
        if(A[b].type&2){
            Ans[A[b].val] -= sum;
        }else if(A[b].type&4){
            Ans[A[b].val] += sum;
        }
        B[t++] = A[b++];
    }
    /// 将其按照位置变得有序
    copy(B+s, B+e+1, A+s);
    //disp(s, e);
}

void disp(int s, int e){
    printf("[%d, %d]\n", s, e);
    for(int i=s;i<=e;++i){
        printf("%d: %d %d %d\n", i, A[i].type, A[i].pos, A[i].val);
    }
    for(int i=1;i<=ACnt;++i){
        printf("%d: %d\n", i, Ans[i]);
    }
}
int main(){
    //freopen("1.txt","r",stdin);
    N = getInt();
    M = getInt();
    for(int i=1;i<=N;++i){
        A[i] = cdq_t(1, i, getInt());
    }

    Q = N; ACnt = 0;
    for(int i=0;i<M;++i){
        if((A[++Q].type = getInt())&1){
            A[Q].pos = getInt();
            A[Q].val = getInt();
        }else{
            A[Q].pos = getInt() - 1;
            A[Q].val = ++ACnt;

            A[++Q].type = 4;
            A[Q].pos = getInt();
            A[Q].val = ACnt;
        }
    }

    CDQ(1, Q);
    for(int i=1;i<=ACnt;++i)printf("%d\n", Ans[i]);
    return 0;
}

CDQ分治解决动态逆序对

考虑洛谷3157动态逆序对，将时间轴反过来，把删除数字看作是插入数字，则当$T_i<T_j$且$P_i<P_j$且$V_i>V_j$，对答案有影响；同时当$T_i<T_j$且$P_i>P_j$且$V_i<V_j$，也对答案有影响。因此是两个三维偏序问题。既然是三维偏序，可以用CDQ套CDQ，也可以用CDQ套树状数组。相对而言，套树状数组应该要简单易实现一些。这里用了CDQ套CDQ的方法。由于要在一个程序中解决两个三维偏序问题，因此实际上写了两套CDQ，但是共享一个框架，根据$flag$参数决定具体走向。

#include 
using namespace std;

char *__abc147, *__xyz258, __ma369[100000];
#define __hv007() ((__abc147==__xyz258) && (__xyz258=(__abc147=__ma369)+fread(__ma369,1,100000,stdin),__abc147==__xyz258) ? EOF : *__abc147++)

int getUnsigned(){
	char ch = __hv007();
	while( ch < '0' || ch > '9' ) ch = __hv007();

	int ret = (int)(ch-'0');
	while( '0' <= ( ch = __hv007() ) && ch <= '9' ) ret = (ret<<1) + (ret<<3) + (int)(ch-'0');
	return ret;
}

typedef long long llt;
int const SIZE = 120000;

int N, M;
llt Ans[SIZE]={0};

struct cdq_t{
    int time;
    int pos;
    int val;
    int b;
}A[SIZE],B[SIZE],C[SIZE];

bool operator < (const cdq_t&lhs, const cdq_t&rhs){
    if(lhs.time!=rhs.time) return lhs.time < rhs.time;
    if(lhs.pos!=rhs.pos) return lhs.pos < rhs.pos;
    return lhs.val < rhs.val;
}


void CDQ2(int s,int e,int flag){
    if(s==e)return;

    int mid=(s+e)>>1;
    CDQ2(s,mid,flag);CDQ2(mid+1,e,flag);

    int a=s,b=mid+1,t=s,cnt=0;
    while(a<=mid&&b<=e){
        if(flag&1){
            if(B[a].val>B[b].val){
                cnt += B[a].b;
                C[t++] = B[a++];
            }else{
                if(!B[b].b) Ans[B[b].time] += cnt;
                C[t++] = B[b++];
            }
        }else{
            if(B[a].val<B[b].val){
                cnt += B[a].b;
                C[t++] = B[a++];
            }else{
                if(!B[b].b) Ans[B[b].time] += cnt;
                C[t++] = B[b++];
            }
        }
    }
    while(a<=mid){
        cnt += B[a].b;
        C[t++] = B[a++];
    }
    while(b<=e){
        if(!B[b].b) Ans[B[b].time] += cnt;
        C[t++] = B[b++];
    }
    copy(C+s,C+e+1,B+s);
}

///flag为1时统计pos小但val大的
///flag为2时统计pos大但val小的
void CDQ(int s,int e,int flag){
    if(s==e)return;
    int mid=(s+e)>>1;
    CDQ(s,mid,flag);CDQ(mid+1,e,flag);

    int a=s, b=mid+1, t=s;
    while(a<=mid&&b<=e){
        if(flag&1){
            if(A[a].pos<=A[b].pos){
                B[t] = A[a++];
                B[t++].b = 1;
            }else{
                B[t] = A[b++];
                B[t++].b = 0;
            }
        }else{
            if(A[a].pos>A[b].pos){
                B[t] = A[a++];
                B[t++].b = 1;
            }else{
                B[t] = A[b++];
                B[t++].b = 0;
            }
        }
    }
    while(a<=mid){
        B[t] = A[a++];
        B[t++].b = 1;
    }
    while(b<=e){
        B[t] = A[b++];
        B[t++].b = 0;
    }
    copy(B+s, B+e+1, A+s);
    CDQ2(s,e,flag);
}

int Val2Pos[SIZE];
int main(){
    //freopen("1.txt","r",stdin);
    N = getUnsigned();
    M = getUnsigned();
    for(int i=1;i<=N;++i){
        A[Val2Pos[A[i].val = getUnsigned()] = A[i].pos = i].time = 1;
    }
    for(int v, i=1;i<=M;++i){
        A[Val2Pos[v = getUnsigned()]].time = M - i + 1;
    }
    sort(A, A+N+1);
    CDQ(1,N,1);

    sort(A, A+N+1);
    CDQ(1,N,2);
    for(int i=1;i<=M;++i)Ans[i] += Ans[i-1];
    for(int i=M;i>=1;--i)printf("%lld\n", Ans[i]);
    return 0;
}

2019年河北省赛I题

2019年河北省赛I题牛客26006，在二维平面上有一些星星，每个星星有一个初始亮度，然后随时间做周期性变化。到达一个固定的最大值后，又从0开始递增。有多个询问。每个询问问指定时刻的区域内的亮度总和是多少。同样，首先把询问修改一下，改为问指定时刻以$(1,1)到(x,y)$的矩形亮度总和是多少。然后把时间线反过来（最开始看错题了），以星星达到最大值时为一个插入操作。则当$T_i\le T_j,x_i\le x_j,y_i\le y_j$且$i$操作是插入而$j$操作是查询时对答案有影响。由于是周期性变化，实际上当$T_i\ge T_j,x_i\le x_j,y_i\le y_j$且$i$操作是插入而$j$操作是查询时也对答案有影响。同时，由于不是统计亮着的星星的数量，而是要统计亮度，因此$T$这一维不仅要比大小，还要比差值，因此不能放在第一维，要放在最后一维。总之是一个三维偏序问题。既然如此，就存在CDQ套CDQ以及CDQ套树状数组的做法。

CDQ套CDQ，这个做法时间有点紧，要找个没人的时候提交。否则容易T。

#pragma GCC optimize("-O2")
#include 
using namespace std;

char *__abc147, *__xyz258, __ma369[100000];
#define __hv007() ((__abc147==__xyz258) && (__xyz258=(__abc147=__ma369)+fread(__ma369,1,100000,stdin),__abc147==__xyz258) ? EOF : *__abc147++)

inline int getUnsigned(){
	char ch = __hv007();
	while( ch < '0' || ch > '9' ) ch = __hv007();

	int ret = (int)(ch-'0');
	while( '0' <= ( ch = __hv007() ) && ch <= '9' ) ret = (ret<<1) + (ret<<3) + (int)(ch-'0');
	return ret;
}

typedef long long llt;
int const SIZE = 250500;

void write(llt x){if (x<10) {putchar('0'+x); return;} write(x/10); putchar('0'+x%10);}
inline void writeln(int x){ write(x); putchar('\n'); }

llt MAX;
int N, Q, QCnt;
llt Ans[SIZE]={0};

struct cdq_t{
    int time;
    int x;
    int y;
    int op; // 操作，1表示插入，2表示询问右上角，4表示询问的另外三个角
    int b;
    llt* pans; // 记住答案的位置
}A[SIZE],B[SIZE],C[SIZE];

inline bool operator < (const cdq_t&lhs, const cdq_t&rhs){
    if(lhs.x!=rhs.x) return lhs.x < rhs.x;
    if(lhs.y!=rhs.y) return lhs.y < rhs.y;
    if(lhs.time!=rhs.time) return lhs.time < rhs.time;
    return lhs.op < rhs.op; // 如果都一样，插入操作在前
}

inline bool cmp2 (const cdq_t&lhs, const cdq_t&rhs){
    if(lhs.x!=rhs.x) return lhs.x < rhs.x;
    if(lhs.y!=rhs.y) return lhs.y < rhs.y;
    if(lhs.time!=rhs.time) return lhs.time > rhs.time;
    return lhs.op < rhs.op; // 如果都一样，插入操作在前
}

void disp(int n){
    for(int i=1;i<=n;++i){
        printf("%d: %d %d %d ", i, A[i].time, A[i].x, A[i].y);
        if(A[i].op&1) puts("insert");
        else if(A[i].op&2) puts("query");
        else if(A[i].op&4) puts("q----");
        else throw runtime_error("wrong cmd.");
    }
}

void CDQ2(int s, int e, int flag){
    if(s>=e) return;
    int mid = (s+e) >> 1;
    CDQ2(s, mid, flag); CDQ2(mid+1, e, flag);

    int a = s, b = mid+1, t = s;
    int cnt = 0;
    llt sum = 0;

    while(a<=mid&&b<=e){
        if(flag&1){
            if(B[a].time<=B[b].time){
                if(B[a].op&1){ // 修改操作
                    cnt += B[a].b;
                    sum += B[a].time * B[a].b;
                }
                C[t++] = B[a++];
            }else{
                if(!B[b].b){
                    if(B[b].op&2){ // 查询操作，正的
                        *B[b].pans += cnt * (MAX-B[b].time) + sum;
                    }else if(B[b].op&4){
                        *B[b].pans -= cnt * (MAX-B[b].time) + sum;
                    }
                }
                C[t++] = B[b++];
            }
        }else{
            if(B[a].time>B[b].time){
                if(B[a].op&1){ // 修改操作
                    cnt += B[a].b;
                    sum += B[a].time * B[a].b;
                }
                C[t++] = B[a++];
            }else{
                if(!B[b].b){
                    if(B[b].op&2){ // 查询操作，正的
                        *B[b].pans += sum - cnt * B[b].time - cnt;
                    }else if(B[b].op&4){
                        *B[b].pans -= sum - cnt * B[b].time - cnt;
                    }
                }
                C[t++] = B[b++];
            }
        }
    }
    while(a<=mid){
        C[t++] = B[a++];
    }
    while(b<=e){
        if(flag&1){
            if(!B[b].b){
                if(B[b].op&2){ // 查询操作，正的
                    *B[b].pans += cnt * (MAX-B[b].time) + sum;
                }else if(B[b].op&4){
                    *B[b].pans -= cnt * (MAX-B[b].time) + sum;
                }
            }
            C[t++] = B[b++];
        }else{
            if(!B[b].b){
                if(B[b].op&2){ // 查询操作，正的
                    *B[b].pans += sum - cnt * B[b].time - cnt;
                }else if(B[b].op&4){
                    *B[b].pans -= sum - cnt * B[b].time - cnt;
                }
            }
            C[t++] = B[b++];
        }
    }
    copy(C+s,C+e+1,B+s);
}

void CDQ(int s, int e, int flag){
    if(s>=e) return;
    int mid = (s+e) >> 1;
    CDQ(s, mid, flag); CDQ(mid+1, e, flag);

    int a = s, b = mid+1, t = s;
    while(a<=mid&&b<=e){
        if(A[a].y<=A[b].y){
            B[t] = A[a++];
            B[t++].b = 1;
        }else{
            B[t] = A[b++];
            B[t++].b = 0;
        }
    }
    while(a<=mid){
        B[t] = A[a++];
        B[t++].b = 1;
    }
    while(b<=e){
        B[t] = A[b++];
        B[t++].b = 0;
    }
    copy(B+s,B+e+1,A+s);
    CDQ2(s, e, flag);
}
int main(){
    //freopen("1.txt","r",stdin);
    N = getUnsigned();
    Q = getUnsigned();
    MAX = getUnsigned();
    for(int i=1;i<=N;++i){
        A[i].x = getUnsigned();
        A[i].y = getUnsigned();
        A[i].time = -(MAX - getUnsigned());
        A[i].op = 1;
    }
    //disp(N);
    QCnt = N;
    for(int t,xl,yl,xr,yr,i=1;i<=Q;++i){
        t = - getUnsigned();
        xl = getUnsigned();
        yl = getUnsigned();
        xr = getUnsigned();
        yr = getUnsigned();
        A[++QCnt].time=t;A[QCnt].x = xl-1;A[QCnt].y=yl-1;A[QCnt].op=2;A[QCnt].pans = Ans+i;
        A[++QCnt].time=t;A[QCnt].x = xl-1;A[QCnt].y=yr;A[QCnt].op=4;A[QCnt].pans = Ans+i;
        A[++QCnt].time=t;A[QCnt].x = xr;A[QCnt].y=yl-1;A[QCnt].op=4;A[QCnt].pans = Ans+i;
        A[++QCnt].time=t;A[QCnt].x = xr;A[QCnt].y=yr;A[QCnt].op=2;A[QCnt].pans = Ans+i;
    }

    sort(A+1, A+QCnt+1);
    CDQ(1,QCnt,1);

    sort(A+1, A+QCnt+1, cmp2);
    CDQ(1,QCnt,2);
    for(int i=1;i<=Q;++i)writeln(Ans[i]);
    return 0;
}

CDQ套树状数组，要离散化。

#include
using namespace std;

char *__abc147, *__xyz258, __ma369[100000];
#define __hv007() ((__abc147==__xyz258) && (__xyz258=(__abc147=__ma369)+fread(__ma369,1,100000,stdin),__abc147==__xyz258) ? EOF : *__abc147++)

int getUnsigned(){
	char ch = __hv007();
	while( ch < '0' || ch > '9' ) ch = __hv007();

	int ret = (int)(ch-'0');
	while( '0' <= ( ch = __hv007() ) && ch <= '9' ) ret = (ret<<1) + (ret<<3) + (int)(ch-'0');
	return ret;
}


typedef long long llt;

const int SIZE = 250500;
llt Cnt[SIZE], Sum[SIZE];

llt Time[SIZE];//离散化数组
int TIdx;//离散化用

inline int lowbit(int x){return x&-x;}
void modify(llt *a, int i, llt x){while(i <= TIdx) a[i] += x, i += lowbit(i);return;}
llt query(llt *a, int i){llt res = 0;while(i) res += a[i], i -= lowbit(i); return res;}


int N, Q, QCnt;
llt MAX, Ans[SIZE];
struct cdq_t{
    int x, y, op;//op代表操作类型，id代表一个询问的初始位置
    llt time, pos;//pos为离散化后的查询点/修改点
    llt *pans;
    bool operator < (const cdq_t& a)const {
        if(x!=a.x) return x < a.x;
        if(y!=a.y) return y < a.y;
        //if(time!=a.time) return time < a.time; // 这一句不能加
        return op < a.op;//如果x坐标相同，插入要优先于查询
    }
}A[SIZE], B[SIZE];


void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s+e)>>1;
    CDQ(s, mid); CDQ(mid+1, e);

    int a = s, b = mid+1, t = s;
    while(a <= mid && b <= e){
        if(A[a].y <= A[b].y){
            if(A[a].op == -2){//加入星星
                modify(Cnt, A[a].pos, 1);
                modify(Sum, A[a].pos, A[a].time);
            }
            B[t++] = A[a++];
        }
        else{
            if(A[b].op != -2){
                llt v = query(Sum, TIdx);//总的初始价值
                llt cnt1 = query(Cnt, TIdx);//总的星星
                llt cnt2 = query(Cnt, A[b].pos);//在[0, MAX-time]的星星
                //Ans[A[b].id] += A[b].op*( v + cnt1*(A[b].time) - (cnt1 - cnt2)*(MAX+1) );
                //*A[b].pans += A[b].op*( v + cnt1*(A[b].time) - (cnt1 - cnt2)*(MAX+1) );
                *A[b].pans += A[b].op * (v + cnt2*MAX-cnt1*A[b].time-(cnt1-cnt2));
            }
            B[t++] = A[b++];
        }
    }
    while(b <= e){//先把查询处理完
        if(A[b].op != -2){
            llt v = query(Sum, TIdx);
            llt cnt1 = query(Cnt, TIdx), cnt2 = query(Cnt, A[b].pos);
            //Ans[A[b].id] += A[b].op*( v + cnt1*(A[b].time) - (cnt1 - cnt2)*(MAX+1) );
            //*A[b].pans += A[b].op*( v + cnt1*(A[b].time) - (cnt1 - cnt2)*(MAX+1) );
            *A[b].pans += A[b].op * (v + cnt2*MAX-cnt1*A[b].time-(cnt1-cnt2));
        }
        B[t++] = A[b++];
    }
    for(int i = s; i < a; ++i){//删除之前的更改
        if(A[i].op == -2){
            modify(Cnt, A[i].pos, -1);
            modify(Sum, A[i].pos, -A[i].time);
        }
    }
    while(a <= mid) B[t++] = A[a++];//再把左边剩余的处理完
    copy(B+s, B+e+1, A+s);
}


int main(){
    //freopen("1.txt","r",stdin);
    N = getUnsigned();
    Q = getUnsigned();
    MAX = getUnsigned();
	TIdx = 0;
	for(int i = 1; i <= N; ++i){
        A[i].x = getUnsigned();
        A[i].y = getUnsigned();
        Time[TIdx++] = A[i].time = getUnsigned() - MAX;
        A[i].op = -2;
	}
	QCnt = N;
	for(int t,x1,y1,x2,y2,i = 1; i <= Q; ++i){
        t = getUnsigned();
        x1 = getUnsigned();
        y1 = getUnsigned();
        x2 = getUnsigned();
        y2 = getUnsigned();

        A[++QCnt].pans = Ans+i, A[QCnt].op = 1, A[QCnt].x = x1 - 1, A[QCnt].y = y1 - 1, A[QCnt].time = -t;
        A[++QCnt].pans = Ans+i, A[QCnt].op = 1, A[QCnt].x = x2, A[QCnt].y = y2, A[QCnt].time = -t;
        A[++QCnt].pans = Ans+i, A[QCnt].op = -1, A[QCnt].x = x2, A[QCnt].y = y1 - 1, A[QCnt].time = -t;
        A[++QCnt].pans = Ans+i, A[QCnt].op = -1, A[QCnt].x = x1 - 1, A[QCnt].y = y2, A[QCnt].time = -t;
        Time[TIdx++] =  - t;
	}

	sort(A+1, A+QCnt+1);
	sort(Time, Time+TIdx);
	TIdx = unique(Time,Time+TIdx) - Time;
	for(int i = 1; i <= QCnt; ++i) A[i].pos = lower_bound(Time,Time+TIdx, A[i].time) - Time + 1;
	CDQ(1, QCnt);
	for(int i = 1; i <= Q; ++i) printf("%lld\n", Ans[i]);
}

CDQ分治解法稍微深入

四维偏序

四维偏序就是在三维偏序的基础上再套一维，可以有多种组合的解法。例如CDQ套KDTree，CDQ套CDQ套树状数组，CDQ套CDQ套CDQ。如果从CDQ入手的话，一般CDQ套CDQ套树状数组较好。三重CDQ套娃速度比较慢，需要一些优化。

hdu5126，在三维空间中，两种操作

1. x,y,z: 一颗星星出现，即插入操作
2. x1,y1,z1,x2,y2,z2: 问该长方体空间内有多少个星星

很明显是一个四维偏序问题，当$T_i\le T_j,Po{s}_i\le Po{s}_j$且$i$为插入$j$为查询时对答案有影响。因为时间线天然有序，所以省了一个排序的操作，另外时刻绝不可能相同，因此也无需去重。但是显然要离散化。

#include 
using namespace std;

char *__abc147, *__xyz258, __ma369[100000];
#define __hv007() ((__abc147==__xyz258) && (__xyz258=(__abc147=__ma369)+fread(__ma369,1,100000,stdin),__abc147==__xyz258) ? EOF : *__abc147++)

int getUnsigned(){
	char ch = __hv007();
	while( ch < '0' || ch > '9' ) ch = __hv007();

	int ret = (int)(ch-'0');
	while( '0' <= ( ch = __hv007() ) && ch <= '9' ) ret = (ret<<1) + (ret<<3) + (int)(ch-'0');
	return ret;
}


typedef long long llt;
int const SIZE = 50010 * 8;

int WCnt;
int BIT[SIZE];

inline int lowbit(int x){return x & -x;}
void modify(int pos, int delta){
    for(;pos<=WCnt;pos+=lowbit(pos))BIT[pos] += delta;
}

int query(int pos){
    int ans = 0;
    for(;pos;pos-=lowbit(pos)) ans += BIT[pos];
    return ans;
}

struct cdq_t{
    int x, y, z;
    int op;
    int *pans;
    bool b;
}A[SIZE], B[SIZE], C[SIZE];


int Ans[SIZE], ACnt;
int N, Q, W[SIZE];

inline void mk8(int i){
    int xl = getUnsigned();
    int yl = getUnsigned();
    int zl = getUnsigned();
    int xr = getUnsigned();
    int yr = getUnsigned();
    int zr = getUnsigned();

    A[++Q].op = -1;
    A[Q].x = xl - 1;
    A[Q].y = yl - 1;
    A[Q].z = (W[WCnt++] = zl - 1);
    *(A[Q].pans = Ans + ACnt) = 0;

    A[++Q].op = 1;
    A[Q].x = xl - 1;
    A[Q].y = yl - 1;
    A[Q].z = W[WCnt++] = zr;
    *(A[Q].pans = Ans + ACnt) = 0;

    A[++Q].op = 1;
    A[Q].x = xl - 1;
    A[Q].y = yr;
    A[Q].z = zl - 1;
    *(A[Q].pans = Ans + ACnt) = 0;

    A[++Q].op = -1;
    A[Q].x = xl - 1;
    A[Q].y = yr;
    A[Q].z = zr;
    *(A[Q].pans = Ans + ACnt) = 0;

    A[++Q].op = 1;
    A[Q].x = xr;
    A[Q].y = yl - 1;
    A[Q].z = zl - 1;
    *(A[Q].pans = Ans + ACnt) = 0;

    A[++Q].op = -1;
    A[Q].x = xr;
    A[Q].y = yl - 1;
    A[Q].z = zr;
    *(A[Q].pans = Ans + ACnt) = 0;

    A[++Q].op = -1;
    A[Q].x = xr;
    A[Q].y = yr;
    A[Q].z = zl - 1;
    *(A[Q].pans = Ans + ACnt) = 0;

    A[++Q].op = 1;
    A[Q].x = xr;
    A[Q].y = yr;
    A[Q].z = zr;
    *(A[Q].pans = Ans + ACnt++) = 0;
}

void CDQ2(int s, int e){
    if(s>=e) return;

    int mid = (s + e) >> 1;
    CDQ2(s, mid); CDQ2(mid+1, e);

    int a = s, b = mid + 1, t = a;
    while(a<=mid&&b<=e){
        if(B[a].y<=B[b].y){
            if(B[a].b&&!B[a].op){
                modify(B[a].z, 1);
            }
            C[t++] = B[a++];
        }else{
            if(!B[b].b&&B[b].op){
                *B[b].pans += B[b].op * query(B[b].z);
            }
            C[t++] = B[b++];
        }
    }
    while(b<=e){
        if(!B[b].b&&B[b].op){
            *B[b].pans += B[b].op * query(B[b].z);
        }
        C[t++] = B[b++];
    }
    for(int i=s;i<a;++i){
        if(B[i].b&&!B[i].op){
            modify(B[i].z, -1);
        }
    }
    while(a<=mid){
        C[t++] = B[a++];
    }
    copy(C+s, C+e+1, B+s);
}

void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s + e) >> 1;
    CDQ(s, mid); CDQ(mid+1, e);

    int a = s, b = mid + 1, t = a;
    while(a<=mid&&b<=e){
        if(A[a].x<=A[b].x){
            B[t] = A[a++];
            B[t++].b = 1;
        }else{
            B[t] = A[b++];
            B[t++].b = 0;
        }
    }
    while(a<=mid){
        B[t] = A[a++];
        B[t++].b = 1;
    }
    while(b<=e){
        B[t] = A[b++];
        B[t++].b = 0;
    }

    copy(B+s, B+e+1, A+s);
    CDQ2(s, e);
}

int main(){
    //freopen("1.txt","r",stdin);
    int nofkase = getUnsigned();
    while(nofkase--){
        N = getUnsigned();
        ACnt = WCnt = Q = 0;

        for(int cmd,i=1;i<=N;++i){
            cmd = getUnsigned();
            if(1==cmd){
                A[++Q].x = getUnsigned();
                A[Q].y = getUnsigned();
                W[WCnt++] = A[Q].z = getUnsigned();
                A[Q].op = 0;

            }else{ // 变成8个操作
                mk8(i);
            }
        }

        /// 离散化z坐标
        sort(W, W+WCnt);
        WCnt = unique(W, W+WCnt) - W;
        for(int i=1;i<=Q;++i){
            A[i].z = lower_bound(W, W+WCnt, A[i].z) - W + 1;
        }

        CDQ(1, Q);
        for(int i=0;i<ACnt;++i)printf("%d\n", Ans[i]);
    }
    return 0;
}

递归归并的顺序

从归并排序以及逆序对而来的分治框架，对某些题目而言是不适合的。考虑洛谷3769，四维空间中每一维坐标均不降的最长路径。很明显，当$x_i<x_j,y_i<y_j,z_i<z_j,w_i<w_j$时，$D_i$可能对$D_j$有贡献，所以这是一个四维偏序的问题。
不过这个题目的答案贡献与前面的基础题都不一样。之前的题目都是加法，所以先加后加无所谓。所以对于右段的点，是先计算内部的贡献，再计算左段对右段的贡献。假设右段有$b_1,b_2$两个点，先计算$b_1$对$b_2$的贡献，再计算左段的点对$b_2$的贡献，由于这个贡献是累加无时效性的，所以这样做没有问题。
但是这道题的$DP$方程是$D_j=max\{D_i,所有满足条件的i\}$，所以必须先计算完$i$，再计算$j$，否则答案可能会有错误。所以如果先计算了$b_1$对$b_2$的影响，这个时候由于左段对$b_1$的影响还没有计算出来，会导致$b_2$的答案并不正确。因此，对于这一类题目，必须先计算左段，再计算左右之间，最后计算右段。相应的也就没有办法进行归并了，需要直接$sort$。
既然要直接$sor$t，把归并用的临时数组也去掉，就只用一个数组，在每次归并前按当时维度进行排序，然后进行归并统计答案即可。注意要去重和离散化。

#include 
using namespace std;

typedef long long llt;
int const SIZE = 50010;

int WCnt;
int BIT[SIZE];

inline int lowbit(int x){return x & -x;}
void modify(int pos, int delta){
    for(;pos<=WCnt;pos+=lowbit(pos))BIT[pos] = max(BIT[pos], delta);
}
void modify(int pos){
    for(;pos<=WCnt;pos+=lowbit(pos))BIT[pos] = 0;
}
int query(int pos){
    int ans = 0;
    for(;pos;pos-=lowbit(pos)) ans = max(ans, BIT[pos]);
    return ans;
}
struct cdq_t{
    int x,y,z,w;
    int cnt;
    int *pans;
    bool b;
    void get(){
        scanf("%d%d%d%d",&x,&y,&z,&w);
    }
    bool operator < (const cdq_t &rhs)const{
        if(x!=rhs.x) return x < rhs.x;
        if(y!=rhs.y) return y < rhs.y;
        if(z!=rhs.z) return z < rhs.z;
        return w < rhs.w;
    }
    bool operator == (const cdq_t &rhs)const{
        return x==rhs.x&&y==rhs.y&&z==rhs.z&&w==rhs.w;
    }
}A[SIZE];

bool cmp2(const cdq_t &lhs, const cdq_t &rhs){
    if(lhs.y!=rhs.y) return lhs.y < rhs.y;
    if(lhs.x!=rhs.x) return lhs.x < rhs.x;
    if(lhs.z!=rhs.z) return lhs.z < rhs.z;
    return lhs.w < rhs.w;
}

bool cmp3(const cdq_t &lhs, const cdq_t &rhs){
    if(lhs.z!=rhs.z) return lhs.z < rhs.z;
    if(lhs.x!=rhs.x) return lhs.x < rhs.x;
    if(lhs.y!=rhs.y) return lhs.y < rhs.y;
    return lhs.w < rhs.w;
}


int Ans[SIZE];
int N, W[SIZE];

void CDQ2(int s, int e){
    if(s>=e) return;

    int mid = (s + e) >> 1;
    CDQ2(s, mid);

    sort(A+s,A+mid+1,cmp3); // 两段分别按第三维坐标排序
    sort(A+mid+1,A+e+1,cmp3);

    int a = s, b = mid+1, t = s;
    while(a<=mid&&b<=e){
        if(A[a].z<=A[b].z){
            if(A[a].b){
                modify(A[a].w, *A[a].pans);
            }
            ++a;
        }else{
            if(!A[b].b){
                *A[b].pans = max(*A[b].pans, query(A[b].w) + A[b].cnt);
            }
            ++b;
        }
    }
    while(b<=e){
        if(!A[b].b){
            *A[b].pans = max(*A[b].pans, query(A[b].w) + A[b].cnt);
        }
        ++b;
    }
    for(int i=s;i<a;++i){
        if(A[i].b){
            modify(A[i].w);
        }
    }

    sort(A+mid+1, A+e+1, cmp2);
    CDQ2(mid+1, e);
}

void CDQ(int s, int e){
    if(s>=e) return;

    int mid = (s + e) >> 1;
    CDQ(s, mid);

    for(int i=s;i<=e;++i){
        A[i].b = i <= mid ? 1 : 0;
    }
    sort(A+s, A+e+1, cmp2); // 进入第二层CDQ前，要按第二维坐标排序
    CDQ2(s, e);

    sort(A+s, A+e+1); // 再排回来
    CDQ(mid+1, e);
}

int main(){
    //freopen("1.txt","r",stdin);
    scanf("%d", &N);
    for(int i=1;i<=N;++i){
        A[i].get();
        W[i] = A[i].w;
        A[i].cnt = 1;
    }

    sort(W+1, W+N+1);
    WCnt = unique(W+1, W+N+1) - W - 1;

    sort(A+1, A+N+1);
    int k = 1;
    for(int i=2;i<=N;++i){
        if(A[k]==A[i]){
            ++A[k].cnt;
        }else{
            A[++k] = A[i];
        }
    }
    N = k;
    for(int i=1;i<=N;++i){
        A[i].w = lower_bound(W+1,W+WCnt+1,A[i].w) - W;
        *(A[i].pans = Ans + i) = A[i].cnt;
    }
    CDQ(1, N);
    cout<<*max_element(Ans+1, Ans+N+1)<<endl;
    return 0;
}