支配树与Lengauer-Tarjan算法

支配点

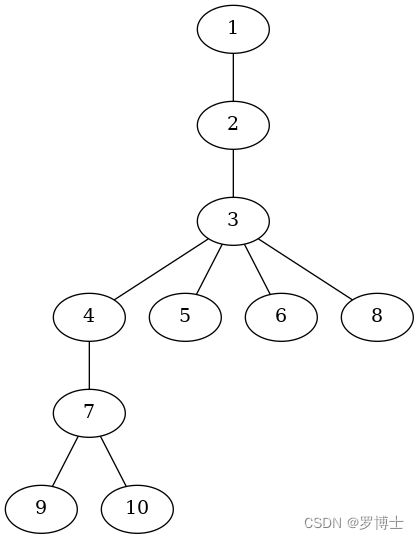
在一个有向图中，确定$S$作为起点。对某个点$x$而言，如果点$y$是$x$的支配点，则从$S$到$x$的任意路径均必须经过$y$。显然支配点可能不止一个。但如果将$x$的最近支配点到$x$连一条边，则会形成一个树形结构，称之为支配树。

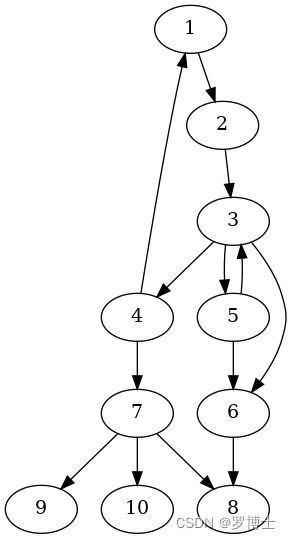
假设有图

digraph demo{
    1 -> {2}
    2 -> {3}
    3 -> {4, 5, 6}
    4 -> {1, 7}
    5 -> {3, 6}
    6 -> {8}
    7 -> {8, 9, 10}
}

且可视化如下

则其支配树是

dfs序与半支配点

从$S$开始做一个深搜，依次进入的点的顺序即为dfs序。上图的dfs序为

1 2 3 4 7 8 9 10 5 6 

dfs序显然不是唯一的，一般而言，书面表示还会尽量写成升序形式以方便阅读。

$x$节点的半支配点$y$是指: 1. 从$y$到$x$有一条路径，其中间点（不包括$x$和$y$本身）的$dfs$序均大于$x$的$dfs$序；2. 且$y$的$dfs$序是所有满足上述条件的点中最小的那个。半支配点显然是唯一的。

在上述例子中，$\{1,2,3,4,5\}$是一个强连通分量，考虑其到8的路径，显然只有

3 -> 6 -> 8
3 -> 5 -> 6 -> 8
5 -> 6 -> 8

这三条路径满足条件1，而其中节点$3$是$dfs$序最小的。因此$8$的半支配点是$3$。

根据半支配点的定义，很容易写出一个递归的写法：

1. 对于$x$节点的前驱$y$，如果$DF{N}_y<DF{N}_x$，则$y$是$x$的半支配点候选；
2. 否则，考虑$y$的所有$dfs$序大于$x$的祖先节点，这些祖先节点的半支配点是x的半支配点候选。

当然暴力维护是不行的，需要安排好迭代顺序与数据结构。

令$Sdo{m}_i$是i的当前的半支配点，即当前能够找到的符合条件的dfs序最小的点；$m{n}_i$表示节点i的祖先中dfs序最小的节点，$un{i}_i$表示。

确定支配点

假设$y$是$x$的半支配点，同时$u$是$y$到$x$路径上的一个点，$u$的半支配点$v$的$dfs$序是所有$y$到$x$路径上点中最小的，则$x$的支配点有两种情况：

1. $v==y$, 则$x$的支配点就是$y$；
2. $DF{N}_v<DF{N}_y$，则$x$的支配点就是$u$的支配点。

可以证明，不会证明。

算法与代码

下述算法是核心算法，用于求取半支配点以及部分支配点（第一种情况）。

for i in range(N, 1): # 按照dfs序的逆序遍历
    u = Ord[i] # 排名第i位的节点记作u
    for v in ig[u]: # 遍历u的入点
        uni_query(v) # 对v做一个并查集的查询，
        if Dfn[Sdom[mn[v]]] < Dfn[Sdom[u]]: # mn[v]表示v的祖先中半支配点dfs序最小的那个祖先
            Sdom[u] = Sdom[mn[v]] # 更新半支配点
	uni[u] = Parent[u] # 并查集合并
	SdomTree[Sdom[u]].append(u) # Sdom[u]到u引一条边
	u = Parent[u]
	for v in SdomTree[u]:
		uni_query(v) # 再次做一个查询，主要是为了更新uni[v]
		# u是v的半支配点，mn[v]是v的半支配点dfs序最小的那个祖先，如果if成立就是上文中的第一种情况
		# 否则，暂时将Idom[v]记作mn[v]
		Idom[v] = u if u == Sdom[mn[v]] else mn[v]

洛谷支配树模板题代码如下。

#include 
using namespace std;

struct DominatorTree_Lengauer_Tarjan{

using vi = vector<int>;
using vvi = vector<vi>;

vvi g; // 1-indexed
vvi ig;

void init(int n){
    g.assign(n + 1, vi());
	ig.assign(n + 1, vi());
}

void mkEdge(int a, int b){
	g[a].push_back(b);
	ig[b].push_back(a);
}

int S;
vi Dfn; // Dfn[i]表示节点i的dfs序
vi Ord; // Ord[i]表示排名第i位的节点
vi Parent; // Parent[i]表示深搜树上i节点的父节点
int Stamp; 

vi uni; // 带权并查集的father数组
vi mn;  // mn[i]表示i的所有祖先中，半支配点的dfs序最小的那个祖先
vi Sdom; // Sdom[i]表示i的半支配点
vi Idom; // Idom[i]表示i的直接支配点

vvi SdomTree;

void Lengauer_Tarjan(int s){
	int n = this->g.size() - 1;

    /// 确定dfs序
	Dfn.assign(this->g.size(), Stamp = 0);
	Ord.assign(this->g.size(), 0);
	Parent.assign(this->g.size(), 0);
	dfs(S = s);

	/// 求解半支配点与支配点的中间答案
	Sdom.assign(this->g.size(), 0);
	uni.assign(this->g.size(), 0);
	mn.assign(this->g.size(), 0);
	SdomTree.assign(this->g.size(), vi());
	Idom.assign(this->g.size(), 0);
	calcSdom();

    /// 最后确定支配点
	for(int i=2;i<=n;++i){
		int u = Ord[i];
		if(Idom[u] ^ Sdom[u]){
			Idom[u] = Idom[Idom[u]];
		}
	}
	return;
}

void dfs(int u){
	Ord[Dfn[u] = ++Stamp] = u;
	for(auto v : g[u]){
		if(0 == Dfn[v]){
			Parent[v] = u;
			dfs(v);
		}		
	}
	return;
}

void calcSdom(){
	int n = this->g.size() - 1;
	for(int i=1;i<=n;++i) Sdom[i] = mn[i] = uni[i] = i;
	for(int i=n;i>=2;--i){
		int u = Ord[i]; // 排名第i位的节点是u
		for(int v : ig[u]){
			if(0 == Dfn[v]) continue;
			uni_query(v);
			if(Dfn[Sdom[mn[v]]] < Dfn[Sdom[u]]){
				Sdom[u] = Sdom[mn[v]];
			} 
		}
		uni[u] = Parent[u]; // 将u向上合并
		SdomTree[Sdom[u]].push_back(u);
		for(int v : SdomTree[u = Parent[u]]){
			uni_query(v);
			Idom[v] = (u == Sdom[mn[v]]) ? u : mn[v]; 
		}
		SdomTree[u].clear();
	}
	return;
}

/// 带权并查集的find操作
int uni_query(int u){
	if(u == uni[u]) return u;
	int ans = uni_query(uni[u]);
	/// mn[u]是通过mn[uni[u]]计算出来的
	if(Dfn[Sdom[mn[uni[u]]]] < Dfn[Sdom[mn[u]]]) mn[u] = mn[uni[u]];
	return uni[u] = ans;
}

};

int N, M;
DominatorTree_Lengauer_Tarjan D;

int main(){
#ifndef ONLINE_JUDGE
    freopen("1.txt", "r", stdin);
#endif
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin >> N >> M;
	D.init(N);
	for(int a,b,i=0;i<M;++i){
        cin >> a >> b;
		D.mkEdge(a, b);
	}
	D.Lengauer_Tarjan(1);
    vector<int> ans(N+1, 0);
	for(int i=N;i>=2;--i) ans[D.Idom[D.Ord[i]]] += ++ans[D.Ord[i]];
	++ans[1];
	for(int i=1;i<=N;++i) cout << ans[i] << " "; cout << endl;
    return 0; 
}